Файл: Лабораторная работа 2 Кафедра механики По дисциплине Сопротивление материалов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 25
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»
Лабораторная работа № 2
Кафедра механики
По дисциплине: Сопротивление материалов
(наименование учебной дисциплины согласно учебному плану)
Тема работы: Определение модуля упругости и коэффициента Пуассона
Автор: студент гр. ТПП-19
(шифр группы) (подпись) (Ф.И.О.)
Оценка:
Проверил: доцент __________ П
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
 2021
2021Цель работы: изучение способа измерения модуля упругости и коэффициента Пуассона, определение упругих констант стали.
Краткие теоретические сведения
При растяжении стержня в нем возникают продольные напряжения ZИпродольные Z и поперечные X деформации.
При растягивающих усилиях, соответствующих напряжениям, не превышающим предел текучести, продольные напряжения и деформации связаны соотношением, называемым законом Гука:
E,
где Е — модуль упругости, который также называют модулем Юнга.
Кроме продольных деформаций, в стержне возникают деформации в плоскости, перпендикулярной его оси (поперечные деформации), величину:
= εХ /εZ –
называют коэффициентом Пуассона.
При нагружении стержня в пределах упругой области коэффициент Пуассона является постоянной величиной и связь между продольными и поперечными деформациями в стержне линейна.
Таблица геометрических параметров
Таблица 1 – Геометрические параметры
| t,мм | b,мм | l,мм | F,мм2 |
| 3,0 | 40,0 | 40,0 | 377 |
Протокол испытаний
Таблица 2 – Протокол испытаний
| Измеренные величины | Рассчитанные величины | |||||||
| P,кН | ∆z,мм | ∆x,мм | εzтр*10-6 | εхтр, 10-6 | σ,МПа | εz, 10-6 | εx, 10-6 | |
| 3,6 | 0,006 | -0,002 | 117 | -36 | 9,55 | 150 | -50 | |
| 6,2 | 0,010 | -0,002 | 212 | -62 | 16,45 | 250 | -75 | |
| 9,1 | 0,016 | -0,004 | 325 | -94 | 24,14 | 400 | -100 | |
| 12,2 | 0,02 | -0,005 | 445 | -129 | 32,36 | 500 | -125 | |
| 15,3 | 0,024 | -0,006 | 565 | -163 | 40,58 | 600 | -150 | |
| 18,3 | 0,029 | -0,008 | 685 | -197 | 48,54 | 725 | -200 | |
| 21,2 | 0,033 | -0,009 | 802 | -231 | 56,23 | 825 | -225 | |
| 24,1 | 0,038 | -0,010 | 917 | -265 | 63,93 | 950 | -250 | |
| 27,1 | 0,042 | -0,011 | 1042 | -301 | 71,88 | 1050 | -275 | |
Вычисления
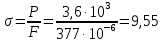 МПа.
МПа.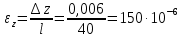 .
.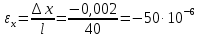 .
.Из рисунка 1 мы видим, что модуль упругости равен:
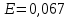 .
.По формуле получим коэффициент Пуассона по рисунку 2:
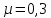 .
.Графический материал
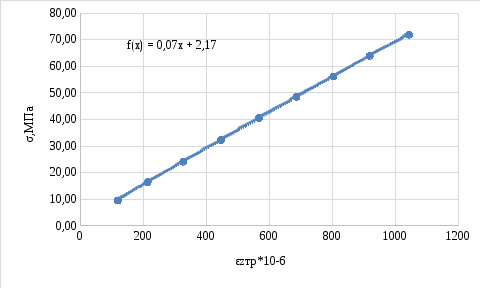
Рисунок 1 – Зависимость σ(εzтр*10-6)
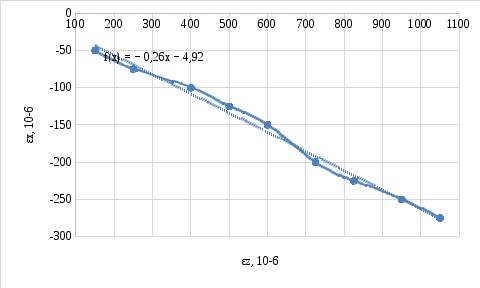
Рисунок 2 – εХ(εZ)
Вывод
В данной работе мы опытным путем определили величину модуля упругости Ε и коэффициент Пуассона μ и сравнить полученные результаты со справочными данными.