Файл: Контрольная работа по дисциплине Прогнозирование.docx

министерство науки и высшего образования российской федерации

федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский Нижегородский государственный университет им. Н.И. Лобачевского»

Институт экономики и предпринимательства

Кафедра информационных технологий и инструментальных методов в экономике


Контрольная работа

по дисциплине «Прогнозирование»


Работу выполнил студентка

Группы: 35193-Ээ-3ук

Ю.В.Миронова

(подпись)

Номер зачетной книжки: s19351978

Курс, группа, Фамилия И.О.

Нижний Новгород,

2023
Задача 1. Прогнозирование с помощью среднего абсолютного прироста

Условие:Данные таблицы описывают изменение, процентной ставки банка в течение семи кварталов

Текущий номер квартала, t	1	2	3	4	5	6	7
Процентная ставка банка, уt %	16,37	17	17	17	17,5	17,5	17,9

Требуется:

1. 
   рассчитать прогнозное значение процентной ставки банка в восьмом квартале с помощью среднего абсолютного прироста.
   
2. 
   обосновать правомерность использования среднего абсолютного прироста для получения прогнозного значения процентной ставки в восьмом квартале;
   

---

Решение:

Начертите таблицу и рассчитайте в ней абсолютный цепной прирост и средний абсолютный прирост

Текущий номер квартала, t	1	2	3	4	5	6	7	8
Процентная ставка банка, уt %	16,37	17	17	17	17,5	17,5	17,9	16,37
Абсолютный цепной прирост	×	0,73	0	0	0,5	0	0,4	×
Средний абсолютный прирост	0,26

1.Рассчитайте прогнозное значение процентной ставки банка. Занесите его в таблицу.

Абсолютный прирост (Δу) характеризует размер увеличения (или уменьшения) уровня ряда за определенный промежуток времени. Он равен разности двух сравниваемых уровней и выражает абсолютную скорость роста:

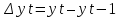, где

y_t - текущий уровень ряда динамики;

y_t-1 - предыдущий уровень ряда динамики.

1. 
   Δy₂ = 17 – 16,37 = 0,73%;
   
2. 
   Δy₃ = 17 – 17 = 0%;
   
3. 
   Δy₄ = 17 – 17 = 0%
   
4. 
   Δy₅ = 17,5 – 17 = 0,5%;
   
5. 
   Δy₆ = 17,5 – 17,5 = 0%;
   
6. 
   Δy₇ = 17,9 – 17,5 = 0,4%
   

Средний абсолютный прирост показывает, на сколько единиц увеличивался или уменьшался уровень по сравнению с предыдущим в среднем за единицу времени. Средний абсолютный прирост характеризует среднюю абсолютную скорость роста (или снижения) уровня и всегда является интервальным показателем:

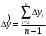, где

n - длина временного ряда.



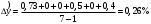
Прогноз на 8 квартал:

у₈ = 17,9 + 0,26 = 18,16%

2.Обоснуйте применение среднего абсолютного прироста для прогнозирования значения процентной ставки.

Очевидно, что такой подход к получению прогнозируемого значения является правильным, если характер развития близок к линейному. Примерно одинаковые значения абсолютных приращений строки могут свидетельствовать о такой равномерности развития. При этом значения абсолютных приращений цепочки не сильно отклоняются друг от друга, поэтому для прогноза можно использовать среднее абсолютное приращение.

---

Ответ:прогноз на 8 квартал 0,26%.

Условие:В таблице представлены данные об изменении среднего реального располагаемого дохода за 16 лет у домохозяйств. Требуется:

1. 
   провести сглаживание временного ряда, используя пятилетнюю простую скользящую среднюю;
   
2. 
   провести сглаживание временного ряда, используя пятилетнюю взвешенную скользящую среднюю (выравнивание проводить по полиному второго порядка).
   
3. 
   восстановить потерянные уровни для простой скользящей средней.
   
4. 
   построить график, на который должны быть нанесены три ломаные линии.
   

Текущий номер года, t	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Средний реальный располагаемый доход, тыс. руб, Yt	14,82	21,66	19,38	20,52	15,96	22,8	21,66	27,36	36,48	36,8	38,76	43,1	40,74	41,04	45,6	39,9

Решение:

1. Провестисглаживаниевременногоряда,используяпятилетнююпростуюскользящуюсреднюю:

a) Определяют длину интервала сглаживания L. При этом надо иметь в виду, что чем

---

шире интервал сглаживания, тем в большей степени поглощаются колебания, и тенденция развития носит более плавный, сглаженный характер. Чем сильнее колебания, тем шире должен быть интервал сглаживания.

b) Разбивают весь период наблюдений на участки, при этом интервал сглаживания «скользит» по ряду с шагом, равным L.

c) Рассчитывают средние арифметические из уровней ряда, образующих каждый участок, по формуле:



d) Заменяют фактические значения ряда, стоящие в центре каждого участка, на соответствующие средние значения.

Пример: расчёт скользящей средней Y₃:



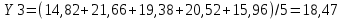
2. Алгоритм сглаживания по взвешенной скользящей средней тот же, что и для простой скользящей средней, за исключением 3 шага. Вычисляют средневзвешенную, используя формулу:



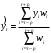
Веса отражены в таблице:

Длина интервала сглаживания	t - 2	t - 1	t	t + 1	t + 2	Сумма весов
L = 5	-3	12	17	12	-3	35

Пример:

Y₃ = (14, 82*(-3) + 21, 66*12 + 19, 38*17 + 20, 52*12 + 15, 96*(-3))/35 = 21, 24.

t	Yt	Простая скользящая средняя при L = 5	Взвешенная скользящая средняя при L = 5	Абсолютные приросты Исходный ряд	Абсолютные приросты Простая СС	Абсолютные приросты Взвешенная СС
1	2	Графа 3	Графа 4	Графа 5	Графа 6	Графа 7
1	14,82	13,91	16,68
2	21,66	16,19	18,96	6,84	2,28	2,28
3	19,38	18,47	21,24	-2,28	2,28	2,28
4	20,52	20,06	18,27	1,14	1,60	-2,96
5	15,96	20,06	19,09	-4,56	0,00	0,81
6	22,80	21,66	19,87	6,84	1,60	0,78
7	21,66	24,85	23,22	-1,14	3,19	3,35
8	27,36	29,02	28,11	5,70	4,17	4,89
9	36,48	32,21	34,54	9,12	3,19	6,42
10	36,80	36,50	37,63	0,32	4,29	3,09
11	38,76	39,18	39,60	1,96	2,68	1,97
12	43,10	40,09	41,52	4,34	0,91	1,92
13	40,74	41,85	41,41	-2,36	1,76	-0,11
14	41,04	42,08	42,42	0,30	0,23	1,02
15	45,60	41,51	41,85	4,56	-0,57	-0,57
16	39,90	40,94	41,28	-5,70	-0,57	-0,57

---

3. Восстановление потерянных уровней для простой средней:

А. вычислить средний абсолютный прирост на первом (последнем) активном участке;

Б. получить сглаженные значения в конце временного ряда путем последовательного вычитания (прибавления) среднего абсолютного прироста к последнему сглаженному значению.

2.1. Простая средняя.

Вычисление среднего абсолютного прироста в начале ряда.

t	Yt	Yt пр	Абсолютный прирост (Yt – Yt-1)	Восстановление уровней ряда
1	14,82	×	×	13,91
2	21,66	×	6,84	16,19
3	19,38	18,47	-2,28	×
Средний абсолютный прирост			2,28	×

Вычисление среднего абсолютного прироста в конце ряда:

t	Yt	Yt пр		Абсолютный прирост (Yt – Yt-1)		Восстановление уровней ряда
14	41,04	42,08		×		×
15	45,6	×		4,56		41,51
16	39,9	×		-5,7		40,94
Средний абсолютный прирост			-0,57		×

2.2. Взвешенная средняя

Вычисление среднего абсолютного прироста в начале ряда.

t	Yt	Yt пр	Абсолютный прирост (Yt – Yt-1)	Восстановление уровней ряда
1	14,82	×	×	16,68
2	21,66	×	6,84	18,96
3	19,38	21,24	-2,28	×
Средний абсолютный прирост			2,28	×

---