Файл: Гидравлика и нефтегазовая гидромеханика.docx

Физический и энергетический смысл уравнения Бернулли заключается в постоянстве полной удельной энергии вдоль элементарной струйки идеальной жидкости.

Уравнение Бернулли отражает закон сохранения механической энергии для идеальной несжимаемой жидкости.

Уравнение Бернулли для потока реальной вязкой жидкости

Если на участке между расчетными сечениями не совершается механическая работа, а движение является установившимся, без притока и отбора жидкости, и сама жидкость является несжимаемой, то для потока будут справедливы зависимости:

Н₁=Н₂ + Δh_{1 - 2}
_z1 + p₁/ρg + V₁²/2g = z₂ + p₂/ρg + V₂²/2g + Δh_{1 - 2}

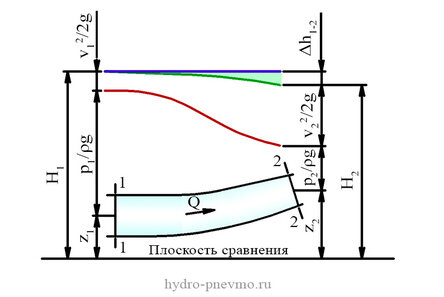
Уравнение Бернулли устанавливает связь между полными напорами потока жидкости на участке ограниченными сечениями 1-1 и 2-2. В соответствии с уравнением Бернулли полный напор потока Hi уменьшается от сечения 1-1 к сечению 2-2 на величину потерь напора (энергии) h_{1 - 2}, вызванных гидравлическими сопротивлениями участка.

Иллюстрация уравнения Бернулли

Для иллюстрации закона Бернулли на координатной плоскости, совмещенной с принципиальной гидравлической схемой системы изображают напорную и пьезометрическую линии.

Уравнение Бернулли для горизонтальной трубы

Для горизонтальных трубопроводов и силовых гидроприоводов, в которых пьезометрический набор существенно превышает геометрический удобна следующая форма записи уравнения Бернулли:

p₁ + ρV₁² = p₂ + ρV₂² + Δp₁^о

8.Режимы течения: ламинарный и турбулентный, число Ренольдтца.
Имеют место два различных по своему характеру режима движения жидкости: ламинарный и турбулентный.

При ламинарном режиме жидкость движется слоями без поперечного перемешивания, причем пульсации скорости и давления отсутствуют.

При турбулентном режиме слоистость нарушается, движение жидкости сопровождается перемешиванием и пульсациями скорости и давления.

Число Рейнольдса

Критерием для определения режима движения является безразмерное число Рейнольдса. Для труб круглого сечения число Рейнольдса определяется по формуле:

Re = υ·d/ν;

- для потоков произвольного поперечного сечения

Re_Rг = υ·R_г/ν;

или

Re_Rг = υ·D_г/ν;

где υ — средняя скорость жидкости; d — диаметр трубы; R_г— гидравлический радиус; D_г

— гидравлический диаметр; ν — кинематический коэффициент вязкости жидкости.

Режим будет ламинарным, если

Re < Re_кр;

Re_R< Re_Rкр,

и турбулентным, если

Re > Re_кр;

Re_R> Re_Rкр,

В выражениях приведенных выше Re_кр и Re_Rкр — критические числа Рейнольдса, для круглых труб обычно принимаемые равными соответственно 2320 и 580. В таблице приведены ориентировочные значения Re_кр для некруглых каналов и некоторых гидроагрегатов, при этом число Рейнольдса определено по формуле Re_Rг = υ·D_г/ν.

Для изогнутых каналов (витков), вращающихся вокруг внешней оси 0—0 (следующий рисунок), согласно исследованиям Ю. В. Квитковского и К. И. Толчеева, критическое число Рейнольдса получается несколько большим, чем для прямых труб.

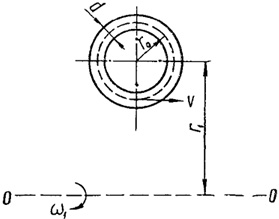
9. Определение потерь в трубопроводе (Дарси).
Линейные потери.Основной формулой линейных потерь, наиболее полно вскрывающей их суть, является формула Дарси – Вейсбаха:

где

- коэффициент гидравлического трения, он зависит от режима движения жидкости и относительной шероховатости, т.е.

;

- соответственно длина и диаметр трубопровода;

- скорость движения жидкости.

Формула является универсальной. По ней можно подсчитать линейные потери в трубопроводах любого назначения, но в настоящее время этой формулой пользуются при расчете объемного гидравлического привода.

при расчете водопроводных систем широко используются табличные методы. Так линейные потери можно определить по формуле

где

- гидравлический уклон, т.е. потери, приходящиеся на единицу длины трубопровода, берется из таблиц в зависимости от материала трубопровода, его диаметра и расхода; l - длина расчетного участка трубопровода.

Линейные потери водопроводных систем определяются так же по зависимости

где l - длина расчетного участка; Q - расход по участку; К - расходная характеристика, берется из таблиц в зависимости от материала трубопровода и его диаметра.

Рассмотрим особенности расчета безнапорных систем, каковыми являются каналы, лотки и т.п. устройства.

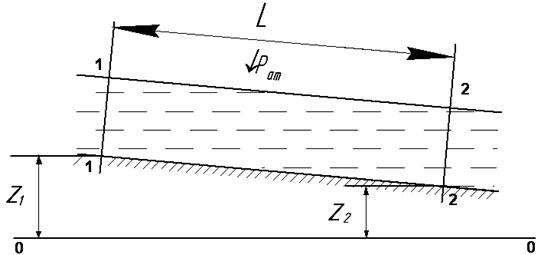
При равномерном движении жидкости в подобных системах уравнение Бернулли для потока реальной жидкости, составленное для сечений 1-1 и 2-2 имеет вид

,

т.е. разница геометрических напоров затрачивается на преодоление линейных потерь. Таким образомт движение жидкости обеспечивается наличием гидравлического уклона i, который в данном случае равен геометрическому:

.

Поэтому при проектировании каналов большой протяженности используют естественный уклон местности и в этом случае определяют пропускную способность канала и его размеры по формуле Шези:

где

- живое сечение канала; R - гидравлический радиус; С - коэффициент Шези, который зависит от гидравлического радиуса и коэффициента шероховатости.

Коэффициент Шези берется из таблиц или определяется по формулам, например, по формуле Маннинга

.

При необходимости решаются и другие задачи.

Местные потери.

Для их определения пользуются единственной формулой

где

- коэффициент местного сопротивления, берется из таблиц и графиков, вычисляется по специальным формулам в зависимости от вида местного сопротивления; V - скорость движения жидкости в трубопроводе, где установлено местное сопротивление.

10.Расчет простого трубопровода.

Простым называют трубопровод, состоящий из одной линии труб постоянного сечения (не имеет ответвлений) с постоянным расходом по длине трубопровода.

Всякие другие трубопроводы называются сложными.

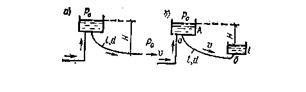
уравнение Бернулли, записанное для сечений на поверхности воды в резервуаре и на выходы из трубы, имеет вид:

Пренебрегая величиной

(очень малой по сравнению с другими членами уравнения) и обозначая z₀-z=H, приводим уравнение Бернулли к виду:

При истечении под уровень получим аналогично:

.

В этом уравнении в отличие от предыдущего местные сопротивления оценены двумя слагаемыми

. Первое слагаемое так же, как и в предыдущем случае, учитывает потери напора на протяжении трубопровода, начиная от выхода из резервуара А в трубу (точка а) и до конца трубы (точка б), за исключением потерь напора на выход в резервуаре В, которые оценены вторым слагаемым.

По аналогии с первым случаем, пренебрегая величиной