ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 168
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
При вычислении учтена четность функции Гаусса, а ее значение взято из прил.1.
Пример 9. Вероятность изготовления стандартной детали на автоматическом станке равна 0,8. Найти вероятность того, что среди 100 деталей будет от 68 до 90 стандартных деталей.
Решение. Здесь испытание состоит в проверке, является ли каждая деталь стандартной. Так как вероятность обнаружения стандартной детали в каждом опыте постоянна и равна 0,8, то по условию задачи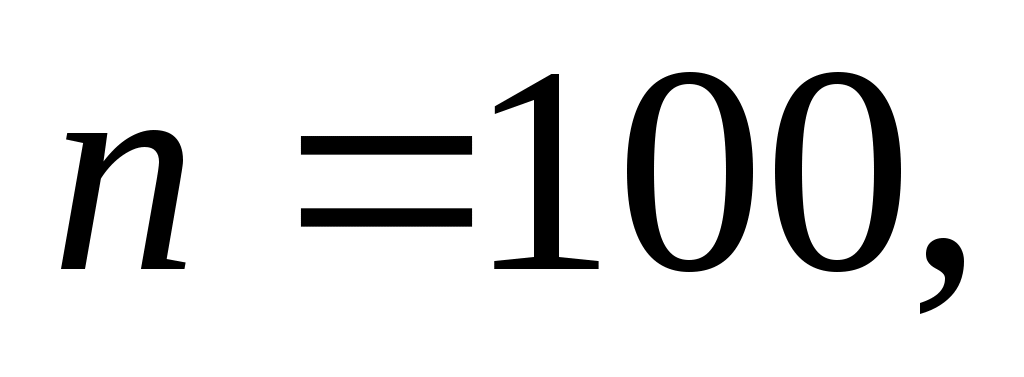
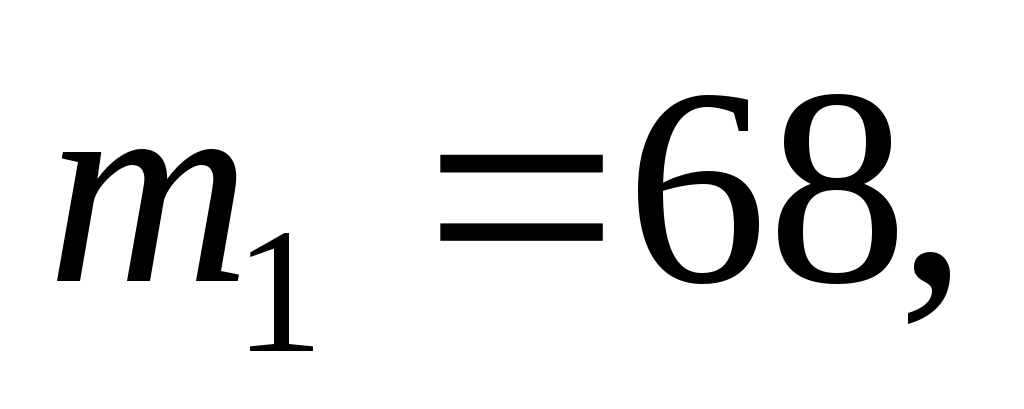
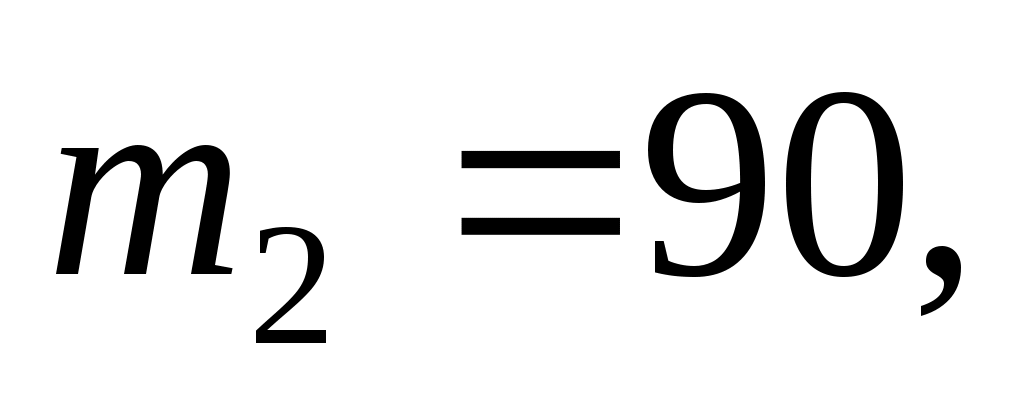
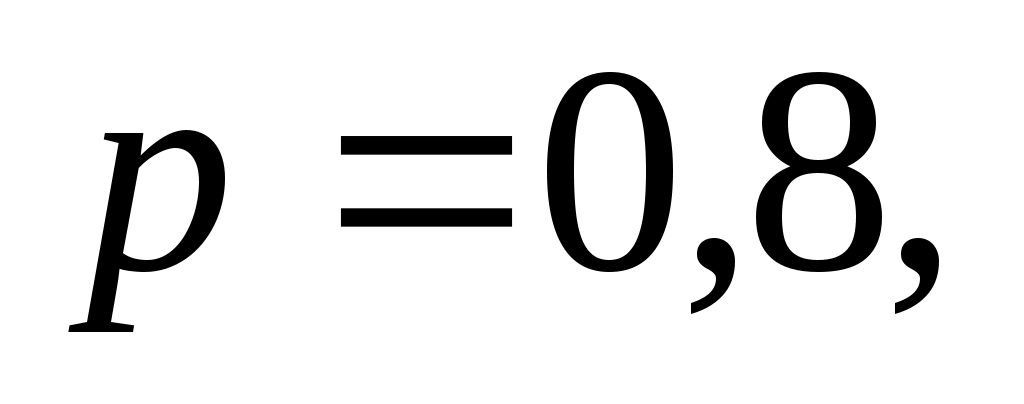
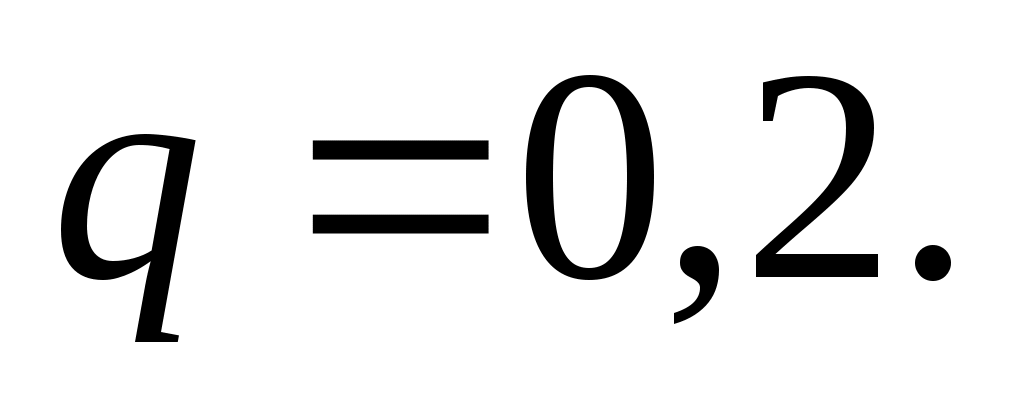 Согласно интегральной теореме Муавра – Лапласа, получим
Согласно интегральной теореме Муавра – Лапласа, получим
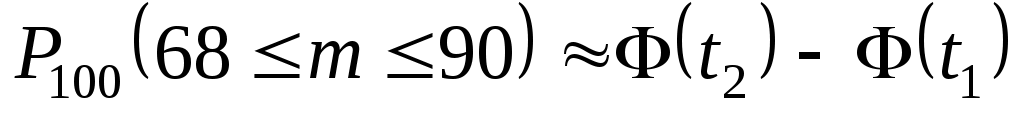 ,
,
где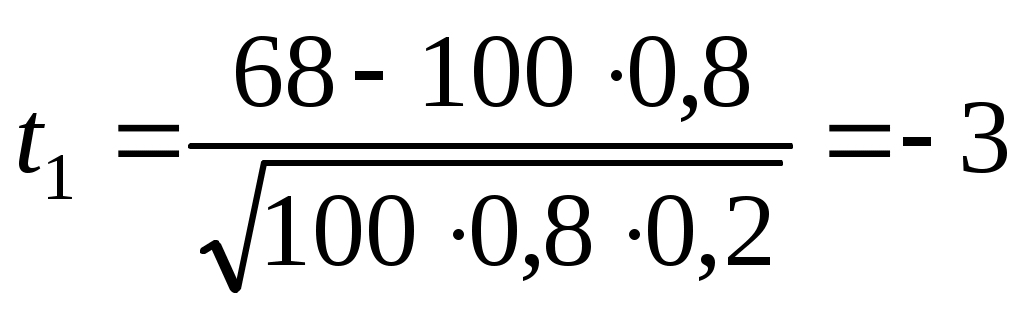 ;
; 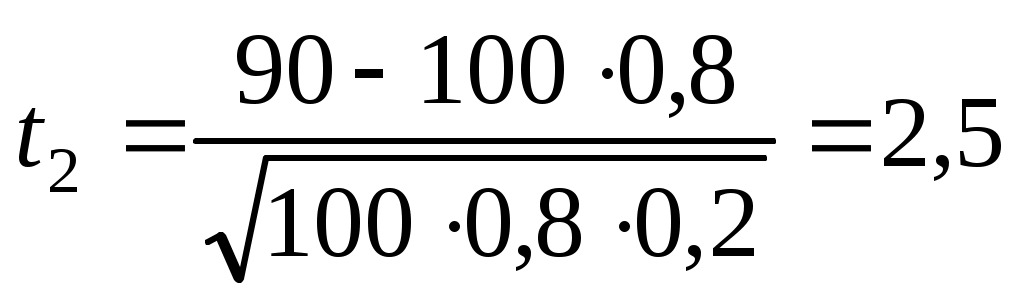 .
.
значения функции Лапласа (прил.2)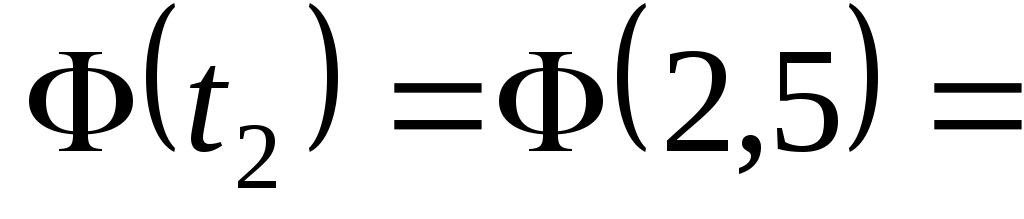 0,4938,
0,4938, 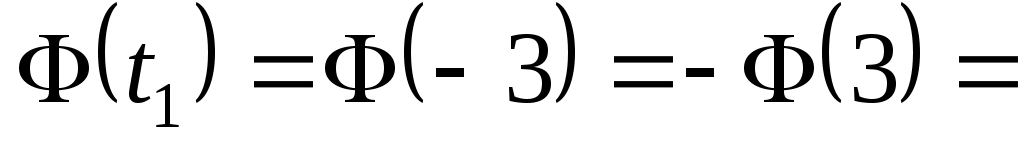 –0,49865. Окончательно получим
–0,49865. Окончательно получим
 = 0,4938 + 0,49865 = 0,99245.
= 0,4938 + 0,49865 = 0,99245.
Предположим, что некоторая величина X может принимать значения x1,x2, …, xn в зависимости от некоторых случайных факторов, так что этим значениям можно сопоставить вероятности p1,p2, …, pn.Такая величина называется случайной величиной (СВ). Свои значения СВ принимает случайным образом.
Рассмотрим два основных типа случайных величин: дискретные и непрерывные.
случайная величина называется дискретной, если она принимает отдельные (изолированные) значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или счетным.
случайная величина называется непрерывной, если она принимает возможные значения, которые сплошь заполняют некоторый интервал.
Значения функции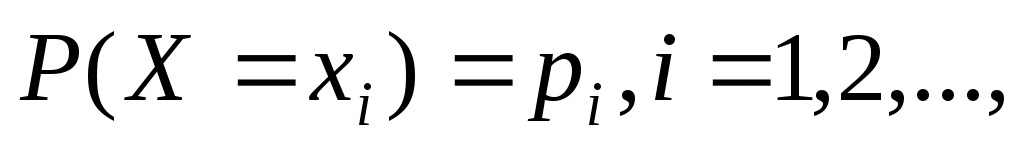 называются рядом распределения вероятностей дискретной случайной величины X.
называются рядом распределения вероятностей дискретной случайной величины X.
Законом распределения дискретной случайной величины называется таблица, в верхней строке которой указаны возможные (различные) значения случайной величины X (в порядке возрастания), а в нижней строке под каждым значением xi – соответствующая вероятность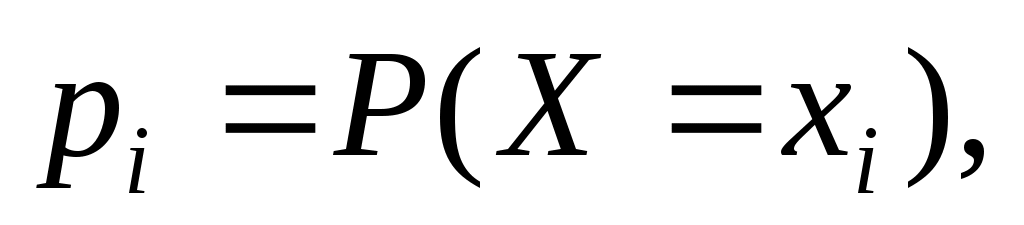 причем
причем 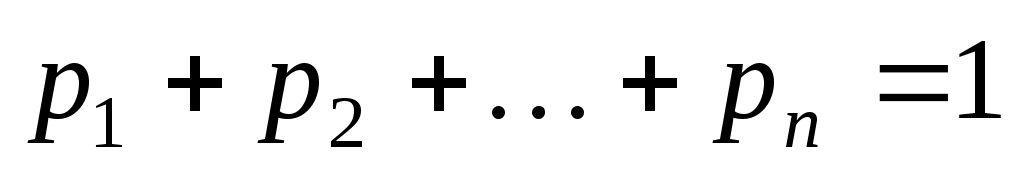 .
.
Графически ряд распределения представляется в виде полигона распределения, причем по оси OX откладывают отдельные значения величины X, а по оси OY – соответствующие им вероятности. Полученные, таким образом точки с координатами (xi,pi), где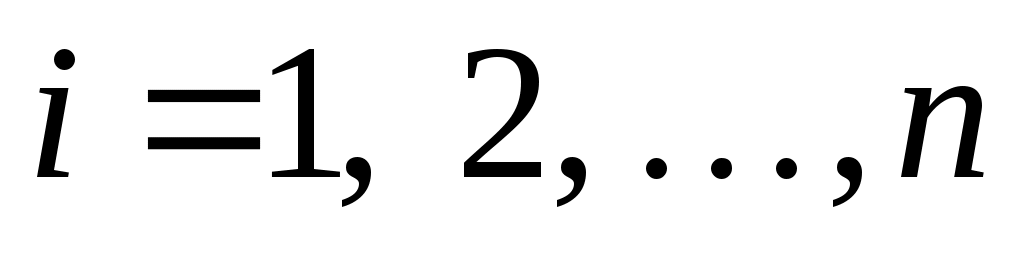
, соединяют прямыми (рис.1).
Интегральной функцией распределения случайной величины X называется функция F(x), выражающая вероятность того, что X примет значение меньшее, чем заданное x:
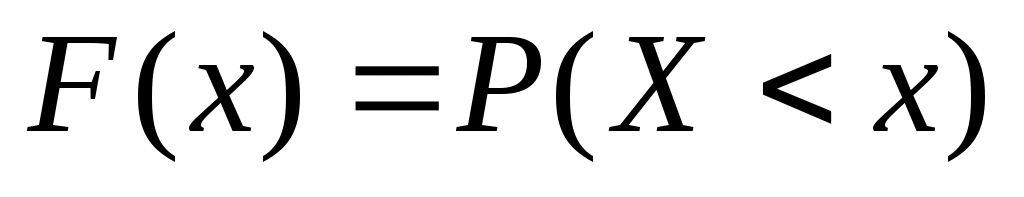 .
.
Следствие: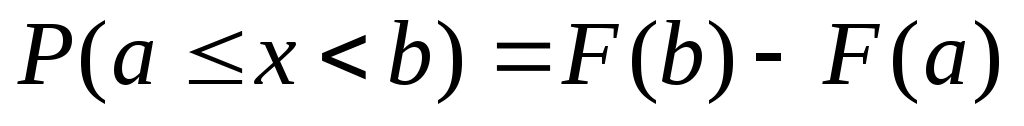 .
.
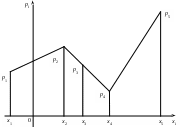
Рис.1. Полигон распределения
Функция F(x) – неубывающая функция (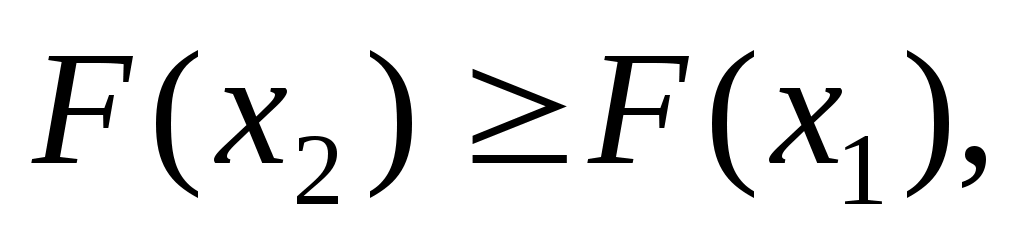 если
если 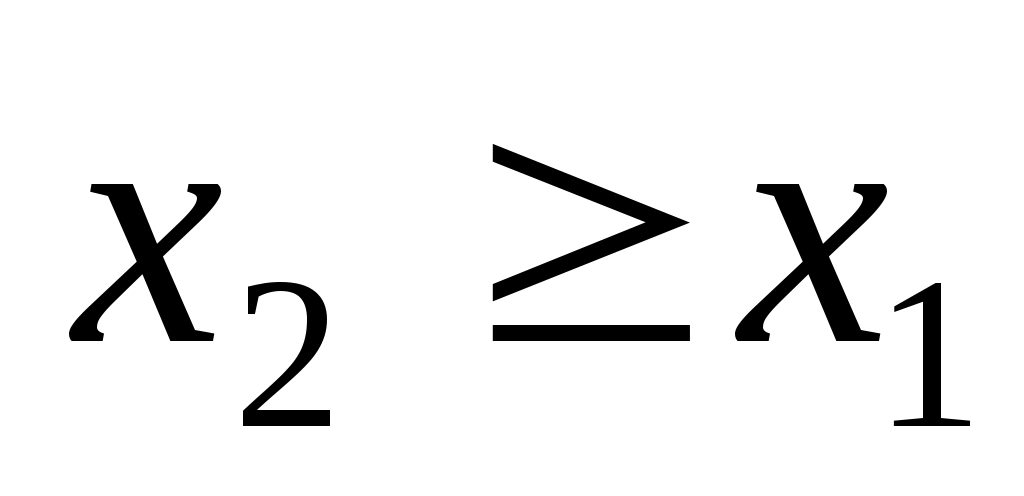 ), кроме того, F(–∞) = 0,F(+∞) = 1. Для непрерывной случайной величины функция распределения непрерывна и существует производная
), кроме того, F(–∞) = 0,F(+∞) = 1. Для непрерывной случайной величины функция распределения непрерывна и существует производная 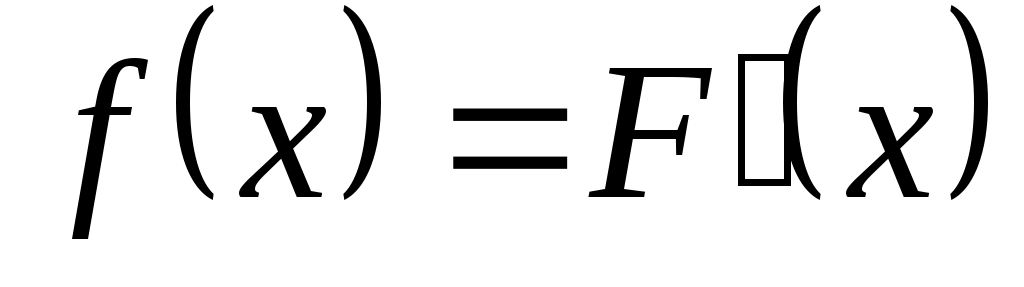 , которая называется плотностью распределения вероятностей или дифференциальной функцией распределения. Плотность любой случайной величины неотрицательна и обладает свойствами:
, которая называется плотностью распределения вероятностей или дифференциальной функцией распределения. Плотность любой случайной величины неотрицательна и обладает свойствами:
1)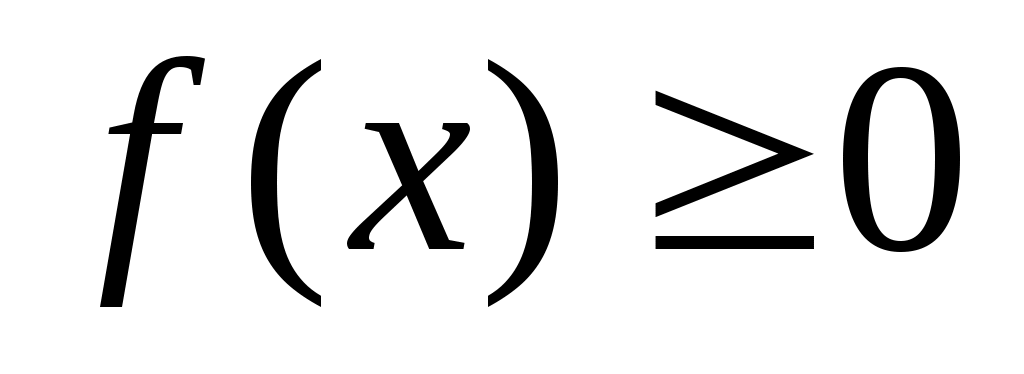 ;
;
2)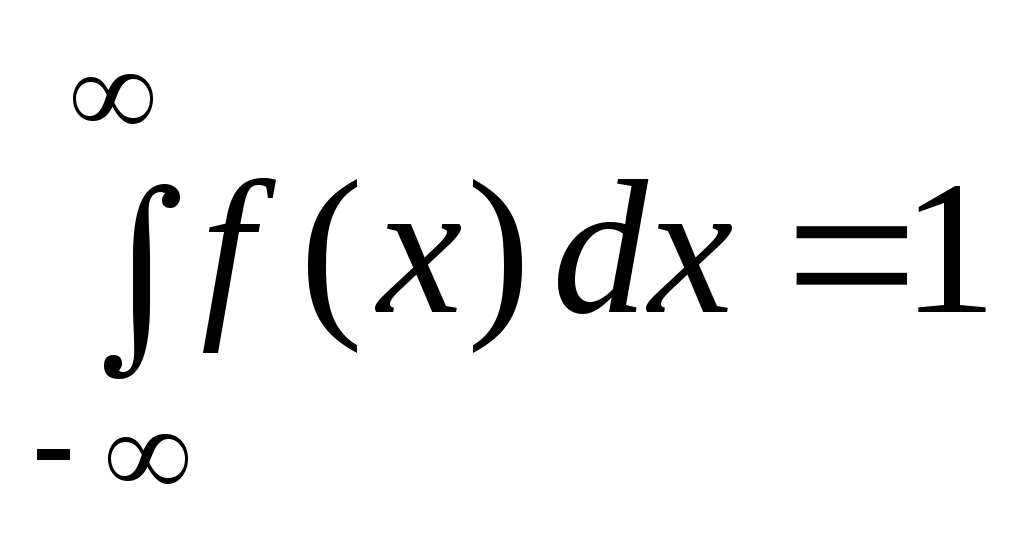 .
.
График дифференциальной функции распределения вероятностей называют кривой распределения. Интегральная функция распределения F(x) выражается через функцию плотности f(x) следующим образом:
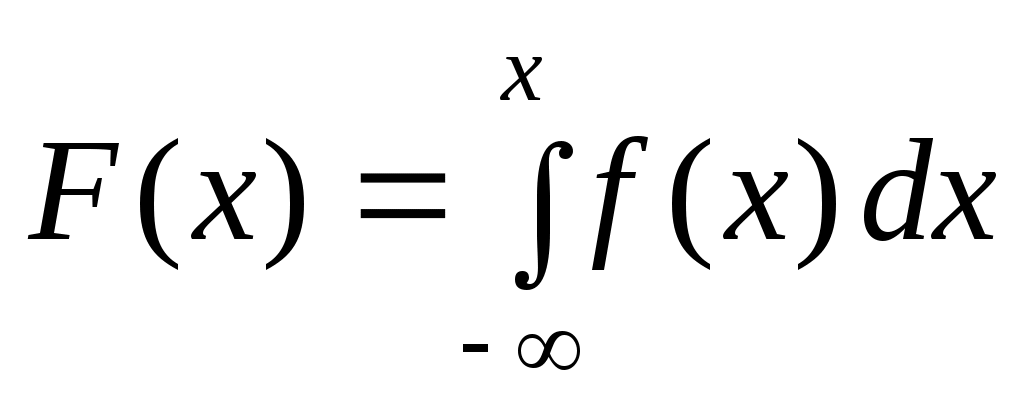 .
.
Для непрерывной случайной величины вероятность принятия некоторого конкретного значения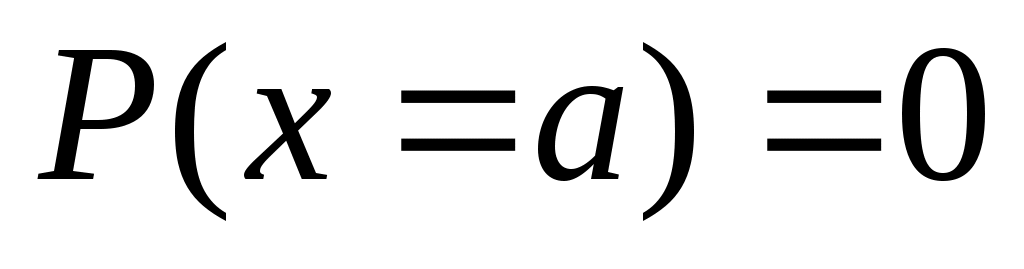 . Тогда
. Тогда
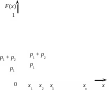
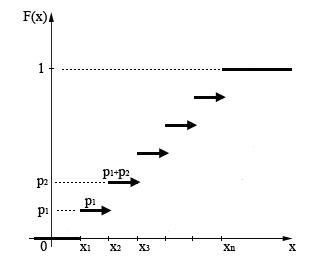
Рис.2. Интегральная функция распределения дискретной случайной величины
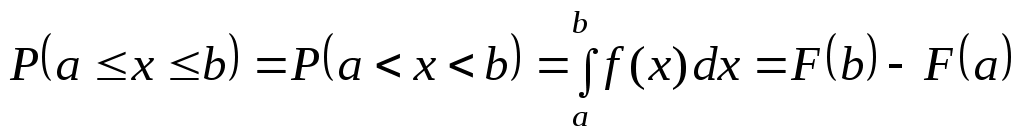 .
.
Если непрерывная случайная величина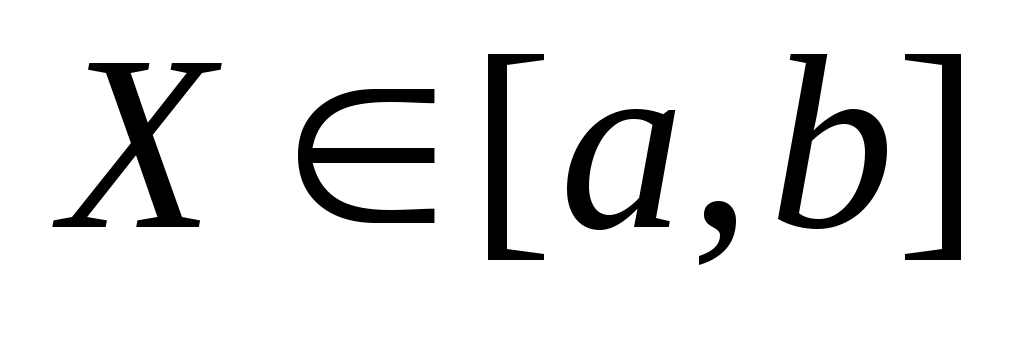 , то
, то 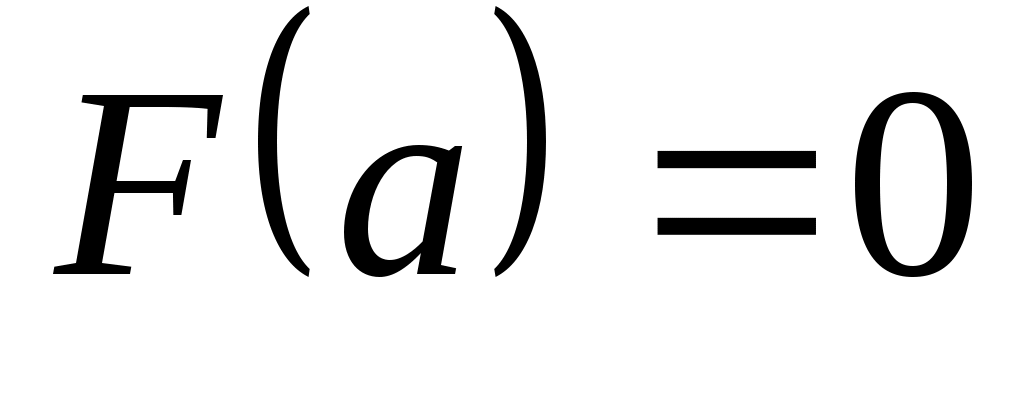 и
и 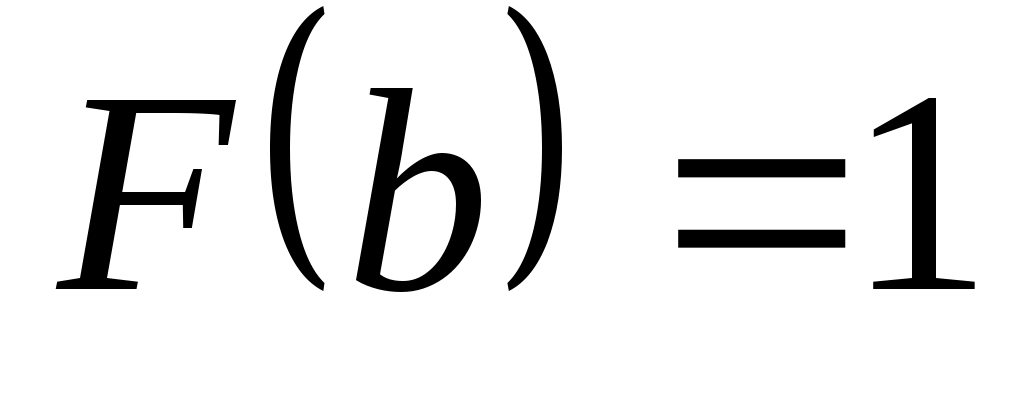 (условия нормировки). Для дискретной случайной величины функция распределения кусочно-постоянна и ступеньки (величины скачков) равны накопленным вероятностям
(условия нормировки). Для дискретной случайной величины функция распределения кусочно-постоянна и ступеньки (величины скачков) равны накопленным вероятностям 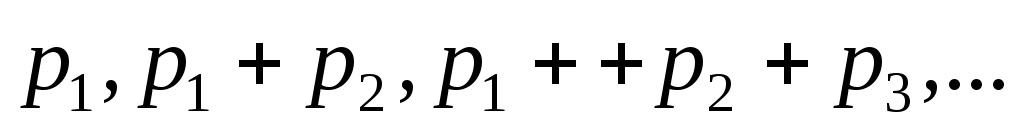 (
(
рис.2).
Пример 10. Непрерывная случайная величина X задана функцией распределения:
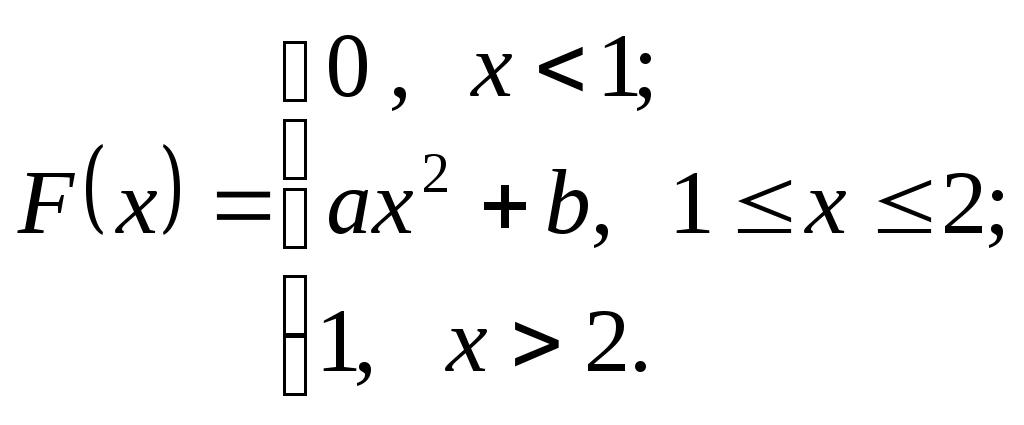
Найти параметры a и b, плотность и вероятность попадания случайной величины в интервал (1, 5; 3).
Решение. По условиям нормировки имеем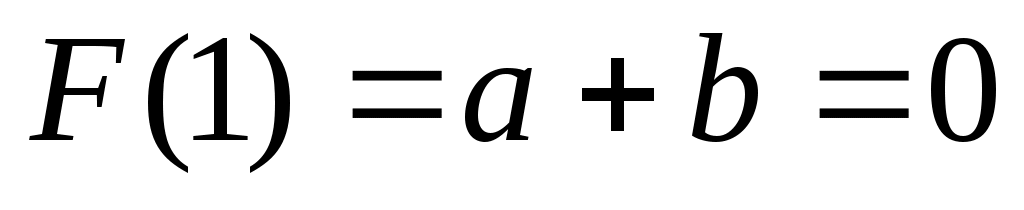 и
и 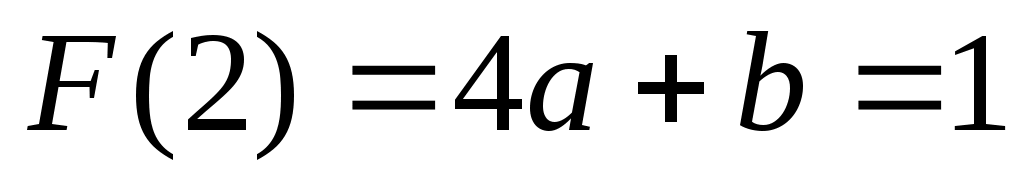 , т.е.
, т.е. 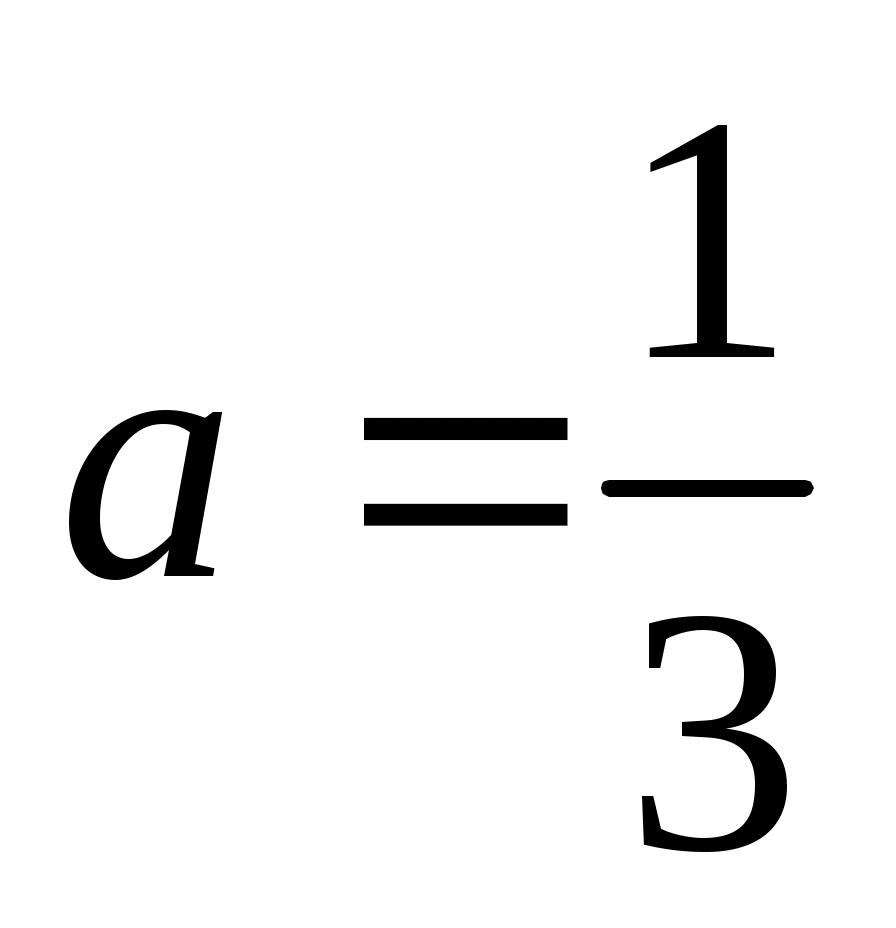 и
и 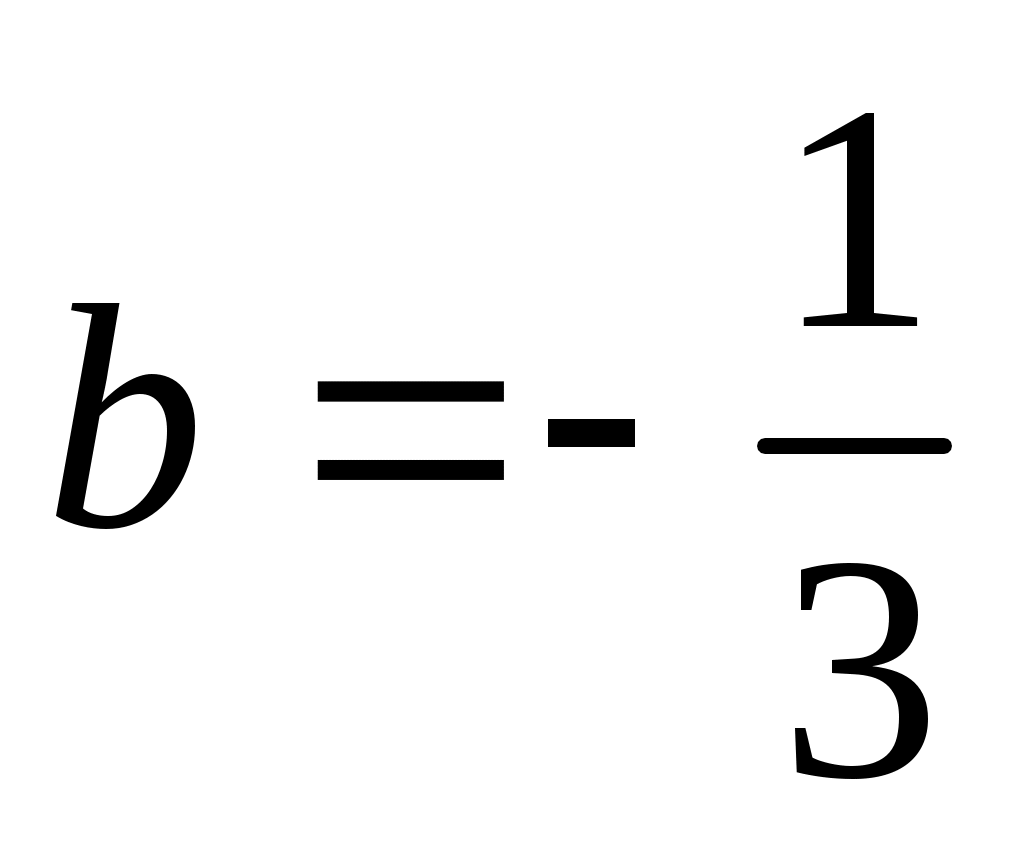 . Тогда функция распределения и ее плотность
. Тогда функция распределения и ее плотность
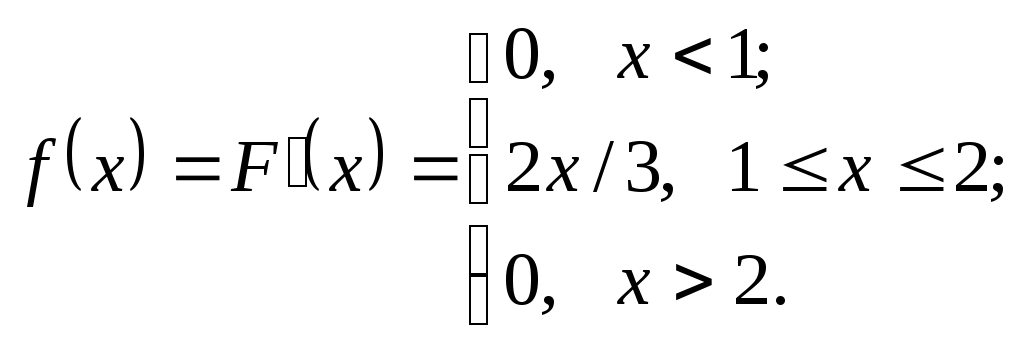
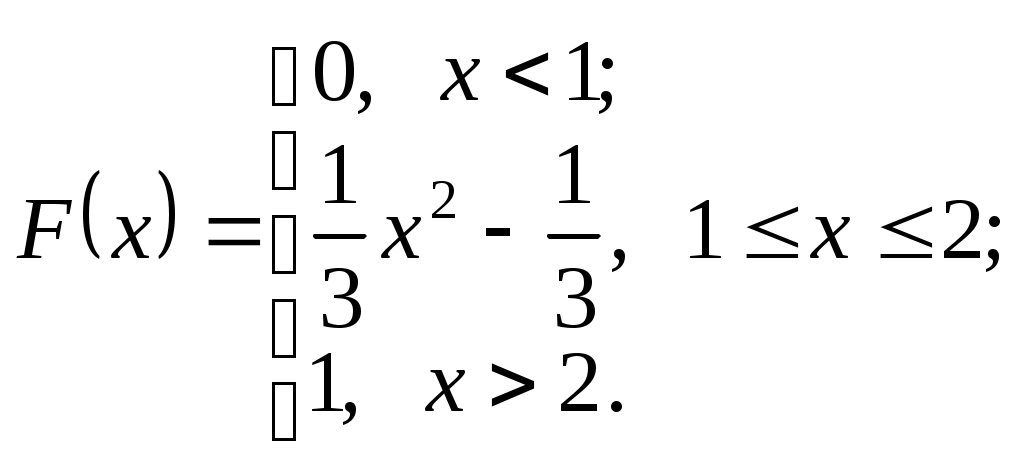
Следовательно, получим
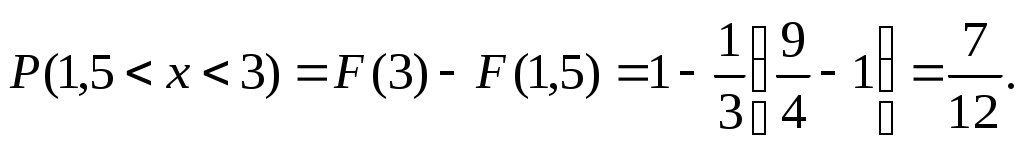
Математическое ожидание или среднее значение случайной величины X есть величина, вычисляемая для дискретной и непрерывной случайных величин по формулам, соответственно:
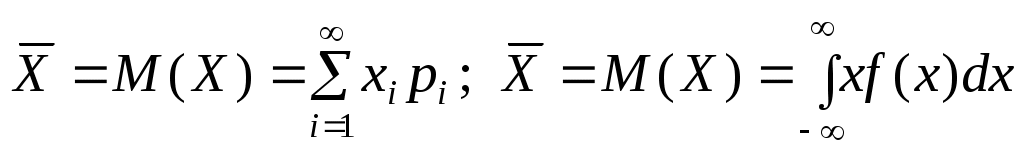 .
.
Дисперсия случайной величины X – это математическое ожидание квадрата ее отклонения от ее математического ожидания:
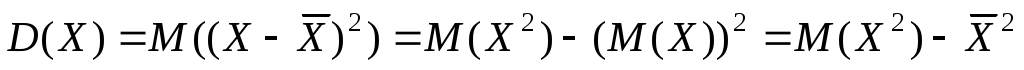 .
.
Дисперсия для дискретной и непрерывной случайной величин, соответственно
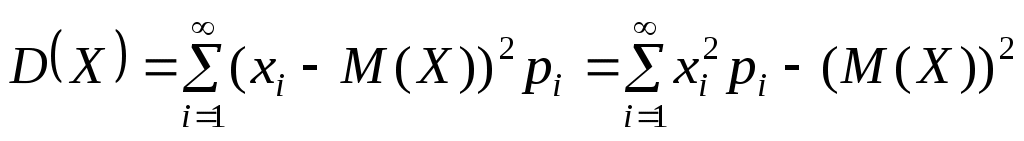 ;
;
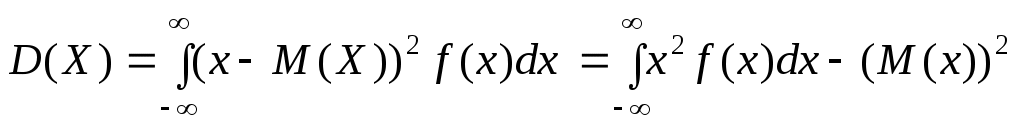 .
.
Среднее квадратичное отклонение случайной величины X обозначим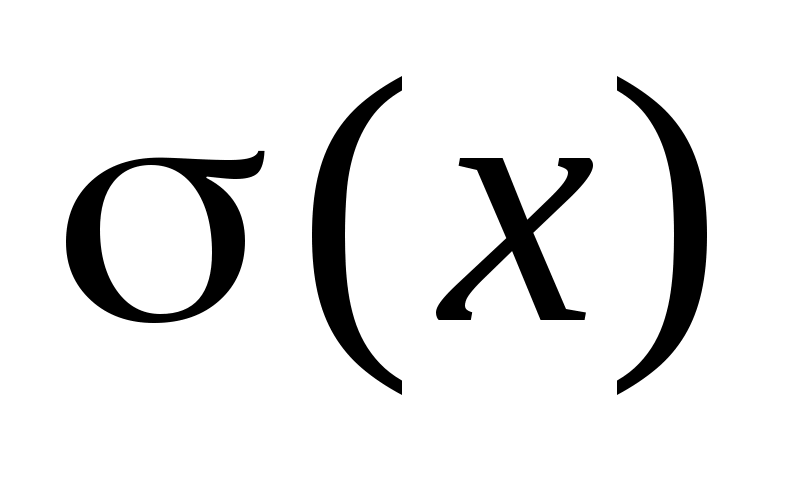 , причем
, причем 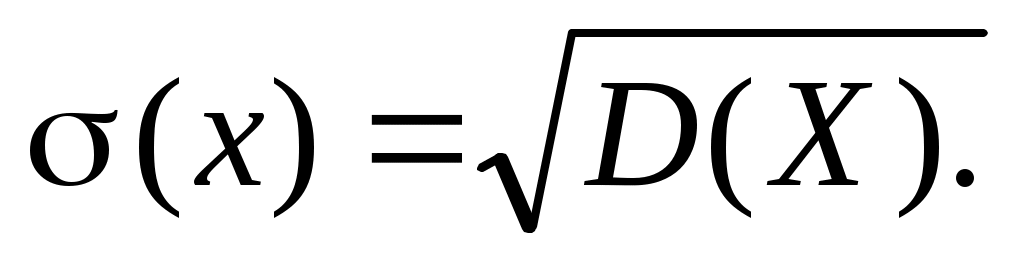
Для функций от случайных величин Y = φ(X) имеем (соответственно для дискретной или непрерывной):
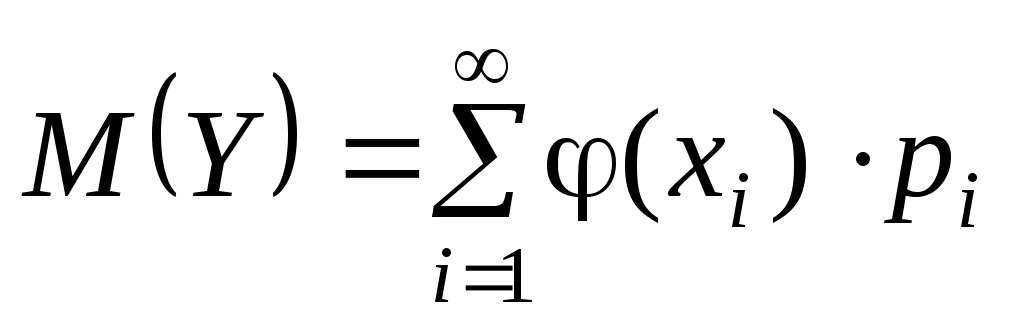 ;
; 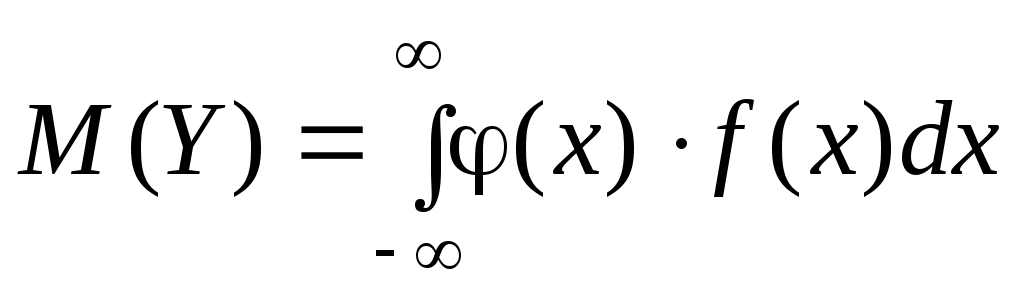 ;
;
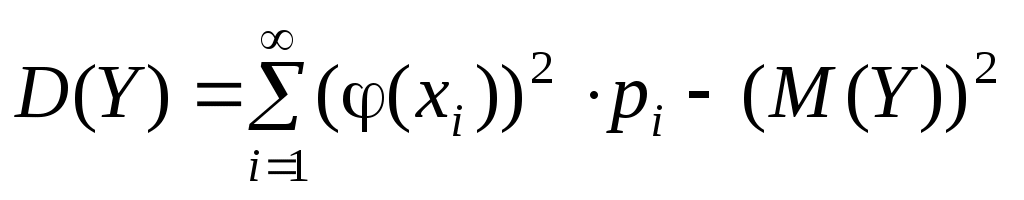 ;
;
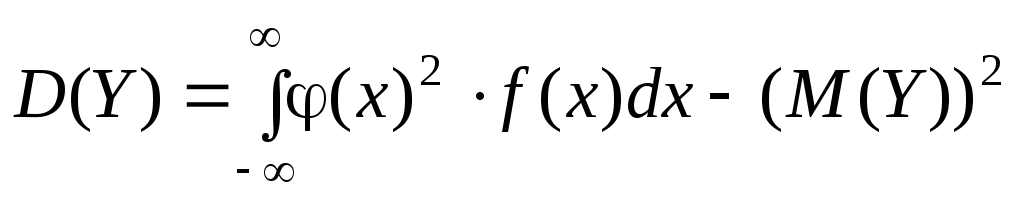
.
Пример 11. Пусть заданное распределение имеет вид
Найти математическое ожидание, дисперсию и среднее квадратичное отклонение.
Решение. Математическое ожидание
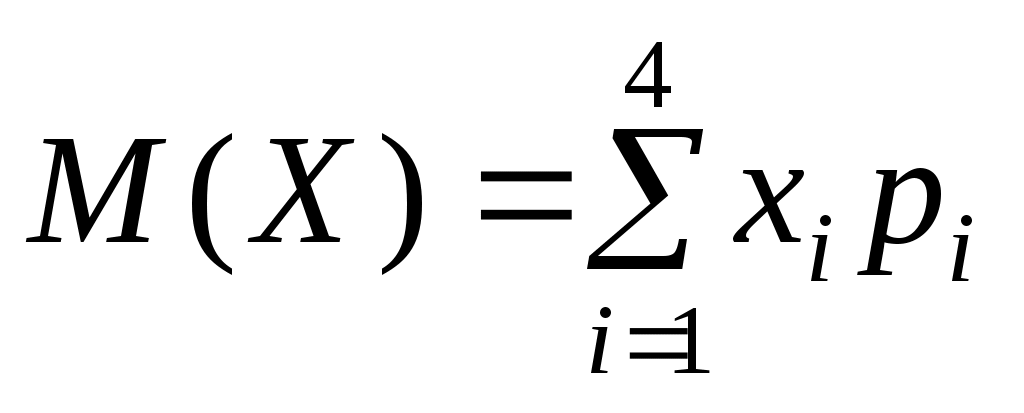 = 1 0,2 + 3 0,3 + 4 0,4 + 6 0,1 =
= 1 0,2 + 3 0,3 + 4 0,4 + 6 0,1 =
= 0,2 + 0,9 + 1,6 + 0,6 = 3,3.
Дисперсия и среднее квадратичное отклонение
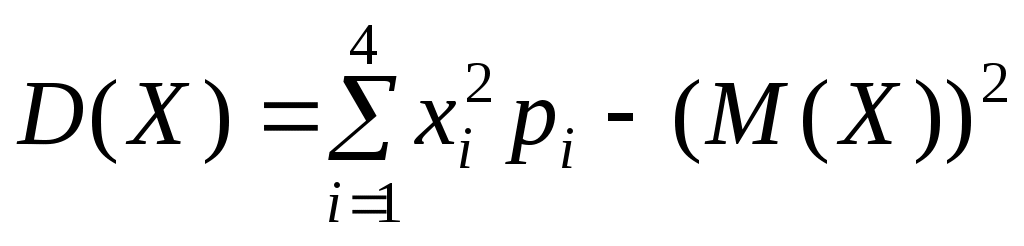 =10,2+90,3+160,4+360,1 –
=10,2+90,3+160,4+360,1 –
– 3,32 = 0,2+2,7+6,4+3,6-3,32 = 2,01;
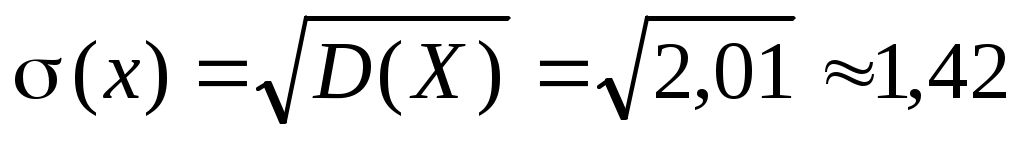 .
.
Пример12.Для случайной величины X из примера 10 найти среднее квадратичное отклонение.
Решение. Математическое ожидание (см. пример 10)
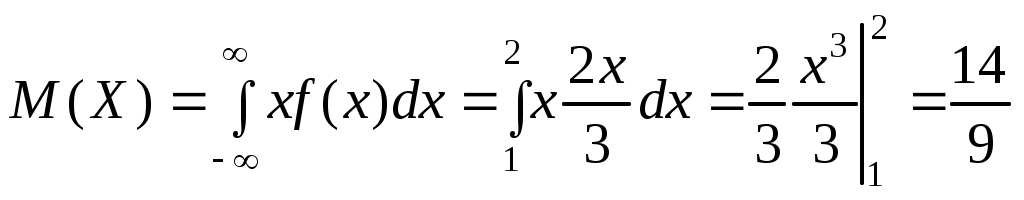 .
.
Дисперсия и среднее квадратичное отклонение
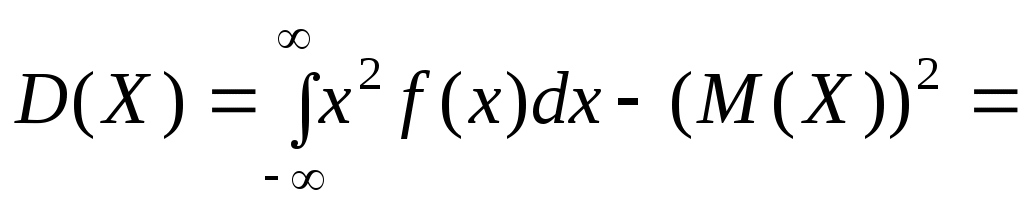
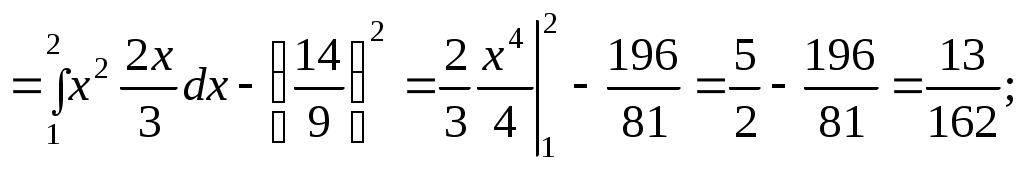
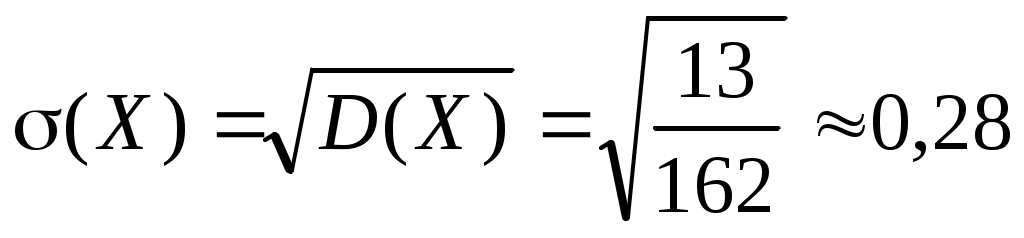 .
.
Дискретная случайная величина X называется распределенной по биномиальному закону, если ее возможные значения равны 0, 1, 2, …, n, а вероятность того, что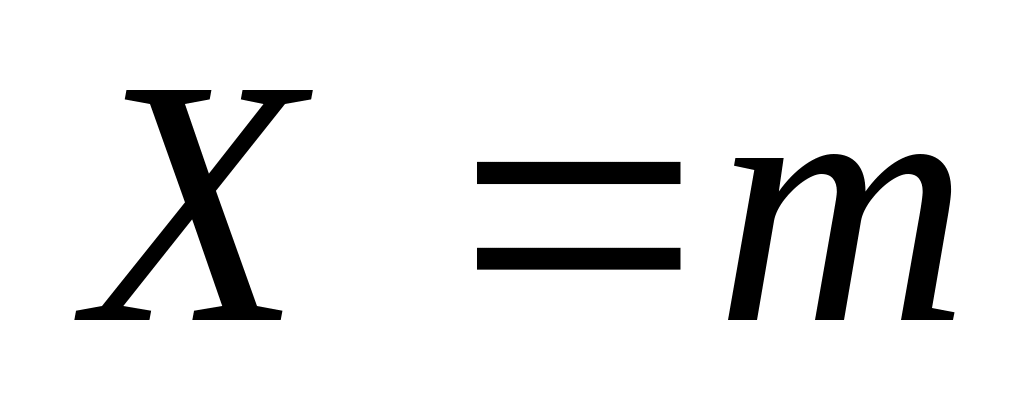 , выражается формулой Бернулли:
, выражается формулой Бернулли:
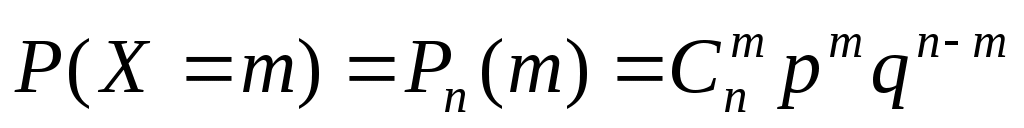 ,
,
где случайная величина X – число появлений некоторого события A в n испытаниях; p – вероятность появления события A в каждом испытании, не изменяющаяся от испытания к испытанию,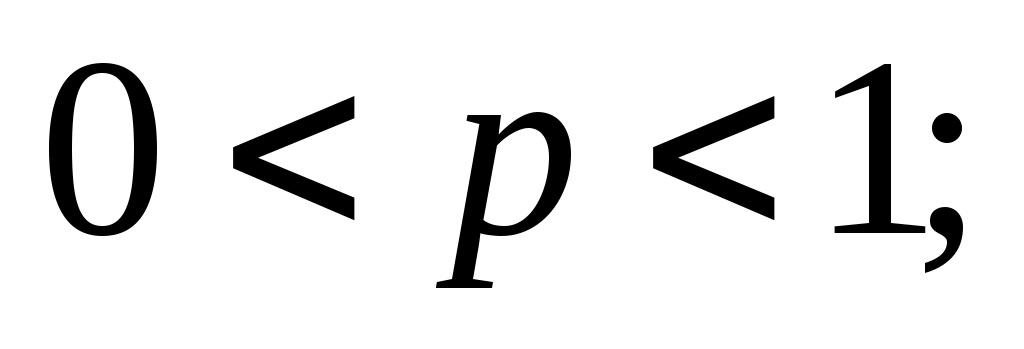 q – вероятность отсутствия события Aв каждом испытании,
q – вероятность отсутствия события Aв каждом испытании, 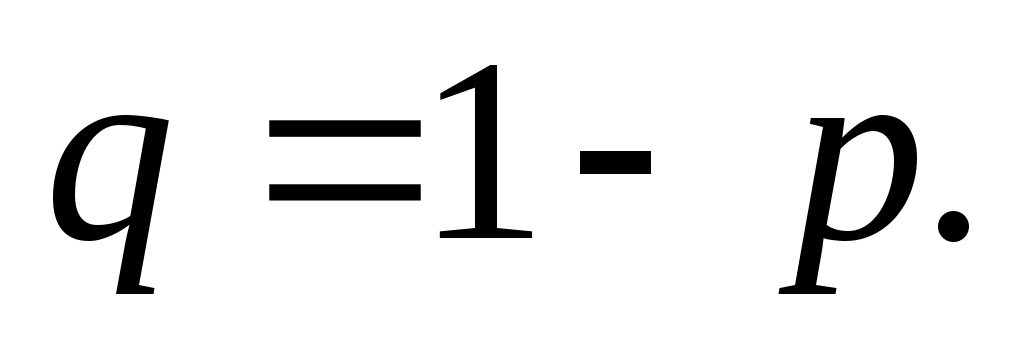
Математическое ожидание и дисперсия случайной величины
При вычислении учтена четность функции Гаусса, а ее значение взято из прил.1.
Пример 9. Вероятность изготовления стандартной детали на автоматическом станке равна 0,8. Найти вероятность того, что среди 100 деталей будет от 68 до 90 стандартных деталей.
Решение. Здесь испытание состоит в проверке, является ли каждая деталь стандартной. Так как вероятность обнаружения стандартной детали в каждом опыте постоянна и равна 0,8, то по условию задачи
где
значения функции Лапласа (прил.2)
1.3. Случайные величины и их числовые характеристики
Предположим, что некоторая величина X может принимать значения x1,x2, …, xn в зависимости от некоторых случайных факторов, так что этим значениям можно сопоставить вероятности p1,p2, …, pn.Такая величина называется случайной величиной (СВ). Свои значения СВ принимает случайным образом.
Рассмотрим два основных типа случайных величин: дискретные и непрерывные.
случайная величина называется дискретной, если она принимает отдельные (изолированные) значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или счетным.
случайная величина называется непрерывной, если она принимает возможные значения, которые сплошь заполняют некоторый интервал.
Значения функции
Законом распределения дискретной случайной величины называется таблица, в верхней строке которой указаны возможные (различные) значения случайной величины X (в порядке возрастания), а в нижней строке под каждым значением xi – соответствующая вероятность
| xi | x1 | x2 | … | xn |
| pi | p1 | p2 | … | pn |
Графически ряд распределения представляется в виде полигона распределения, причем по оси OX откладывают отдельные значения величины X, а по оси OY – соответствующие им вероятности. Полученные, таким образом точки с координатами (xi,pi), где
, соединяют прямыми (рис.1).
Интегральной функцией распределения случайной величины X называется функция F(x), выражающая вероятность того, что X примет значение меньшее, чем заданное x:
Следствие:

Рис.1. Полигон распределения
Функция F(x) – неубывающая функция (
1)
2)
График дифференциальной функции распределения вероятностей называют кривой распределения. Интегральная функция распределения F(x) выражается через функцию плотности f(x) следующим образом:
Для непрерывной случайной величины вероятность принятия некоторого конкретного значения
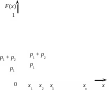

Рис.2. Интегральная функция распределения дискретной случайной величины
Если непрерывная случайная величина
рис.2).
Пример 10. Непрерывная случайная величина X задана функцией распределения:
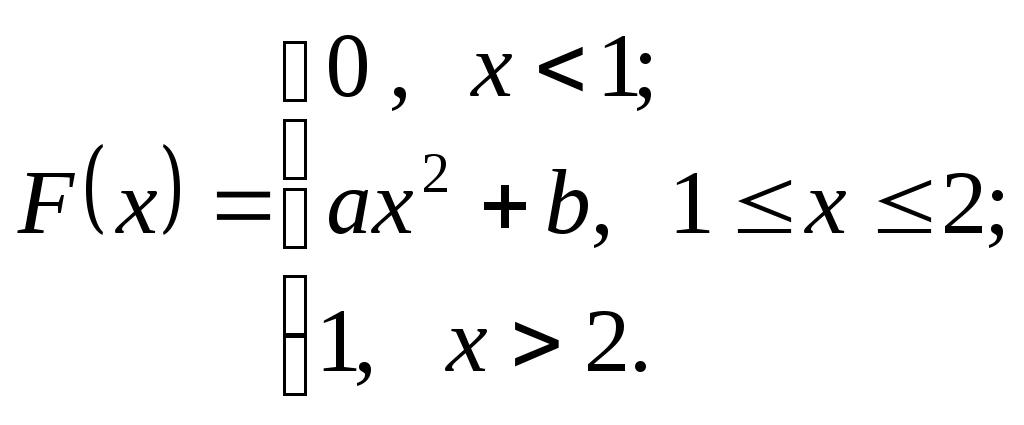
Найти параметры a и b, плотность и вероятность попадания случайной величины в интервал (1, 5; 3).
Решение. По условиям нормировки имеем
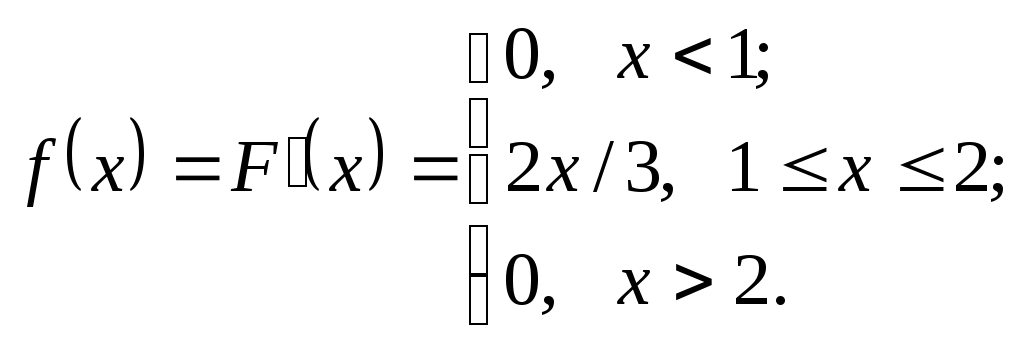
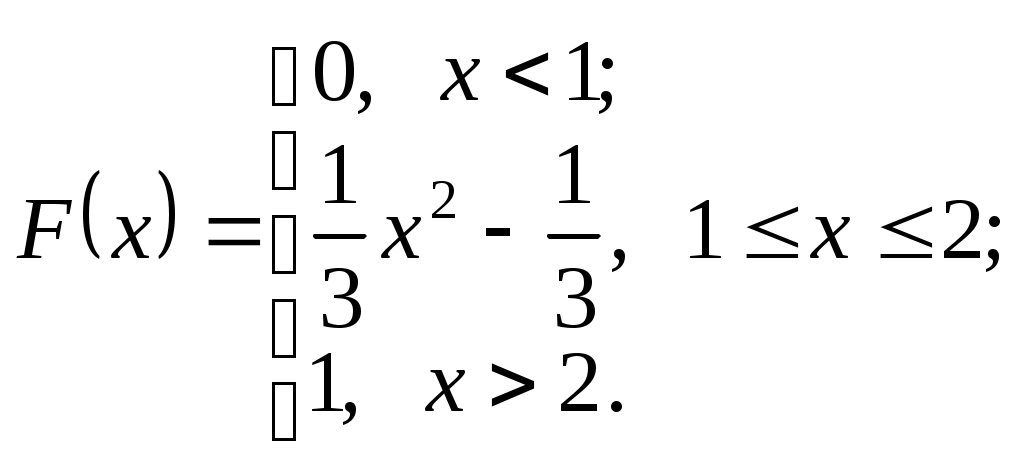
Следовательно, получим
Математическое ожидание или среднее значение случайной величины X есть величина, вычисляемая для дискретной и непрерывной случайных величин по формулам, соответственно:
Дисперсия случайной величины X – это математическое ожидание квадрата ее отклонения от ее математического ожидания:
Дисперсия для дискретной и непрерывной случайной величин, соответственно
Среднее квадратичное отклонение случайной величины X обозначим
Для функций от случайных величин Y = φ(X) имеем (соответственно для дискретной или непрерывной):
.
Пример 11. Пусть заданное распределение имеет вид
| xi | 1 | 3 | 4 | 6 |
| pi | 0,2 | 0,3 | 0,4 | 0,1 |
Найти математическое ожидание, дисперсию и среднее квадратичное отклонение.
Решение. Математическое ожидание
= 0,2 + 0,9 + 1,6 + 0,6 = 3,3.
Дисперсия и среднее квадратичное отклонение
– 3,32 = 0,2+2,7+6,4+3,6-3,32 = 2,01;
Пример12.Для случайной величины X из примера 10 найти среднее квадратичное отклонение.
Решение. Математическое ожидание (см. пример 10)
Дисперсия и среднее квадратичное отклонение
Дискретная случайная величина X называется распределенной по биномиальному закону, если ее возможные значения равны 0, 1, 2, …, n, а вероятность того, что
где случайная величина X – число появлений некоторого события A в n испытаниях; p – вероятность появления события A в каждом испытании, не изменяющаяся от испытания к испытанию,
Математическое ожидание и дисперсия случайной величины