ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 171
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2.ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Пусть для изучаемой случайной величины X получен ряд ее значений x1, x2, …, xn, который называют выборкой объема n из множества всех возможных значений X (генеральной совокупности). Эти значения xi являются случайными величинами, так как меняются от выборки к выборке.
Важно, чтобы опыты для получения достоверных и правильно представляющих (репрезентативных) генеральную совокупность результатов проводились в одинаковых условиях и независимо друг от друга. Значит, случайные величины xi будут независимы и одинаково распределены. Согласно центральной предельной теореме (ЦПТ) распределение среднего значения
Если число n невелико (

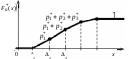
Рис.3. Гистограмма
Рис.4. Эмпирическая функция
распределения
По теореме Бернулли (т.е. по следствию закона больших чисел) эмпирическая вероятность приближается к теоретической вероятности при
Пример 14. Выборка задана вариационным рядом:
| | 0 | 3 | 5 | 9 | 11 | 13 | 17 | 19 | 20 | 24 | 26 | 28 | 31 | 34 | 39 | 40 | 42 |
| | 4 | 2 | 5 | 3 | 6 | 3 | 3 | 4 | 3 | 2 | 1 | 3 | 3 | 2 | 1 | 3 | 2 |
(k = 1,2,…,17).
Произвести группировку значений и по сгруппированному вариационному ряду построить эмпирическую функцию распределения и гистограмму плотности.
Решение. Вводим интервалы группировки:
(чтобы первое значение
Для сгруппированного вариационного ряда значения равны серединам интервалов:
Объем выборки
Эмпирические вероятности равны:
Отметим, что
Накопленные вероятности:
за
за
за