Файл: Лабораторная работа Описательная статистика Основная литература.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 219
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа № 1. Описательная статистика
Основная литература.
Статистические методы в педагогике и психологии: учебно-методическое пособие для бакалавров, магистрантов, аспирантов, соискателей. Изд. 2-е доп. / А.А. Русаков, Ю.И. Богатырева. – Тула: Изд-во Тул. гос. пед. ун-та, 2012. - 137 с.
Описательная (дескриптивная) статистика – это раздел математической статистики, предназначенный для представления данных в наглядном виде и описания информации в терминах математической статистики и теории вероятностей.
Основной величиной в статистических измерениях является единица статистической совокупности (например, любой из критериев оценки уровня сформированности педагогической культуры). Единица статистической совокупности характеризуется набором признаков, переменных или параметров. Значения каждого параметра могут быть различными и в целом образовывать ряд случайных значений x1, х2, …, хn.
Переменная (variable) — это параметр измерения, который можно контролировать или которым можно манипулировать в исследовании. Так как значения переменных не постоянны, нужно научиться описывать их изменчивость. Для этого разработаны описательные статистики: минимум, максимум, размах, среднее, дисперсия, стандартное отклонение, медиана, квартили, мода.
Относительное значение параметра — это отношение числа объектов, имеющих исследуемый параметр, к величине выборки. Выражается относительным числом или в процентах (например, процентное значение числа правонарушителей среди учащихся 10-11 классов, процент неуспевающих учеников класса).
Удельное значение параметра – это расчетная величина, показывающая количество объектов с данным параметров, которое содержалось бы в условной выборке, состоящей из 10, или 100, 1000 и т. д. объектов (например, количество правонарушений на 1000 человек).
Минимум (xmin) и максимум (xmax) – это минимальное и максимальное значения параметра соответственно.
Размах (разброс, R) — это разница между минимальным и максимальным значением параметра R= xmax- xmin.
Среднее значение (оценка среднего, выборочное среднее, Mx,
)– сумма значений параметра, деленная на количество элементов выборки (n). Формула для выборочного среднего имеет вид:
х =
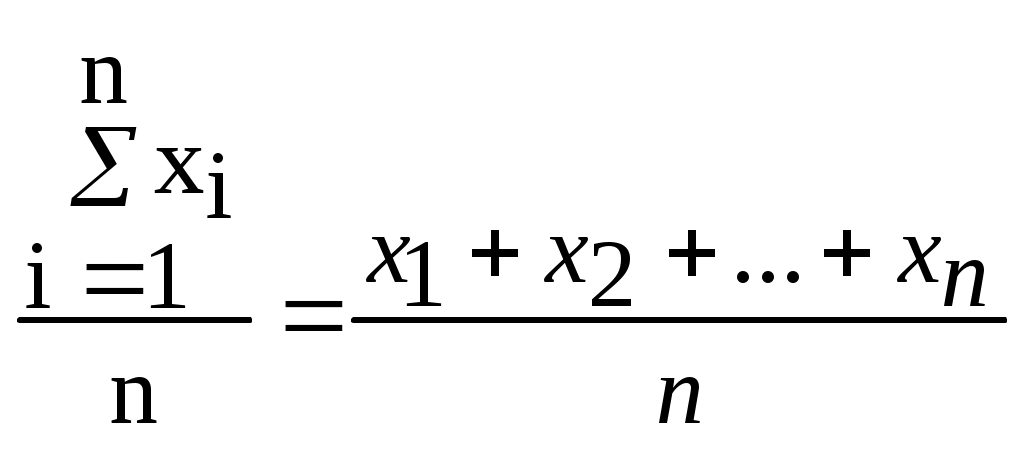 (1)
(1)Пример 1: наблюдение посещаемости четырех внеклассных мероприятий в экспериментальном (20 учащихся) и контрольном (30 учащихся) классах дали значения (соответственно): 18, 20, 20, 18 и 15, 23, 10, 28. Среднее значение посещаемости в обоих классах получается одинаковое - 19. Однако видно, что в контрольном классе этот показатель подчинен воздействию каких-то специфических факторов.
Выборочное среднее является той точкой, сумма отклонений наблюдений от которой равна нулю. Формально это записывается следующим образом: (х - х1) + (х - х2) + ... + (х - хn) =0. Преимущества среднего значения в том, что оно может аккумулировать или уравновешивать все индивидуальные отклонения параметра.
Для оценки степени разброса (отклонения) какого-то показателя от его среднего значения, наряду с максимальным и минимальным значениями, используются понятия дисперсии и стандартного отклонения.
Дисперсия выборки (выборочная дисперсия, D, 2) – это мера изменчивостипараметра выборки (мера рассеивания случайной величины). Термин впервые введен Фишером в 1918 году. Дисперсия – это среднее арифметическое квадратов отклонений значений параметра от его среднего значения. Выборочная дисперсия вычисляется по формуле:
2 =
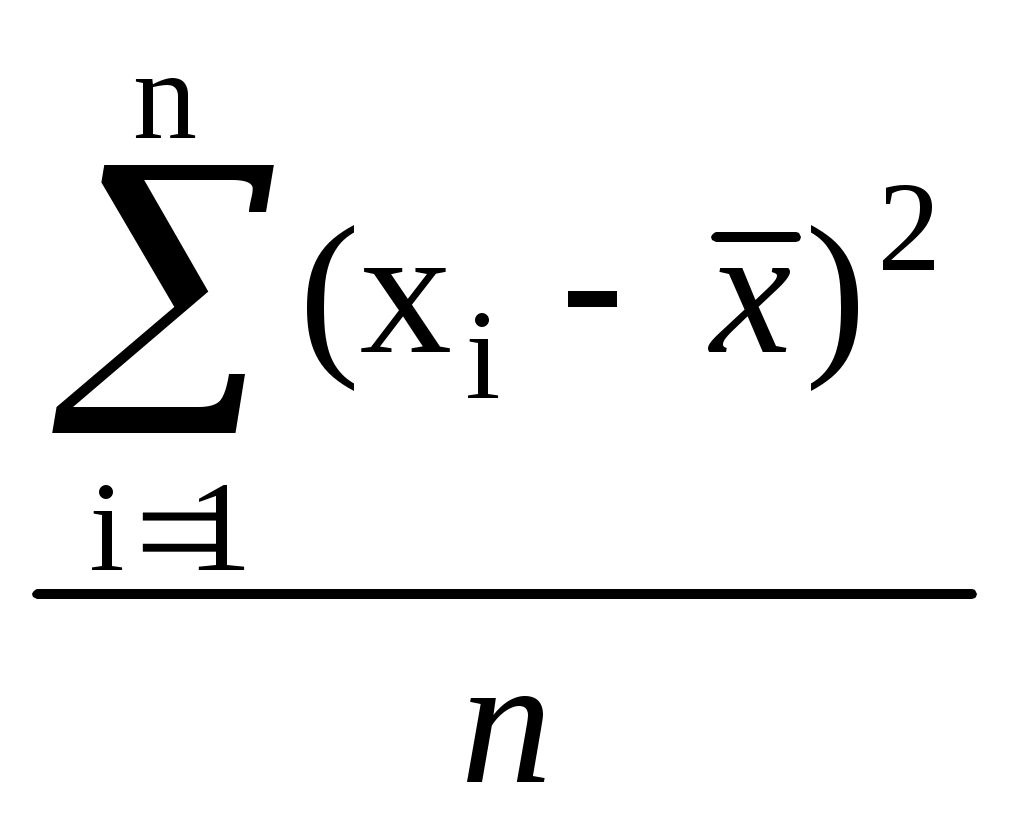 (2)
(2)где х — выборочное среднее,
n — число наблюдений (объем выборки).
Дисперсия численно меняется от нуля до бесконечности. Крайнее значение 0 означает отсутствие изменчивости (значения параметра постоянны).
Стандартное отклонение (среднее квадратическое отклонение, , s)вычисляется как корень квадратный из дисперсии. Чем выше дисперсия или стандартное отклонение, тем сильнее разбросаны значения переменной относительно среднего.
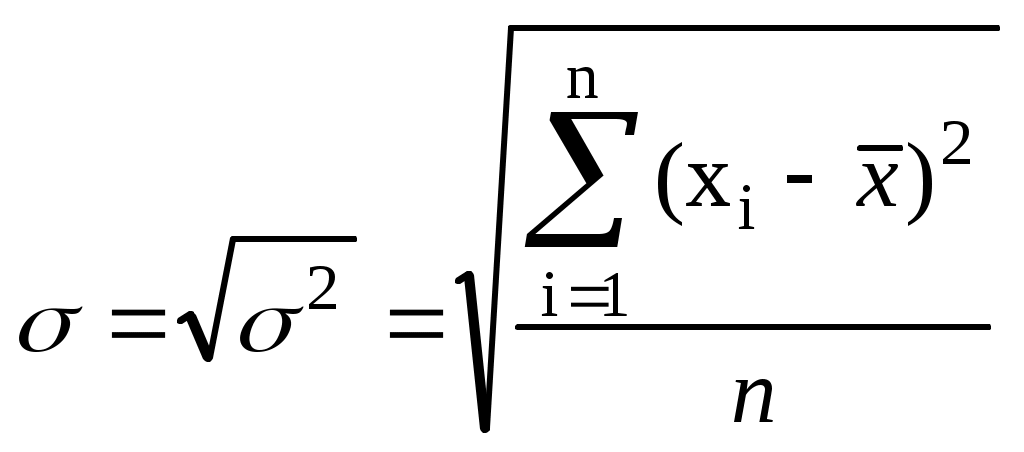 (3)
(3)Коэффициент вариации () – отношение стандартного отклонения к выборочному среднему, выраженное в процентах:
(4)
Пример 2: Для предыдущего примера 1 получаем значения среднего, дисперсии, коэффициента вариации и стандартного отклонения:
| Значения описательной статистики | | 2 | | |
| Экспериментальный класс | 19 | 1 | 1 | 6% |
| Контрольный класс | 19 | 48,5 | 6,96 | 37% |
Это означает, что в одном классе (экспериментальном) посещаемость высокая, стабильная, а в другом (контрольный класс) - отличается непостоянством.
Медиана (Md, Me, mе,
Рассмотрим способыопределения медианы при различных значениях n. Для нахождения медианы необходимо прежде всего упорядочить (ранжировать) выборку по возрастанию (или убыванию) значений, то есть все измерения записывают в ряд по возрастанию значений. Если число измерений n нечетное, то медиана численно равна значению выборки, стоящему точно в середине, или на
Например, медиана (
Если число измерений четное, то медиана численно равна среднему арифметическому значений ряда
, стоящих в середине, или на
Например, медиана (
Квартили (
Различают верхнюю квартиль, которая больше медианы и делит пополам верхнюю часть выборки (значения параметра больше медианы), и нижнюю квартиль, которая меньше медианы и делит пополам нижнюю часть выборки.
Нижнюю квартиль часто обозначают символом 25%, это означает, что 25% значений параметра меньше нижней квартили. Верхнюю квартиль часто обозначают символом 75%, это означает, что 75% значений параметра меньше верхней квартили.
Таким образом, три точки — нижняя квартиль, медиана и верхняя квартиль - делят выборку на 4 равные части. ¼ наблюдений лежит между минимальным значением и нижней квартилью, ¼ - между нижней квартилью и медианой, ¼ - между медианой и верхней квартилью, ¼ - между верхней квартилью и максимальным значением выборки.
Мода (Mo,
Сложность в том, что редкая выборка имеет единственную моду. Правила нахождения моды:
-
если выборка имеет несколько мод, то говорят, что она мультимодальна или многомодальна (имеет два или более «пика»). Выборка: 2, 6, 6, 8, 9, 9, 10 – Mo = 6, 9. -
Выборка может и не иметь моды, тогда говорят, что данное распределение не имеет моды. Выборка: 2, 6, 7, 8, 9, 12, 10 – нет Mo. -
Если в выборке одинаково часто встречаются значения параметра, стоящие друг за другом, то мода будет численно равна среднему арифметическому данных этих двух значений. Выборка: 2, 5, 5, 6, 6, 8, 10 – Mo = 5,5.
Асимметрия (As) – это свойство распределения выборки, которое характеризует несимметричность распределения показателя. На практике симметричные распределения встречаются редко и чтобы выявить и оценить степень асимметрии, вводят следующую меру:
Асимметрия бывает положительной и отрицательной.
Эксцесс (Ех) – это мера плосковершинности или остроконечности графика распределения измеренного признака (мера крутости кривой распределения).
Эксцесс можно вычислить по формуле:
Практическая работа 1. Использование электронных таблиц MS Excel для вычисления показателей описательной статистики
Пакет MS Excel оснащен средствами статистической обработки данных. И хотя Excel существенно уступает специализированным статистическим пакетам обработки данных, тем не менее, этот раздел математики представлен в MS Excel наиболее полно. В него включены основные, наиболее часто используемые статистические процедуры: средства описательной статистики, проверка на нормальность, критерии различия, корреляционные и другие методы, позволяющие проводить необходимый статистический анализ экономических, психологических, педагогических и медико-биологических типов данных.
Вся помещаемая в электронную таблицу информация хранится в отдельных клетках (ячейках) рабочей таблицы. Но ввести информацию можно только в текущую клетку (активную ячейку). Таблица состоит из листов. С помощью адреса в строке формул и табличного курсора Excel указывает, какая из клеток рабочей таблицы является текущей. В основе системы адресации клеток рабочей таблицы лежит комбинация буквы (или букв) столбца и номера строки, например A2, B12.
Рассмотрим, как можно использовать электронные таблицы MS Excel для расчета показателей описательной статистики.
1.1. Использование специальных функций
В мастере функций MS Excel имеется ряд специальных функций для вычисления выборочных характеристик:
| № п/п | Название функции | Назначение функции |
| | СРЗНАЧ | вычисляет среднее арифметическое из нескольких массивов (аргументов) чисел. Аргументы число1, число2, ... — это от 1 до 30 параметров выборки, для которых вычисляется среднее |
| | МИН | возвращает минимальное значение выборки |
| | МАКС | возвращает максимальное значение выборки |
| | МЕДИАНА | позволяет получать медиану заданной выборки |
| | МОДА | вычисляет наиболее часто встречающееся значение в выборке |
| | ДИСП | позволяет рассчитать дисперсию по исходным параметрам выборки |
| | СТАНДОТКЛОН | вычисляет стандартное отклонение |
| | КВАРТИЛЬ | вычисляет квартили распределения. Функция имеет формат КВАРТИЛЬ (массив, часть), где массив – интервал ячеек, содержащих значения СВ; часть определяет какая квартиль должна быть найдена (0 – минимальное значение, 1 – нижняя квартиль, 2 – медиана, 3 – верхняя квартиль, 4 – максимальное значение распределения). |
| | ЭКСЦЕСС | вычисляет оценку эксцесса по выборочным данным |
| | СКОС | позволяет оценить асимметрию выборочного распределения |