Файл: севастопольский государственный универитет морской институт.docx

11.4 Расчет эквивалентного бруса

Под эквивалентным брусом понимают совокупность всех продольных связей корпуса судна, принимающих участие в восприятии общего изгиба, которые рассматриваются как одна балка. Для проверки прочности необходимо найти момент инерции, моменты сопротивления и статические моменты миделевого поперечного сечения корпуса судна, рассматривая его в целом как балку.

При расчете момента сопротивления сечения корпуса учитываются все непрерывные продольные связи, включая непрерывные продольные комингсы и участки палуб между ними (если конструк­ция предусматривает два и более рядов люков), если они эффективно поддерживаются продольными переборками, в том числе переборками подпалубных цистерн (вторыми бортами).

При использовании стали повышенной прочности и продольные непрерывные связи, выполненные из этой стали, должны прости­раться в нос и в корму за пределы средней части судна настоль­ко, чтобы момент сопротивления сечения корпуса в месте измене­ния предела текучести стали имел величину и менее требуемой для такого же корпуса, выполненного из обычной стали.

Элементы эквивалентного бруса вычисляются в таблице 11.4. Схема эквивалентного бруса представлена на рисунке 11.4,а ось сравнения принимаем нижнюю кромку днищевой обшивки.

Таблица 11.4 – Расчет элементов эквивалентного бруса





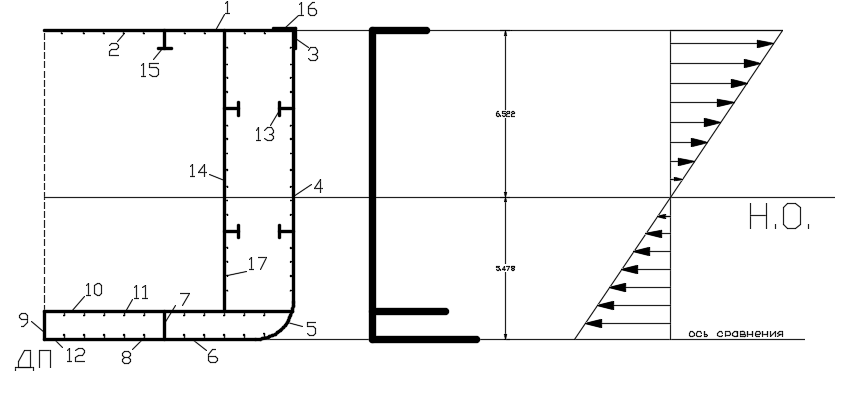
Рисунок 11.4 – Схема эквивалентного бруса

Собственные моменты инерции следует учитывать только для связей, ориентированных вертикально и имеющих сравнительно большую высоту листов.

После заполнения столбцов с 1-го по 7-й таблицы 11.4, вычисляются следующие элементы эквивалентного бруса:

• 
  отстояние нейтральной оси от оси сравнения по формуле:
  

е_но=В/А=43737,06/7984=5,478м

• 
  момент инерции относительно нейтральной оси по формуле:
  

I_но= 2(C-(В²/А))= 2∙(390868,686–(43737,06²/7984)) = 302517,468 см²∙м²

где А – сумма площадей продольных связей;

В – сумма статических моментов площадей продольных связей относительно оси сравнения;

С – моменты инерции, полученные относительно оси сравнения (сумма столбцов 7 и 8).

---

• 
  моменты сопротивления поперечного сечения относительно крайней точки палубы и днища по формуле:
  

W_п =I_но/z_п =302517,468/6,522= 46387,134 см²∙м

W_д =I_но/z_д = 302517,468/5,478= 55219,852 см²∙м

где z_п – отстояние нейтральной оси до крайней связи палубы, м

z_д – отстояние нейтральной оси до крайней связи днища, м

Вычисление нормальных напряжений в первом приближении

При общем изгибе в поперечных сечениях корпуса возникают нормальные напряжения, уравновешивающие внешний изгибающий мо­мент. Нормальные напряжения в продольных связях вычисляются по формулам:

• 
  на вершине волны
  

σ = k_вв·z; МПа (11.2)

• 
  на подошве волны
  

σ = k_пв·z; МПа, (11.3)

где k_вв, k_пв – коэффициенты, соответственно равные

k_вв =М_ВВмах /i_но = 756169/302517,468= 2,5 [ ];

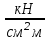k_пв = М_ПВ.мах /i_но = 235968/302517,468= 0,78 [ ]

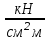где М_вв, М_пв – расчетные изгибающие моменты для положения судна на вершине и подошве волны соответственно, кНм;

I_н.о –момент инерции сечения относительно нейтральной оси, см²∙м²;

z – отстояние рассматриваемой связи от нейтральной оси, положительное при отсчете вниз, м.

Изгибающий момент считается положительным при перегибе судна. Вычисленные таким образом нормальные напряжения для различных расчетных положений корпуса представлены в таблице 11.4.

10.4 Определение касательных напряжений

Величина касательных напряжений, определяемая по формуле:

,

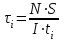где N – перерезывающая сила в данном сечении (N_max = 17534кН);

S – статический момент;

t_i – толщина i-ой связи;

I – момент инерции сечения относительно нейтральной оси

(I_но = 302517,468∙м²).

Момент инерции и статический момент, входящие в формулу, должны вычисляться для сечения, в котором действует наибольшая перерезывающая сила. Однако ввиду того, что отношение S/I для различных сечений корпуса изменяется значительно меньше

---

, чем величины S и I в отдельности, допускается подставлять значения S и I, вычисленные для миделевого сечения по результатам первого приближения. Величина статического момента S для половины сечения корпуса и касательные напряжения вычисляется в таблице 11.5. На рисунке 11.5 представлена схема распределения касательных напряжений при общем изгибе.

Таблица 11.5 – Расчет касательных напряжений

Наименование связей	размеры связей см	площадь связи,см2	отстояние от НО, м	Стат.момент см2 м	ΣΣ,см2 м	Касательное напряжения, Мпа
настил ВП	1020х1,2	918	6,432	5904,58	5904,6	28,21
карлингс	56х1,4	78,4	6,122	479,965	12289,1	50,32
палубный стрингер	154х1,4	215,6	6,529	1407,65	14176,7	58,05
ширстрек	154х1,3	2248,2	5,752	12931,65	28516	125,74
ботовой стрингер	56х1,4	78,4	2,092	164,01	41611,7	170,38
борт	637х1,1	700,7	3,185	2231,73	44007,4	229,33

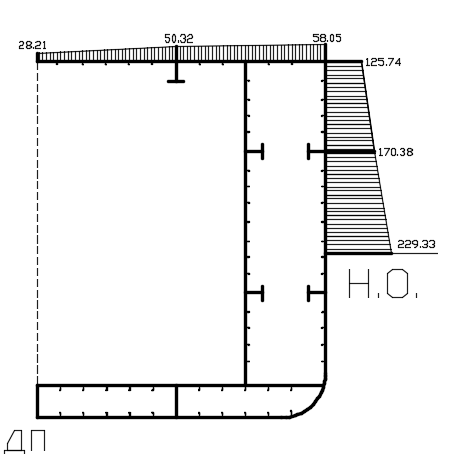
Рисунок 10.2 – Схема распределения касательных напряжений

---

10.5 Проверка прочности корпуса по правилам Регистра

Требования Правил распространяются на суда длиной L ≥ 65м, имеющих:

• 
  соотношения главных размерений L/B ≥5 и B/D ≤2,5;
  
• 
  коэффициент общей полноты Cb>0,6;
  
• 
  спецификационную скорость V_С, превышающую V=k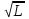 [уз].
  

Расчетные нагрузки, определяющие продольную прочность судна, включают изгибающие моменты и перерезывающие силы на тихой воде, волновые изгибающие моменты и перерезывающие силы, а для судов с большим развалом бортов — изгибающие моменты, обусловленные ударом волн в развал бортов.

Расчетные волновые и ударные нагрузки могут определяться по формулам, приведенным в Правилах и по методикам с учетом качки на волнении, долговременного распределения волновых режимов и районов плавания.

Положительными считаются:

• 
  перерезывающие силы, направленные вниз;
  
• 
  изгибающие моменты, вызывающие перегиб корпуса;
  
• 
  поперечные нагрузки, направленные вниз.
  

Сравнение полученных моментов сопротивления палубы и днища со значениями по правилам Регистра.

Волновой изгибающий момент М_w [кН∙м], действующий в вертикальной плоскости, в рассматриваемом сечении:

• 
  при перегибе судна
  

• 
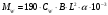
  при прогибе судна
  

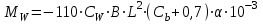
где 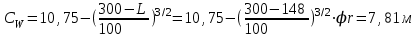при 90
Т.к. максимальный изгибающий момент находится на миделе, т.е. 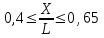, то коэффициент α = 1.

Таким образом, волновой изгибающий момент:

• 
  при перегибе судна
  

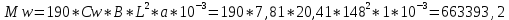кН∙м

• 
  при прогибе судна
  

---

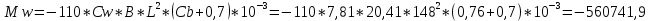кН∙м

Волновая перерезывающая сила N_sw [кН] в рассматриваемом сечении:

• 
  положительная
  

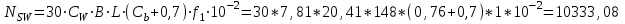кН

• 
  отрицательная
  

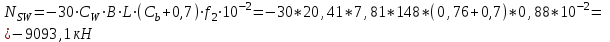
где f₁=1

f₂= 0,88

Расчетный изгибающий момент на тихой воде не должен быть менее



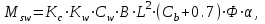
В расчете принять K_w = 0,076 ; Ф = 1; K_c = 1; a = 1; C_b > 0,6– коэффициент общей полноты; C_w– волновой коэффициент, м.



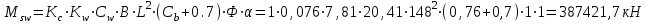
Момент сопротивления рассматриваемого поперечного сечения корпуса (для палубы и днища) W [см³] должен быть не менее



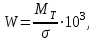
где 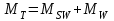– расчетный изгибающий момент [кН∙м] в рассматриваемом сечении, равный максимуму абсолютной величины алгебраической суммы моментов :

• 
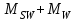  при перегибе судна |Msw+Mw|=|387421,7+663393,3|= 1050815 кН∙м
  
• 
  при прогибе судна |Msw+Mw|=|387421,7+560741,9|= 948163,6 кН∙м
  

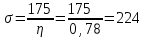МПа,

где η – коэффициент использования механических свойств стали. Для стали D32 — η = 0,78 МПа.

Как видно при перегибе возникает максимальный расчетный изгибающий момент.

Момент сопротивления поперечного сечения корпуса:





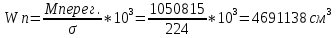
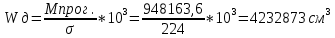
Wп.норм= 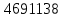см³

Wд.норм= 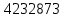см³

Момент сопротивления корпуса для наибольшего расчетного изгибающего момента должен сохраняться постоянным в средней части судна (в пределах 0,4L). Момент сопротивления должен плавно уменьшаться к оконечностям судна за пределами части судна, в которой он сохраняется постоянным.

---