Файл: Практикум волгоград 2014 Печатается по решению редакционноиздательского совета.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 11.12.2023

Просмотров: 249

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

1.2. Закон Бугера

Соответственно, изменение интенсивности света будет равно

dI= –SdP= –P0 Ndz. (23)

2. Описание установки

ИНТЕРФЕРЕНЦИЯ СВЕТА Лабораторная работаИНТЕРФЕРЕНЦИЯ СФЕРИЧЕСКИХ ВОЛН(БИПРИЗМА ФРЕНЕЛЯ)ЦЕЛЬ РАБОТЫ: изучение явления двухлучевой интерференции с помощью бипризмы Френеля, определение длины световой волны с использование данной интерферометрической схемы.ПРИНАДЛЕЖНОСТИ: маломощный непрерывный лазер, две линзы (собирающая и рассеивающая), бипризма Френеля, экран, линейка, оптическая скамья с набором рейтеров.1. Теоретическая часть [1¸6]1.1. Интерференция волнВ эксперименте возможна ситуация, когда интенсивность света, создаваемая какими-либо двумя источниками, не равна сумме интенсивностей отдельных источников. Оказывается, что если свет от одного источника разделить прибором на два пучка и заставить их проходить разные пути, а затем наложить их друг на друга, то интенсивность их в области суперпозиции пучков будет изменяться от точки к точке. Она может достигать максимума, превышающего сумму интенсивностей пучков, и минимума, который может оказаться равным нулю. Это явление называется интерференцией. Оказывается, что при суперпозиции пучков строго монохроматического света интерференция возникает всегда. Однако, свет от физических источников никогда не бывает строго монохроматическим. Как следует из теории излучения атома, его амплитуда и фаза флуктуируют непрерывно и так быстро, что ни глаз, ни быстрый физический детектор не могут уследить за их изменениями. Если две световых волны происходят от одного источника, то возникающие в них флуктуации амплитуды и фазы, вообще говоря, коррелированы, и о таких волнах говорят, что они полностью или частично когерентны, в зависимости от того, будет ли эта корреляция полной или частичной. В общем случае колебания (или волны) называются когерентными, если разность их фаз остается постоянной (или изменяется по определенному закону) во времени. В световых пучках от разных источников флуктуации совершенно независимы и пучки, как говорят, взаимно некогерентны. При наложении таких пучков от независимых источников интерференция в обычных экспериментальных условиях не наблюдается. Детальный анализ показывает, что «степень корреляции» между флуктуациями в двух световых пучках определяет «четкость» интерференционных эффектов, возникающих при суперпозиции пучков и, наоборот, «степень корреляции» сама определяется этими эффектами. Рис.1Рассмотрим вначале классическую схему Юнга наблюдения интерференционной картины для простейшего случая двух гармонических волн. Пусть два точечных источника S1 и S2 , расположенных на расстоянии 2l друг от друга излучают две монохроматические сферические когерентные волны и (рис.1). Предположим, что расстояние D от источников до экрана значительно больше 2l и положим для простоты, что амплитуды волн E1и E2в точке Р одинаковы и равны Е0 . Найдем результирующую амплитуду волн в точке Р, если (1)Тогда суммарная волна в точке Р: . (2)Введем величину , называемую геометрической разностьюхода. Тогда интенсивность света будет равна: . (3)Видим, что при ; (4) при . (5)Таким образом, в результате наложения двух когерентных волн мы будем наблюдать в пространстве (или на экране, как это делается в эксперименте) чередующуюся в зависимости от разности хода картину максимумов и минимумов, называемую интерференционными полосами. 1.2. Получение когерентных световых волн с помощью бипризмы ФренеляДля получения когерентных световых волн от реальных источников пользуются следующим искусственным приемом. Волновой фронт разделяют на несколько частей. Полученные таким образом волны проходят различные оптические пути и при дальнейшем сложении уже обладают разностью хода, оставаясь когерентными. Потому, что разность хода зависит только от конструкции прибора. Рис.2На рис. 2 приведен способ деления фронта волны на две части с помощью бипризмы Френеля. Важно отметить, что в практических приборах разность хода не делается обычно больше 100 ¸ 200 мм, т.к. длительность излучения атома 10-8 с, и при большой разности хода может случиться, что будут складываться волны, полученные уже от разных актов испускания, т.е. когерентность нарушится. Бипризма Френеля имеет малые преломляющие углы (a = 30/ ) и разность хода, приобретаемая волнами здесь мала. После преломления в бипризме падающий пучок света разделяется на два когерентных пучка с источниками в мнимых изображениях S‘ и S“ источника S (рис.3). Вычислим разность хода волн, приходящих в точку Р, через геометрические размеры оптической схемы. . (6)Считая, что в практических схемах d » D, ОР = y«D и следовательно: , получим: Рис.3 (7)Преобразуя (7), получим: (8)Пользуясь условием (4), при котором получается максимум интенсивности на экране, находим: ; (9) . (10)Соотношение (10) показывает, что максимумы отстоят друг от друга на равных расстояниях. Обозначая расстояние, соответствующее одному из максимумов ym, а следующему ym+1, получим: . (11) 2. Описание установки2.1. Определение длины световой волны с помощью бипризмы ФренеляЛабораторная установка (рис.4) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), короткофокусной собирающей линзы с фокусным расстоянием f1= 1 см (3), бипризмы Френеля (4) и экрана (5). Все элементы установлены на оптической скамье (6). Рис. 4. Схема лабораторной установки2.2. Получение увеличенного изображения интерференционной картины Рис. 5. Схема лабораторной установки Лабораторная установка (рис.5) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), короткофокусной собирающей линзы (3) с фокусным расстоянием f1= 1 см, бипризмы Френеля (4), рассеивающей линзы (5) с фокусным расстоянием f2= -11 см, и экрана (6). Все элементы установлены на оптической скамье (7). Линзы закреплены в оправах и устанавливаются в рейтеры, которые могут перемещаться вдоль оптической скамьи. Положение всех элементов на скамье определяется с помощью шкалы, прикрепленной к оптической скамье, или линейки. Все оптические детали центрируются, т.е. должны быть установлены так, чтобы их центры лежали на одной высоте, оптические оси линз были параллельны ребру оптической скамьи, плоскость экрана была перпендикулярна оптической оси линз. 3. Порядок выполнения работы3.1. Установить оптические элементы согласно рис.4. Включить лазер.3.2. Съюстировать линзу (3) по лучу лазера. Луч должен проходить вдоль главной оптической оси линзы. Это можно проконтролировать по отражению от поверхности линзы: отраженный луч должен попадать в выходное отверстие лазера. При этом лазерный пучок собирается в точку в фокальной плоскости.3.3. Установить бипризму на расстоянии a 8–10 см от точки фокуса линзы. Расположить ее так, чтобы ребро бипризмы находилось в середине расфокусированного пятна.3.4. Установить экран на расстоянии b 100 см от бипризмы. На экране будет наблюдаться интерференционная картина, образованная двумя когерентными пучками, идущими от мнимых источников, расстояние l между которыми вычисляется по формуле: , (12)где a - угол между преломляющей гранью и основанием бипризмы (a = 20/ = 5,8.10-3 рад). Измерить ширину интерференционной полосы Dy (расстояния между соседними максимумами) не менее трёх раз. С целью увеличения точности измерения Dy нужно определять расстояние между максимально удаленными друг от другаi-й и k-й интерференционными полосами и делить его на . По формуле: (13)определить длину волны l излучения лазера для различных значений Dy.3.7. Провести статистическую обработку результатов с доверительной вероятностью 90%.3.8. Установить оптические элементы согласно рис.5. Получить увеличенную интерференционную картину. Ширина интерференционной полосы при наличии рассеивающей линзы будет определяться выражением: , (14)где x - расстояние между мнимыми источниками и рассеивающей линзой, D - расстояние между экраном и мнимыми источниками. Измерить Dy’ при разных положениях линзы не менее трёх раз.3.9. Определить из формулы (14) длину волны лазера для различных значений Dy’. Провести статистическую обработку результатов с доверительной вероятностью 90%.3.10. Сравнить полученный результат с истинной длиной волны лазера и со значением, полученным в п.3.7. 4. Контрольные вопросы и задания В чем состоит классический опыт Юнга по наблюдению интерференционной картины? Из какого условия находятся минимальные и максимальные значения интенсивности на экране для этого случая? Что называется интерференцией? В результате интерференции каких волн получается четкая интерференционная картина? Как связаны между собой когерентность и монохроматичность световых волн? Может ли наблюдаться интерференционная картина в солнечном свете? Какие существуют способы получения когерентных волн в оптике? Объясните принцип действия билинзы Бийе, бизеркал Френеля, зеркала Ллойда? Точечный монохроматический источник света (l = 0,5 мкм) расположен на оси симметрии бипризмы Френеля, перпендикулярной наибольшей стороне, на расстоянии 0,1 м от бипризмы, а плоский экран находится на расстоянии 2,9 м от бипризмы. Сколько белых и темных полос образуется на экране (угол a при вершине бипризмы составляет 20’, толщиной бипризмы в расчетах можно пренебречь)? Найдите распределение интенсивности на экране в установке с зеркалами Френеля. Интерферирующие лучи падают на экран приблизительно перпендикулярно его поверхности. Найдите ширину полос интерференции в установке с зеркалом Ллойда, если известна длина волны излучения, расстояние от вторичных источников до экрана и расстояние от источника до зеркала. Лабораторная работаКОЛЬЦА НЬЮТОНАЦЕЛЬ РАБОТЫ: изучение явления интерференции в тонких клиньях с помощью колец Ньютона (полосы равной толщины), определение радиуса кривизны линзы и длины световой волны с помощью такой интерференционной схемы.ПРИНАДЛЕЖНОСТИ: маломощный непрерывный лазер, ртутная лампа, оптическая скамья, набор светофильтров, микроскоп, волоконный световод, система «линза-пластинка» для наблюдения колец Ньютона.1. Теоретическая часть [1¸6]1.1. Виды интерференционных полосПроисхождение интерференционной картины и способ ее получения определяют вид интерференционных полос, представляющих собой чередующиеся максимумы и минимумы интенсивности света.Пусть интерференционное устройство представляет собой слой прозрачного диэлектрика с частично отражающими и пропускающими поверхностями, в котором возникает геометрическая разность хода D при произвольном угле падения j света на это устройство. К такому типу интерферометров можно отнести плоскопараллельные и клиновидные диэлектрические пластины (например, интерференция в тонких пленках, кольца Ньютона и др.), а также интерферометры, расщепляющие пучки с помощью зеркал (интерферометр Майкельсона и его аналоги, эталон Фабри-Перо). Здесь можно рассмотреть три вида интерференционных полос, получающихся при следующих условиях: l = const; j = const. При вариации геометрической разности хода имеют место полосы равной толщины. l = const; D = const. При вариации угла падения получаем полосы равного наклона. j = const; D = const. При вариации длины волны получаем полосы равного хроматического порядка. Полосы равной толщины возникают в том случае, если интерферирующие пучки после прохождения интерференционной системы имеют реальное или мнимое пересечение в пространстве изображений.Полосы равного наклона возникают между параллельными пучками света, которые после прохождения интерферометра приобретают определенную разность хода.Полосы равного хроматического порядка в интерференционных схемах используется крайне редко (для очень точных измерений толщины плоскопараллельных пластин или воздушных промежутков). 1.2. Интерференция в тонких пленкахПри распространении световой волны в среде уменьшается скорость распространения волны и соответственно ее длина, т.к. частота не изменяется. При расчете изменения фаз волны в среде в качестве длины пути удобнее брать оптическую длину пути, равную геометрической длине, умноженной на показатель преломления: . (1)Тогда длину волны и волновой вектор в формулах можно задавать равными их значениям в вакууме. Аналогично (1) вводится и связь между геометрической и оптической разностью хода. Рис.1Полосы равного наклона. Рассмотрим случай, когда плоская монохроматическая волна падает под углом j на поверхность плоскопараллельной пластинки с относительным показателем преломления n и толщиной h(рис.1). Интерференция возникает между двумя волнами, отраженными от верхней и нижней поверхностями пластины. Так как эти пучки параллельны между собой, то интерференция наблюдается (локализована) или на бесконечности, или в фокальной плоскости Fлинзы Л. С учетом потери полволны на границе раздела сред (если n> 1, то в точке A, если n< 1, то в точке B) оптическая разность хода в данном случае равна . (1)Проведем ряд несложных преобразований для нахождения оптической разности хода. . (2)Тогда . (3)Далее, . (4)Но . (5)Поэтому . (6)Тогда: (7)Здесь учтена связь из закона Снеллиуса углов падения j и преломления q: . (8)Таким образом, получаем для оптической разности хода: . (9)Условием максимума интерференционной картины является (см. лабораторную работу «Бипризма Френеля»: . (10)а условием минимума – (11)Если на пластинку падают непараллельные пучки света, то и интерферирующие пучки будут иметь все всевозможные направления распространения. При заданных толщине пластины и показателе преломления каждому углу падения волны соответствует своя интерференционная полоса. Поэтому такие полосы и называют полосами равного наклона. При аксиально симметричном распределении падающих пучков линии равного наклона являются окружностями.Даже если источник света протяженный, и различные его точки излучают некогерентно, интерференционные картины не зависят от фазы волны в точке расщепления пучков на поверхности пластины (точка A на рис.1) и от положения этой точки, а зависят лишь от угла падения. Поэтому конечность размеров источника не смазывает картину полос равного наклона и не является ограничивающим интерференцию фактором.Если падающий свет не монохроматичный, при увеличении разности длин падающих волн интерференционные кольца разделяются и при некотором значении этой разности полосы соседних порядков перекрываются. Разность длин волн, при которой наступает перекрытие полос соседних порядков интерференции, называется дисперсионной областью(или областью свободной дисперсии). Увеличение толщины пластины уменьшает дисперсионную область. Для наблюдения интерференции в белом свете толщина должна быть достаточно малой (

ДИФРАКЦИЯ СВЕТА Лабораторная работаЗОНЫ ФРЕНЕЛЯЦЕЛЬ РАБОТЫ: изучение дифракции Френеля на круглом отверстии и свойств зонной пластинки.ПРИНАДЛЕЖНОСТИ: маломощный непрерывный лазер, металлическая пластинка с набором круглых отверстий различных диаметров, две собирающие линзы, зонная пластинка, экран, линейка, оптическая скамья с набором рейтеров. 1. Теоретическая часть [1¸6] 1.1. Принцип Гюйгенса-ФренеляПод дифракцией света обычно понимают отклонения закономерностей распространения света от законов, предписываемых геометрической оптикой. В явлениях дифракции, как и в явлениях интерференции, проявляются волновые свойства света. Дифракцию можно наблюдать, например, когда на пути распространения света находятся препятствия, т.е. непрозрачные тела произвольной формы (экраны) или когда волновой фронт искусственно ограничен. Тщательный опыт показывает, что вместо резкой границы между светом и тенью (как предсказывает геометрическая оптика) получается сложная картина распределения освещенности, состоящая из темных и светлых участков – дифракционных полос. Теория дифракции света дает строгое обоснование геометрической оптике и определяет условия ее применимости. Математически строгое решение дифракционных задач на основе волнового уравнения (или уравнений Максвелла) с граничными условиями, зависящими от характера препятствий, как правило, представляет значительные трудности. Поэтому применяются приближенные методы решения задачи о распределении света вблизи границы между светом и тенью, основанные на принципе Гюйгенса – Френеля.Пусть A – источник света, а s – произвольная замкнутая поверхность, охватывающая A. Согласно принципу Гюйгенса – Френеля,в любой точке, находящейся вне поверхности s, световая волна, возбуждаемая источником A, может быть пред­ставлена как результат суперпозиции когерентных вторичных волн, которые «излучаются» элементарными источниками, непрерывно рас­пре­де­лен­ными вдоль вспомогательной поверхности s. Иными словами, вне поверхности s распространяющаяся пер­вич­ная волна может быть заменена системой когерентных вторичных волн, интерферирующих при наложении [1]. Принцип Гюйгенса-Френеля является приближением, наиболее пригодным для описания дифракции коротких волн (когда длина волны много меньше характерных размеров препятствий). При формулировке принципа не уточняются граничные условия для напряженностей электромагнитного поля (например, не различаются металлический и диэлектрический экраны) и не учитывается векторный характер поля. Для решения задач по нахождению распределения интенсивности света при дифракции на непрозрачных экранах с отверстиями делаются два предположения (граничные условия Кирхгофа) [2]: непроницаемые части экрана не являются источниками вторичных волн; в отверстии точки волнового фронта являются такими же источниками вторичных волн, какими они были бы при отсутствии непроницаемых частей экрана. 1.2. Зоны Френеля [2] Рис. 1 Пусть A – источник сферической волны, S – волновой фронт в некоторый момент времени, R – радиус кривизны этого фронта (рис.1). Найдем интенсивность в точке P с помощью принципа Гюйгенса – Френеля. Разобьем поверхность S на кольцеобразные зоны такого размера, чтобы расстояния от краев зоны (в разрезе это соответствует точкам M1 ,M2 , …, Mm) до P отличались на l/2 (эти зоны называются зонами Френеля): (1)Из рис.1 видно, что радиус m–й зоны Френеля rm (m=0;1;2;…) может быть получен из соотношения: (2)Исключая величину dm и пренебрегая слагаемыми l2 ввиду их малости, получаем: (3)Можно показать, что площади всех зон Френеля примерно одинаковы: (4)В случае пренебрежения кривизной поверхности это не вносит существенной ошибки, если радиусы зон Френеля много меньше радиуса кривизны волнового фронта. Обычно это справедливо для очень большого числа зон Френеля. 1.3. Метод векторных диаграммРазделим каждую из зон, в свою очередь, на большое число N участков. Между началом и концом зоны фаза меняется на p, а между малыми участками – на d = p/N . Пусть E0 – амплитуда волны, приходящей в точку наблюдения P от каждого участка; а фаза волны, приходящей из точки D в точку P – равна нулю. Комплексная амплитуда волны в точке P от центральной зоны Френеля с учетом интерференции равна: Рис. 2 (5)Аналитическое сложение амплитуд можно заменить графическим построением, изображая комп­лекс­ную амплитуду в виде вектора (рис.2). При увеличении числа разбиений до бесконечности ломаная кривая превращается в плавную. Длина вектора DM1 пропорциональна амплитуде вол­ны в точке P, когда открыта вся центральная зона Френеля. Аналогично продолжая построение, можно получить кривую, по которой легко определить амплитуду волны (и ее интенсивность), зная соотношение диаметров открываемого отверстия и зон Френеля. При строгом равенстве амплитуд в (5) складываемых колебаний от элементарных участков результирующая амплитуда от двух открытых соседних зон была бы равна нулю, т.е. вторичные волны в результате интерференции погасили бы друг друга, но увеличение номера зоны приводит к уменьшению амплитуд вторичных волн (например, в (4) мы этим пренебрегли). Поэтому полученная кривая не замыкается, а имеет вид спирали. Зависимость амплитуды поля в точке P от радиуса отверстия показана на рис.3. Рис. 3 Если на пути световой волны стоит непрозрачный круглый экран, то за экраном в его тени на оси возникает светлое пятно, называемое пятном Пуассона. Объяснение существования светлого пятна вытекает из рассуждений по методу зон Френеля. Экран закрывает некоторое число зон Френеля начиная с центральной. Однако следующие зоны после последней из закрытых создают в точке P освещенность, значение которой можно рассчитать с помощью спирали. Т.о., получается, что волна как бы огибает непрозрачный экран. Интенсивность пятна Пуассона весьма слаба при больших размерах непрозрачного экрана. Кроме того, необходимо, чтобы свет обладал достаточно большой степенью когерентности. 1.4. Зонная пластинка Закроем все нечетные зоны, оставив открытыми четные (или наоборот). В результате получится пластинка, называемая зонной пластинкой. Из рис. 2 видно, что амплитуды поля в точке P будут определяться суммой сонаправленных векторов и т.д. Следовательно, в точке P на оси происходит значительное увеличение интенсивности света по сравнению с интенсивностью в точке P при полностью открытом фронте (примерно в m2 большее, чем дает отверстие в одну зону [3] ), т.е. в этой точке свет фокусируется, а зонная пластинка ведет себя как линза. Найдем фокусное расстояние f такой линзы. Будем считать, что лучи падают на зонную пластинку параллельно оси системы, т.е. R= ¥. Тогда точка P является фокусом. Формула (3) примет вид: (6)Следовательно фокусное расстояние равно: (7)Формула такой линзы принимает вид: (8)т.е. аналогична известной формуле тонкой линзы. В отличие от обычной линзы зонная пластинка имеет несколько фокусов на оси системы в зависимости от количества открытых зон. Отметим, что и расположение зон Френеля на волновом фронте зависит от геометрии рассматриваемой системы. 2. Описание установки 2.1. Дифракция Френеля на круглом отверстии Рис. 4. Схема лабораторной установки Лабораторная установка (рис.4) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), короткофокусной собирающей линзы (3) с фокусным расстоянием f1 = 1 см, металлической пластинки (4) с отверстиями диаметрами 1,59; 1,40; 1,13; 0,85; 0,71; 0,50 мм и экрана (5). Все элементы установлены на оптической скамье (6). 2.2. Изучение свойств зонной пластинки Рис. 5. Схема лабораторной установки Лабораторная установка (рис.5) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), короткофокусной собирающей линзы (3) с фокусным расстоянием f1= 1 см, длиннофокусной собирающей линзы (4) с f2= 21 см, зонной пластинки (5) и экрана (6). Все элементы установлены на оптической скамье (7). Линзы закреплены в оправах и устанавливаются в рейтеры, которые могут перемещаться вдоль оптической скамьи. Положение всех элементов на скамье определяется с помощью шкалы, прикрепленной к оптической скамье, или линейки. Все оптические детали центрируются, т.е. должны быть установлены так, чтобы их центры лежали на одной высоте, оптические оси линз были параллельны ребру оптической скамьи, плоскость экрана была перпендикулярна оптической оси линз.3. Порядок выполнения работы3.1. Установить оптические элементы согласно рис.4. Включить лазер.3.2. Съюстировать линзу (3) по лучу лазера. Луч должен проходить вдоль главной оптической оси линзы. Это можно проконтролировать по отражению от поверхности линзы: отраженный луч должен попадать в выходное отверстие лазера. При этом лазерный пучок собирается в точку на фокальной плоскости.3.3. Установить металлическую пластинку с отверстиями на расстоянии 5 – 25 см от точки фокуса линзы. Расположить одно из отверстий в центр расфокусированного пятна. 3.4. Установить экран на расстоянии 50 – 100 см от фокальной плоскости линзы. На экране будет наблюдаться дифракционная картина.3.5. Передвигая экран, добиться появления в центре дифракционной картины светлого пятна. Для данного положения измерить расстояния от фокальной плоскости линзы до отверстия R1 и от отверстия до экрана L1 . Число открытых зон Френеля k1 определяется из (3) выражением: (9)где a – диаметр отверстия, l – длина волны излучения лазера.3.6. Плавно перемещая пластинку с отверстием вдоль оси системы, найти ближайшее положение, когда в центре дифракционной картины появится темное пятно. Переход от светлого пятна к темному (или наоборот) соответствует изменению числа открытых зон Френеля на единицу.3.7. Передвигая пластинку с отверстием дальше, определить общее число таких изменений Dk (желательно 3 – 5). Измерить расстояния R2 и L2 для конечного положения экрана. Для этого положения можно записать: (10)3.8. По формуле (11)определить длину волны l излучения лазера.3.9. Повторить п.п.3.3 – 3.8. для всех отверстий.3.10. Провести статистическую обработку результатов с доверительной вероятностью 90%. Сравнить полученный результат с истинной длиной волны лазера.3.11. Установить оптические элементы согласно рис.5, но без зонной пластинки. 3.12. Съюстировать линзы по лазерному лучу. Расположить линзы так, чтобы они образовали телескопическую систему. Фокусы линз при этом совпадают. На выходе такого телескопа должен получиться широкий параллельный пучок света. Проверить параллельность этого пучка: диаметр пучка не должен изменяться с изменением расстояния от телескопа.3.13. Установить на оптическую скамью между телескопом и экраном зонную пластинку так, чтобы пучок света падал в центр зонной пластинки нормально поверхности.3.14. Перемещая экран вдоль оптической оси, зафиксировать положение, при котором в центре дифракционной картины наблюдается яркая точка. Измерить расстояние L от пластинки до экрана. Это измерение даст значение главного фокусного расстояния f0 зонной пластинки.3.15. Передвигая экран, зафиксируйте остальные фокусы fm зонной пластины. Фокусные расстояния fm и главное фокусное расстояние f0 связаны соотношением: (12)(В данном эксперименте удается измерить фокусные расстояния лишь при m = 0 и 1).3.16. Повторите пп.3.14 – 3.15 пять раз. Усредните полученные результаты.3.17. Сравните экспериментально полученные значения fm и рассчитанные по формуле (12).4. Контрольные вопросы и задания Что понимается под дифракцией света? Можно ли отнести явление миража к дифракционному явлению? Сформулируйте принцип Гюйгенса-Френеля. В чем заключаются допускаемые приближения? Изложите метод зон Френеля и проведите на его основе анализ полученных в данной лабораторной работе результатов при дифракции световых волн на круглом отверстии. Освещенность в точке P за круглым отверстием, открывающим одну зону Френеля, примерно в четыре раза больше, чем при полностью открытом волновом фронте. Если увеличить вдвое площадь отверстия, освещенность в точке P уменьшится почти до нуля, несмотря на удвоение светового потока. Как эти факты согласовать с законом сохранения энергии? Получите выражение для зонной пластинки и докажите ее фокусирующее действие. Увяжите эти результаты с фокусирующим действием линзы. В чем заключается метод векторных диаграмм в применении к задачам дифракции? Почему интенсивность в фокусах зонной пластинки максимальна для самого дальнего от пластинки фокуса? Объясните возникновение светлого пятна в центре тени от круглого диска при освещении последнего светом. В каких условиях можно обнаружить это пятно? Покажите с помощью векторной диаграммы, что освещенность в центре геометрической тени круглого диска, перекрывающего небольшое число зон Френеля, почти такая же, как и в освещенной области. Как качественно зависит интенсивность пятна Пуассона от расстояния до непрозрачного экрана? Во сколько раз интенсивность в главном фокусе зонной пластинки больше, чем в фокусе n-го порядка? Диск диаметром 5 мм, имеющий неровности порядка 10 мкм, расположен на расстоянии 1 м от точечного монохроматического источника света, излучающего на длине волны 0,5 мкм. Точечный источник находится на перпендикуляре к плоскости диска, проходящем через его центр. Считая, что пятно Пуассона видно лишь до тех пор, пока неровности краев диска перекрывают соответствующую зону Френеля не более чем на 1/4 ее ширины, найти минимальное расстояние, на котором можно видеть пятно Пуассона. Точечный источник монохроматического света расположен на расстоянии R от круглого отверстия, а экран­ – с противоположной стороны на расстоянии L. При каких значениях радиуса r отверстия центр наблюдаемых на экране дифракционных колец будет светлым, а при каких – темных? Точечный монохроматический источник света (l = 0,5 мкм) расположен на расстоянии 0,5 м от плоского экрана с круглым отверстием диаметром 0,5 мм на перпендикуляре к плоскости экрана, проходящей через центр отверстия. На каком расстоянии от отверстия на перпендикуляре расположена точка, имеющая максимум освещенности? Какова будет интенсивность света I в фокусе зонной пластинки, если закрыть всю пластинку, за исключением верхней половины первой зоны? Интенсивность света без пластинки равна I0. Какова интенсивность света I в центре дифракционной картины от круглого экрана, если он закрывает всю первую зону? Интенсивность света в отсутствие экрана равна I0. Монохроматический точечный источник расположен на оси зонной пластинки на расстоянии R от нее. Наиболее яркое изображение источника получается на расстоянии L от пластинки. На каких расстояниях получаются другие изображения источника? Лабораторная работаДИФРАКЦИЯ ФРАУНГОФЕРАЦЕЛЬ РАБОТЫ: изучение дифракции Фраунгофера на одной щели, на двух щелях и амплитудной дифракционной решетке.ПРИНАДЛЕЖНОСТИ: маломощный непрерывный лазер, раздвижная щель типа спектральной щели, пластина с двумя близко расположенными прозрачными щелями, амплитудная дифракционная решетка, экран, линейка, оптическая скамья с набором рейтеров. 1. Теоретическая часть 1.1. Область дифракции ФраунгофераЯвления дифракции принято классифицировать в зависимости от расстояния источника и точки наблюдения (экрана) до препятствия, поставленного на пути распространения света, а также длины волны дифрагирующего излучения. Обычно рассматривают два типа дифракции – Фраунгофера и Френеля. Проведем разграничение этих типов на примере дифракции световой волны на круглом отверстии радиуса R. В оценке этого разграничения основную роль будет играть отношение площади центральной зоны Френеля (см. лабораторную работу «Зоны Френеля») к площади отверстия. Площадь центральной зоны Френеля приближенно можно оценить из формулы, в которой учтено, что расстояние от источника света до отверстия a1 по порядку величины совпадает с расстоянием a2от отверстия до плоскости наблюдения дифракционной картины: (1)где L a1 a2, l – длина волны света.Площадь отверстия радиуса R равна (2)Введем величину D, равную отношению этих двух площадей и называемую волновым параметром: (3)Волновой параметр играет большую роль в задачах дифракции. Можно выделить три случая: D << 1. Отверстие имеет размеры много больше размеров центральной зоны Френеля. В этом случае – случае большого отверстия (или очень малых длин волн) – выявить дифракционные, т.е. волновые проявления света достаточно трудно и можно говорить о соблюдении законов геометрической оптики. D 1. При этом условии дифракционные эффекты начинают играть существенную роль. Например, если отверстие совпадает с центральной зоной Френеля, то интенсивность света в центре дифракционной картины в 4 раза больше интенсивности света в той же точке, создаваемой полностью открытым фронтом. Этот случай соответствует дифракции Френеля. D >> 1. Размеры препятствия много меньше размеров центральной зоны Френеля. Этот случай наблюдается или при очень больших длинах волн (как правило, это соответствует радиодиапазону), или при большом удалении источника света от препятствия, когда можно считать, что на препятствие падает практически плоская волна. Поэтому этот случай называется дифракцией в параллельных лучах, дифракцией в дальней зоне или чаще дифракцией Фраунгофера. Именно дифракция Фраунгофера играет основную роль для расчетов большинства оптических приборов. Практически для осуществления дифракции Фраунгофера точечный источник монохроматического света помещают в фокусе собирающей линзы (коллиматора), тогда на препятствие после коллиматора падает практически параллельный пучок света. Или в качестве источника плоской монохроматической волны используют лазер, который имеет малую расходимость пучка, например, гелий-неоновый (He-Ne) лазер. Дифракционная картина наблюдается, в общем случае, на бесконечности или на фокальной плоскости линзы, установленной после препятствия (часто для наблюдения используют зрительную трубу, установленную «на бесконечность»). При достаточно малых размерах препятствий (начиная с 0,1 мм для видимого диапазона дифрагирующих волн) дифракционная картина хорошо наблюдается и на коротких расстояниях (

ПОЛЯРИЗАЦИЯ СВЕТА

Преломленная волна частично поляризована. Соотношение

ОПТИЧЕСКИЕ СПЕКТРАЛЬНЫЕ ПРИБОРЫ

ПОЛЯРИЗАЦИЯ СВЕТА


Лабораторная работа

ЛИНЕЙНЫЙ ЭЛЕКТРООПТИЧЕСКИЙ ЭФФЕКТ

(ЭФФЕКТ ПОККЕЛЬСА)
ЦЕЛЬ РАБОТЫ: изучение линейного электрооптического эффекта и закономерностей прохождения поляризованного света через анизотропную среду.
ПРИНАДЛЕЖНОСТИ: маломощный непрерывный лазер, электрооптический модулятор, источник питания модулятора, поляризатор, фотоприемник, оптическая скамья.
1. Теоретическая часть
Электрооптический эффект состоит в изменении показателя преломления среды под действием электрического поля. Это изменение может быть как первого (линейный электрооптический эффект Поккельса), так и второго (квадратичный электрооптический эффект Керра) порядков относительно приложенного поля.

Изменение показателя преломления среды под действием электрического поля широко используется в лазерной физике и технике. Сюда следует отнести электрооптические затворы для модуляции добротности лазеров, системы сканирования световых пучков, модуляция света в приемо-передающих устройствах систем оптической связи и т.д.
1.1. Распространение света в анизотропной среде [1¸6, 10]
В изотропной среде связь между вектором напряженности электрического поля E и вектором индукции D дается соотношением

(1)

где e – постоянная скалярная величина, не зависящая от направления распространения волны, называемая диэлектрической проницаемостью. Поэтому вектор D совпадает по направлению с вектором E.

В случае анизотропной среды каждая компонента D зависит от величины всех трех составляющих электрического поля E :

(2)

(Индексы i, j=1,2,3 соответствуют декартовым координатам x,y,z.)

Коэффициенты eij являются компонентами тензора второго ранга –тензора диэлектрической проницаемости. Всю совокупность возможных значений диэлектрической проницаемости можно представить при помощи трехосного эллипсоида с осями x, y, z. Значение диэлектрической проницаемости для любого направления выражается длиной радиус-вектора эллипсоида, проведенного по этому направлению. Три значения диэлектрической проницаемости ex, ey, e
z , соответствующие полуосям эллипсоида, называются главными значениями диэлектрической проницаемости.

Используя связь между D и E, характеризующую анизотропию среды, можно решить систему уравнений Максвелла, причем в качестве осей координат удобно выбрать главные направления диэлектрической проницаемости (главные оси кристалла) ([1] ¸ [6]). Распространяющаяся в анизотропной среде электромагнитная волна обладает следующими особенностями [2]:

  1. По заданному направлению r могут распространяться две плоских линейно поляризованных волны с двумя различными фазовыми скоростями, соответствующими двум различным плоскостям колебания электрического вектора волны. Эти две плоскости колебания определяются свойствами кристалла (тензором диэлектрической проницаемости) и всегда взаимно перпендикулярны.




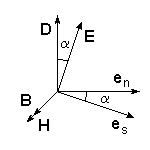
Рис. 1
2. В плоскости волнового фронта, т.е. в плоскости, перпендикулярной r, расположен вектор индукции D и вектор напряженности магнитного поля H, совпадающий по направлению с вектором магнитной индукции B = mH (не будем рассматривать магнитную анизотропию, т.к. она в оптическом диапазоне встречается и используется крайне редко). Вектор же напряженности электрического поля E в анизотропной среде не совпадает с D и образует некоторый угол a (рис.1).
Плоскость фронта волны, распространяющейся вдоль вектора en есть плоскость DH. Плоскость EH, обладающая тем свойством, что перпендикуляр к ней совпадает с направлением энергии световой волны (вектором Пойнтинга), повернута относительно DH на угол a. Таким образом, в анизотропной среде в общем случае направление энергии (луча) es не совпадает с направлением волновой нормали . Совпадение имеет место только в том случае, если en направлено вдоль одного из трех главных осей кристалла.

В оптике обычно имеют дело не с диэлектрической проницаемостью среды, а с показателем преломления n = e1/2 , определяющем фазовую скорость распространения света v = c/n .

Для нахождения показателя преломления в анизотропной среде строят эллипсоид, называемый оптической индикатрисой. Если X,Y,Z – главные оси кристалла, то уравнение оптической индикатрисы имеет вид:

(3)


где – главные показатели преломления среды.




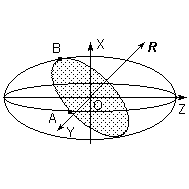
Рис. 2
Оптическая индикатриса имеет следующее важное свойство. Проведем из начала координат прямую OR в произвольном направлении (рис.2). Построив центральное сечение индикатрисы, перпендикулярное этой прямой, получим эллипс. Тогда показатели преломления для двух волн с волновой нормалью OR равны длинам полуосей этого эллипса OA и OB. Направление поляризаций волн совпадает с направлением осей эллипса. Вектор индукции D в плоско поляризованной волне, показатель преломления для которой равен OA, колеблется параллельно OA. Аналогично в волне для которой показатель преломления равен OB, вектор D колеблется параллельно OB. Отсюда, как частный случай, следует, что для волн с волновой нормалью X показатели преломления равны ny и nz, а вектор D в этих волнах параллелен соответственно Y или Z.

Симметрия кристалла налагает определенные требования на форму и ориентацию оптической индикатрисы. Например, для кубических кристаллов симметричными преобразованиями (т.е. такими преобразованиями, после которых кристалл переходит сам в себя) являются повороты относительно всех трех его осей. Отсюда следует, что оптическая индикатриса кубических кристаллов является сферой. Т.к. все центральные сечения индикатрисы в этом случае представляют окружности, эти кристаллы не обладают анизотропией.

Для гексагональных, тетрагональных (к этому классу относятся кристаллы дигидрофосфата калия KH2PO4 (сокращенно KDP)) и тригональных (ниобат лития LiNbO3) кристаллов индикатриса представляет собой эллипсоид вращения вокруг главной оси симметрии. Принимая эту ось за ось z, уравнение индикатрисы можно записать в виде:

(4)

Центральное сечение, перпендикулярное главной оси (и только это сечение), есть окружность радиуса no. Поэтому для света с волновой нормалью, направленной вдоль главной оси
Z, двулучепреломление отсутствует. В направлении, перпендикулярном плоскости кругового сечения, всем волнам соответствует одна и та же скорость, поляризация может быть любой. Направление, перпендикулярное круговому сечению, называется оптической осью кристалла. Для волн, идущих вдоль оптической оси среда ведет себя как изотропная. Такие кристаллы с одним круговым сечением индикатрисы называются одноосными.

Для трех остальных кристаллографических систем (орторомбической, моноклинной и триклинной) индикатриса является трехосным эллипсоидом. Она имеет два круговых сечения. Такие кристаллы называются двуосными.

Плоскость, проходящая через луч, направленный под углом к оптической оси и оптическую ось, называется главной. Из этого определения и определения главной оси следует, что у волны, вектор E которой направлен перпендикулярно главной плоскости, скорость не зависит от направления. Такая волна называется обыкновенной. Соответствующие ее параметры (скорость, показатель преломления) обозначаются индексом “о” (“ordinary”). У волны, вектор E которой лежит в главной плоскости, скорость зависит от направления, т.к. соответствующая полуось эллипса в сечении эллипсоида изменяется с изменением направления волны. Такая волна называется необыкновенной. Соответствующие ей параметры (скорость, показатель преломления) обозначаются индексом “е” (“extraordinary”) . Т.е., показатель преломления необыкновенной волны – величина переменная, зависящая от направления. Значение ne, приводящееся для данного кристалла в справочной литературе – это максимально отличающееся от “обыкновенного” показателя преломления noзначение. Кристалл называется положительным, если ne – no > 0, и отрицательным при ne – no < 0 (кристаллы KDP и ниобата лития являются отрицательными).

Рассмотрим распространение поляризованного излучения в кристаллической пластинке. Линейно поляризованный свет, падая на кристалл, дает начало двум когерентным волнам, распространяющимся с различной скоростью и приобретающим после прохождения пластинки разность фаз, зависящую от толщины кристалла и различия в показателях преломления обеих волн. Так как колебания в этих волнах взаимно перпендикулярны, то они в общем случае ведут к образованию эллиптически поляризованного света. В точках, соответствующих различным разностям хода, форма и ориентация эллипсов могут быть различными, но интенсивность света везде одна и та же. Поместив после кристалла анализатор, мы от каждой волны пропускаем лишь ту компоненту колебания, которая параллельна его плоскости поляризации. Разность фаз между рассматриваемыми волнами на выходе кристаллической пластинки толщиной
l определяется формулой:

(5)

где n1 , n2– показатели преломления для двух волн, l – длина волны света.
1.2. Эффект Поккельса
Эффект Поккельса возможен лишь в кристаллах, не имеющих центра симметрии. В кристаллах, имеющих центр симметрии, возможен только квадратичный эффект Керра.

В результате наложения электрического поля на кристалл происходят поворот и деформация оптической индикатрисы. Если в качестве координатных осей выбрать главные оси кристалла, то в отсутствие электрического поля уравнение оптической индикатрисы можно записать в виде:

(6)

где , а индекс “0” отражает тот факт, что на кристалл не наложено поле.

При наложении электрического поля E = {Ex; Ey; Ez} уравнение индикатрисы принимает вид:

(7)

где коэффициенты aijзависят от поля следующим образом:

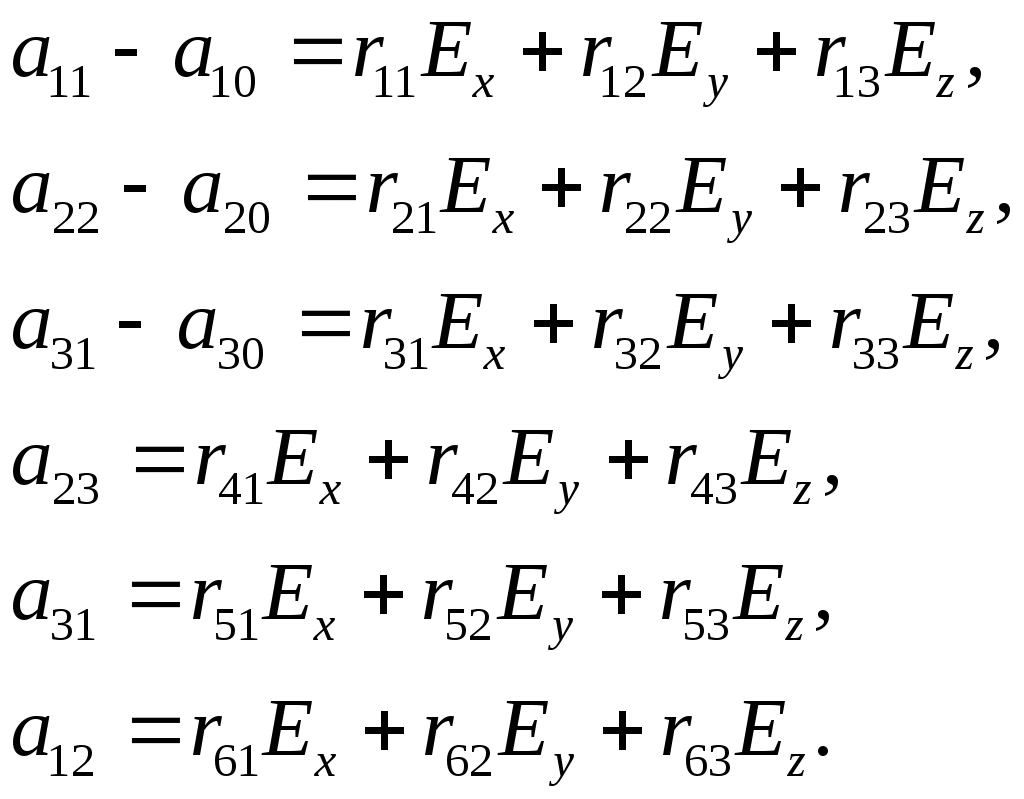(8)

Коэффициенты rij называются электрооптическими коэффициентами, максимальное число их равно 18, однако число отличных от нуля и число независимых электрооптических постоянных значительно меньше и определяется симметрией кристалла.

Рассмотрим электрооптический эффект в кристалле ниобата лития. Это одноосный кристалл (a10 = a20), у которого отличны от нуля следующие электрооптические коэффициенты: r13 = r23; r33; r42 = – r51; r22 = – r12 = – r61 . Уравнение оптической индикатрисы для ниобата лития при произвольном направлении электрического поля имеет вид:

(9)

Видно, что при наличии электрического поля оси эллипсоида x’, y’, z’ не совпадают с исходными кристаллографическими осями x, y, z. Для того, чтобы найти новые направления осей, необходимо привести (9) к каноническому виду.

Рассмотрим наиболее интересный в практическом отношении случай. Пусть электрическое поле перпендикулярно оптической оси

Смотрите также файлы