Файл: Курсовой проект по дисциплине конструкция и прочность авиационных двигателей тема Анализ статической и динамической прочности рабочей лопатки первой ступени турбины гтд тв2117.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 174
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, что частота собственных колебаний не зависит от частоты вращения ротора. При расчёте частот изменения возмущающих сил во внимание следует принимать наиболее существенные газодинамические неоднородности, создаваемые лопатками соплового аппарата первой ступени турбины и форсунками камеры сгорания.
Тогда:
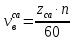– частота возмущающей силы, вызванной наличием сопловых аппаратов, 1/с;
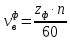– частота возмущающей силы, вызванной наличием форсунок, 1/с;
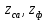– число лопаток соплового аппарата первой ступени турбины и число форсунок в камере сгорания;
n – частота вращения ротора, об/мин.
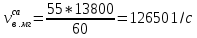
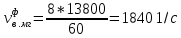
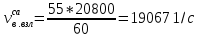
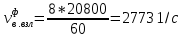
Линии изменения частот возмущающей силы и частот собственных колебаний наносятся на график в координатах
.
В случае близости резонансных точек к границам рабочего диапазона оборотов ротора двигателя определяется запас по частоте вращения.
Если в рабочем диапазоне частот вращения ротора окажутся резонансные точки, то делается вывод о том, что рабочая лопатка не удовлетворяет требованиям динамической прочности.
Линии изменения частот возмущающей силы и частот собственных колебаний наносятся на график (рис.6) в координатах .
В случае близости резонансных точек к границам рабочего диапазона оборотов ротора двигателя определяется запас по частоте вращения.
Если в рабочем диапазоне частот вращения ротора окажутся резонансные точки, то делается вывод о том, что рабочая лопатка не удовлетворяет требованиям динамической прочности.
об/мин
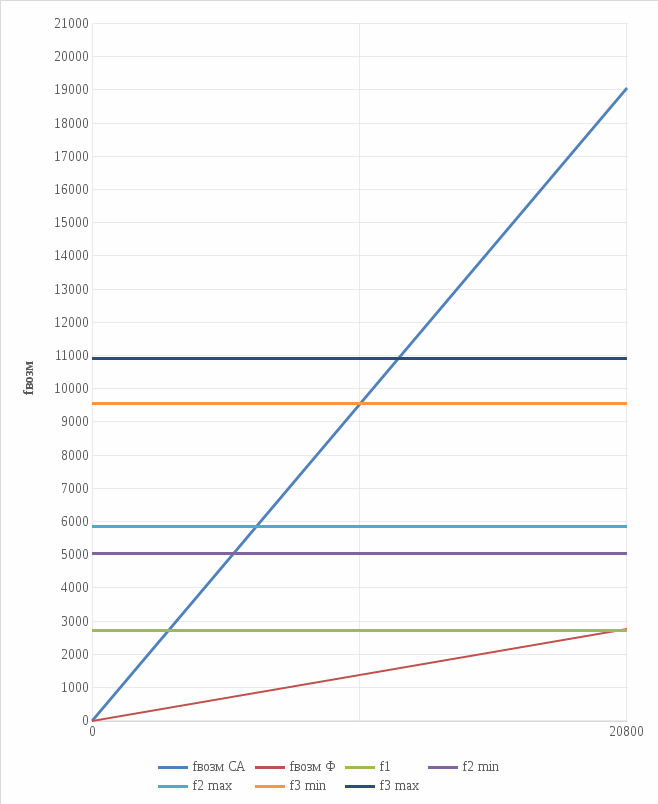
Рисунок 6 – Частотная диаграмма
Из анализа частотной диаграммы можно сделать вывод о том, что лопатка первой ступени турбины не соответствует требованиям динамической прочности, так как возмущающая сила, вызванная наличием форсунок создаёт резонансную точку на рабочем диапазоне частот, пересекаясь с частотой первой формы собственных колебаний лопатки на частоте порядка 20500 Гц.
Способом вывода резонансных режимов работы за пределы рабочего диапазона частот вращения ротора можно считать уменьшение числа форсунок до 7, что сместит резонансную точку за границу рабочих режимов.
При запуске и останове двигателя будет наблюдаться резонанс от возмущающей силы сопловых аппаратов, но он не критичен так как происходит за границей рабочего диапазона.
Решение дифференциального уравнения простейшей колебательной системы
В случае свободных колебаний уравнение, описывающее движение простейшей колебательной системы с одной степенью свободы (рисунок А.1) можно записать в следующем виде:
m · a + k · x = 0,
(А.1)
где: a – ускорение точечной массы m (произведение m·a представляет силу инерции, действующую на массу m);
k · x – произведение, представляющее силу упругости, с которой упругий стержень действует на массу m.
Рисунок А.1 – Простейшая колебательная система с одной степенью свободы
В соответствии со схемой системы (рисунок 1) и режимом колебаний никакие другие силы на стержень и массу m не действуют, поэтому в левой части уравнения (А.1) слагаемых больше нет, а правая его часть равна нулю.
Поскольку ускорение свободного конца стержня a равно второй производной от его координаты x по времени t, уравнение (А.1) может быть представлено в следующем виде:
Разделив левую и правую части уравнения (А.2) на массу m, получим:
Уравнение (А.3), которое представляет собой обыкновенное(содержащее один аргумент – t), линейное(в уравнении присутствуют искомая функция x(t) и ее производные только в первой степени), однородное(правая часть уравнения равна нулю) дифференциальноеуравнение, может быть решено с помощью подстановки x(t) = eλ·t. Выполнив эту подстановку и взяв вторую производную в первом слагаемом левой части уравнения (3), получим:
Разделив левую и правую части уравнения (А.4) на eλ·t и обозначив k/m = ω2, придем к так называемому характеристическомууравнению:
Характеристическое уравнение (А.5) является алгебраическим, из него может быть найден параметр λ:
где: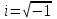
- мнимая единица.
В соответствии с теорией обыкновенных дифференциальных уравнений общим решением исходного дифференциального уравнения (А.3) будет следующее выражение:
где: С1 и С2 - постоянные числа (в общем случае – комплексные), которые могут быть определены по заданным начальным условиям;
eiωt и e-iωt - частные решения уравнения (А.3).
Выберем в качестве начальных условий момент начала свободных колебаний, когда при t = 0 после мгновенного приложения возмущающей силы свободный конец упругого стержня занял положение, соответствующее координате x0, при этом dx(t)/dt = 0. В этом случае, учитывая, что e0 = 1, из уравнения (А.7) получим:
Из равенства (А.8) видно, что сумма коэффициентов С1 и С2 (являющихся в общем случае комплексными числами) равна действительному числу x0: C1 + C2 = x0 . Такое равенство может быть справедливым в двух случаях:
- когда С1 и С2 являются действительными числами;
- когда С1 и С2 - комплексно сопряженные числа вида:
Тогда:
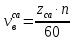– частота возмущающей силы, вызванной наличием сопловых аппаратов, 1/с; 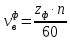– частота возмущающей силы, вызванной наличием форсунок, 1/с; 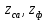– число лопаток соплового аппарата первой ступени турбины и число форсунок в камере сгорания;n – частота вращения ротора, об/мин.
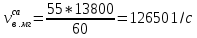
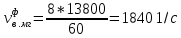
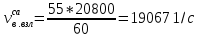
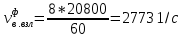
Линии изменения частот возмущающей силы и частот собственных колебаний наносятся на график в координатах
.В случае близости резонансных точек к границам рабочего диапазона оборотов ротора двигателя определяется запас по частоте вращения.
Если в рабочем диапазоне частот вращения ротора окажутся резонансные точки, то делается вывод о том, что рабочая лопатка не удовлетворяет требованиям динамической прочности.
Линии изменения частот возмущающей силы и частот собственных колебаний наносятся на график (рис.6) в координатах
.В случае близости резонансных точек к границам рабочего диапазона оборотов ротора двигателя определяется запас по частоте вращения.
Если в рабочем диапазоне частот вращения ротора окажутся резонансные точки, то делается вывод о том, что рабочая лопатка не удовлетворяет требованиям динамической прочности.
об/мин
Рисунок 6 – Частотная диаграмма
3.3 Вывод
Из анализа частотной диаграммы можно сделать вывод о том, что лопатка первой ступени турбины не соответствует требованиям динамической прочности, так как возмущающая сила, вызванная наличием форсунок создаёт резонансную точку на рабочем диапазоне частот, пересекаясь с частотой первой формы собственных колебаний лопатки на частоте порядка 20500 Гц.
Способом вывода резонансных режимов работы за пределы рабочего диапазона частот вращения ротора можно считать уменьшение числа форсунок до 7, что сместит резонансную точку за границу рабочих режимов.
При запуске и останове двигателя будет наблюдаться резонанс от возмущающей силы сопловых аппаратов, но он не критичен так как происходит за границей рабочего диапазона.
Список использованных источников
-
Макаров Н.В., Шерлыгин Н.А. Авиационные газотурбинные двигатели. Прочность и конструкция: Учебное пособие. – Л.: ОЛАГА, 1976. – 96 С. -
Устройство и летная эксплуатация силовых установок: Учебное пособие для вузов/ Соловьев Б.А., Куландин А.А., Макаров Н.В. и др. – М.: Транспорт, 1991. – 256 С. -
Конструкция и прочность авиационных газотурбинных двигателей/ Лозицкий Л.П. и др. – М.: Воздушный транспорт, 1992. – 536 С. -
Прочность и динамика узлов авиационных газотурбинных двигателей: /Конспект лекций, под ред. Умушкина Б.П./ – М.: МГТУ ГА, 1994. – 104 С. -
Макаров, Н.В. Конструкция и эксплуатация авиационных двигателей, воздушных судов и авиационные материалы [Текст]: Методические указания к выполнению I части курсового проекта «Авиационные двигатели» / Н.В. Макаров. – Л.: ОЛАГА, 1990. – 48 С. -
Богданов, А.Д. Авиационный турбовинтовой двигатель ТВ2-117 [Текст]: Учебное пособие для авиац.-техн. училищ гражд. авиации / А. Д. Богданов, И. Г. Хаустов. – М.: Транспорт, 1970. – 371 С. -
Иноземцев, А. А. Основы конструирования авиационных двигателей и энергетических установок [Текст]: учебник для студентов высших учебных заведений / А. А. Иноземцев, М. А. Нахамкин, В. Л. Сандрацкий. – М.: Машиностроение, 2008. – 207 С. -
Кулагин В.В. Теория, расчет и проектирование авиационных двигателей и энергетических установок: Учебник. 2-е изд. Кн. 1. Основы теории ГТД рабочий процесс и термогазодинамический анализ. Кн. 2. Совместная работа узлов выполненного двигателя и его характеристики.- М.: Машиностроение, 2003. – 616 С. -
Руководство по технической эксплуатации ТВ2-117
Приложение А
Решение дифференциального уравнения простейшей колебательной системы
В случае свободных колебаний уравнение, описывающее движение простейшей колебательной системы с одной степенью свободы (рисунок А.1) можно записать в следующем виде:
m · a + k · x = 0,
(А.1)где: a – ускорение точечной массы m (произведение m·a представляет силу инерции, действующую на массу m);
k · x – произведение, представляющее силу упругости, с которой упругий стержень действует на массу m.
Рисунок А.1 – Простейшая колебательная система с одной степенью свободы
В соответствии со схемой системы (рисунок 1) и режимом колебаний никакие другие силы на стержень и массу m не действуют, поэтому в левой части уравнения (А.1) слагаемых больше нет, а правая его часть равна нулю.
Поскольку ускорение свободного конца стержня a равно второй производной от его координаты x по времени t, уравнение (А.1) может быть представлено в следующем виде:
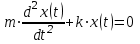| |  | (А.2) |
Разделив левую и правую части уравнения (А.2) на массу m, получим:
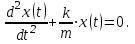| |  | (А.3) |
Уравнение (А.3), которое представляет собой обыкновенное(содержащее один аргумент – t), линейное(в уравнении присутствуют искомая функция x(t) и ее производные только в первой степени), однородное(правая часть уравнения равна нулю) дифференциальноеуравнение, может быть решено с помощью подстановки x(t) = eλ·t. Выполнив эту подстановку и взяв вторую производную в первом слагаемом левой части уравнения (3), получим:
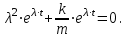| |  | (А.4) |
Разделив левую и правую части уравнения (А.4) на eλ·t и обозначив k/m = ω2, придем к так называемому характеристическомууравнению:
| | λ2 + ω2 = 0. | (А.5) |
Характеристическое уравнение (А.5) является алгебраическим, из него может быть найден параметр λ:
| | λ2 = - ω2; 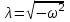 ;  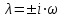, | (А.6) |
где:
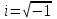- мнимая единица.В соответствии с теорией обыкновенных дифференциальных уравнений общим решением исходного дифференциального уравнения (А.3) будет следующее выражение:
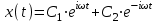| |  , | (А.7) |
где: С1 и С2 - постоянные числа (в общем случае – комплексные), которые могут быть определены по заданным начальным условиям;
eiωt и e-iωt - частные решения уравнения (А.3).
Выберем в качестве начальных условий момент начала свободных колебаний, когда при t = 0 после мгновенного приложения возмущающей силы свободный конец упругого стержня занял положение, соответствующее координате x0, при этом dx(t)/dt = 0. В этом случае, учитывая, что e0 = 1, из уравнения (А.7) получим:
| | x(0) = x0 = C1 + C2 . | (А.8) |
Из равенства (А.8) видно, что сумма коэффициентов С1 и С2 (являющихся в общем случае комплексными числами) равна действительному числу x0: C1 + C2 = x0 . Такое равенство может быть справедливым в двух случаях:
- когда С1 и С2 являются действительными числами;
- когда С1 и С2 - комплексно сопряженные числа вида: