ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 63
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования РФ
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Уфимский университет науки и технологий»
Факультет информатики и робототехники
Кафедра вычислительной математики и кибернетики
Расчетно-графическая работа
«Имитация СМО с одним устройством»
по дисциплине
«Компьютерное моделирование»
Выполнил:
студент группы ПРО-328
Ямалтдинова А. А.
Проверила:
Валеева А. Ф.
Уфа 2023
Оглавление
Постановка задачи 2
Пояснения к модели 2
Оценки модели 3
Описание модели 4
Анализ модели 9
Верификация имитационной модели 10
Вывод 10
1. Написать имитационный алгоритм и программу.
2. Выполнить верификацию имитационной программы.
3. Провести анализ очереди из клиентов в течение интервала времени [0, T].
Во всех моделях СМО предполагается, что клиенты прибывают согласно неоднородному Пуассоновскому процессу с ограниченной функцией интенсивности
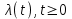 .
.Постановка задачи
Имеется парикмахерская с одним устройством, куда пребывают клиенты. График с 8 до 20, в среднем в час поступает 3 клиента.
Допущения:
-
Клиенты пребывают в систему, имеющую одно устройство и одну очередь. -
Когда клиенты поступают в систему, если устройство занято, то они образуют очередь, иначе поступают на устройство. -
Когда обслуживание клиента заканчивается, он покидает систему и клиент, который дольше всех находится в очереди, начинает обслуживаться.
Пояснения к модели
-
Устройство обслуживания – робот-парикмахер -
Требование – клиенты -
Единица времени – час -
Интенсивность – 3 человека в час -
Функция интенсивности –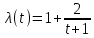
-
Время работы T – 12 часов (с 8 до 20)
Обеденный перерыв отсутствует, есть вероятность переработки (последний клиент уйдет после закрытия магазина).
Оценки модели
-
Оценка ожидаемой средней задержки клиентов в очереди:
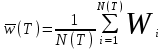 ,
,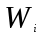 — время задержки клиента iв очереди,
— время задержки клиента iв очереди, 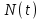 - число клиентов, которые прибыли в период времени
- число клиентов, которые прибыли в период времени 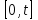
-
Оценку ожидаемого среднего числа клиентов в очереди:
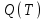 - число клиентов в системе в период времени
- число клиентов в системе в период времени 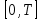 .
. 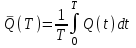
-
Оценка занятости устройства – ожидаемый коэффициент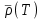 использования устройства (время, когда устройство занято/период моделированияT), где функция занятости В(t):
использования устройства (время, когда устройство занято/период моделированияT), где функция занятости В(t):
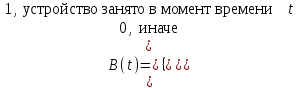
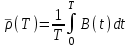
-
Среднее время, в течение которого клиент проводит в системе, вычисляется как:
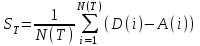 ,
, где
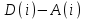 - это количество времени, в течение которого клиент
- это количество времени, в течение которого клиент 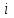 проводит в системе;
проводит в системе; 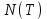 - общее число клиентов, которые пришли до времени
- общее число клиентов, которые пришли до времени 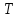 .
.-
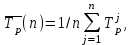
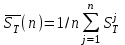 (оценки для математических ожиданий
(оценки для математических ожиданий 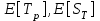 , имитация проводится
, имитация проводится 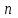 раз,
раз, 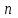 - достаточно велико).
- достаточно велико).
Описание модели
Вспомогательные функции
-
Функция интенсивности
Входные данные:
t – время в системе.
Выходные данные:
Значение функции интенсивности в момент времени t.
Функция интенсивности: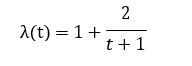
-
Функция генерации неоднородного пуассоновского процесса
Входные данные:
s – время в системе
L – интенсивность появления событий
Выходные данные:
t – время следующего события в системе
Алгоритм (poisson(t, lambd)):
-
Присвоить t = s -
Генерируем случайную переменную U1 = Uniform[0, 1] -
Присвоить t =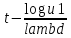
-
Генерируем случайную переменную U2 = Uniform[0, 1], независимую от U1. -
Если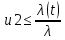 , то:
, то:-
Ts = t -
Конец алгоритма
-
-
Иначе повторить с шага 2.
-
Функция генерации случайной величины
Входные данные:
L – интенсивность появления событий
Выходные данные:
Y – значение показателей случайной величины
Алгоритм (exponentional(lambd)):
-
Генерируем случайное число U = Uniform[0, 1] -
Возвращаем величину Y =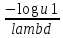
Реализация алгоритма. Процедуры работы СМО.
Переменная времени:
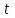
Количественные переменные:
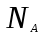 - число прибывших клиентов к моменту времени
- число прибывших клиентов к моменту времени 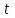
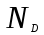 - число уходов клиентов к моменту времени
- число уходов клиентов к моменту времени 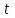
Переменная состояния:
 - число клиентов в системе к моменту времени
- число клиентов в системе к моменту времени 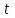
События: пребывания и уходы клиентов.
Список событий:
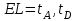
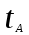 - время следующего прибытия клиента (после
- время следующего прибытия клиента (после 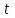 );
); 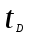 - время завершения работы устройства после обслуживания клиента
- время завершения работы устройства после обслуживания клиента (
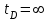 если никакой клиент в данный момент не обслужен).
если никакой клиент в данный момент не обслужен).Случайные переменные:
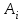 — время поступления клиента
— время поступления клиента  ;
; 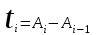
— время между поступлениями клиентов i - 1 и
 (t0= 0);
(t0= 0); 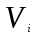 — время, потраченное устройством на обслуживание клиентаi
— время, потраченное устройством на обслуживание клиентаi (без учета времени задержки клиента в очереди);
 — время задержки клиента iв очереди;
— время задержки клиента iв очереди;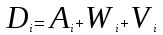 — время ухода клиента iпо завершении
— время ухода клиента iпо завершении обслуживания;
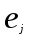 — время возникновения события j любого типа.
— время возникновения события j любого типа. Выходные переменные:
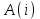 - время прибытия клиента
- время прибытия клиента 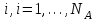
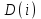 - время ухода клиента
- время ухода клиента 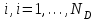
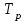 - время после
- время после  , когда последний клиент уходит
, когда последний клиент уходит - количество времени, в течение которого клиент
- количество времени, в течение которого клиент  проводит в системе
проводит в системе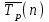 - оценка среднего времени после
- оценка среднего времени после  , когда уходит последний клиент
, когда уходит последний клиент 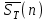 - оценка среднего времени, в течение которого клиент проводит в системе
- оценка среднего времени, в течение которого клиент проводит в системе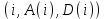 ,
, 
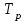 - наблюдаемое значение (время после
- наблюдаемое значение (время после  , когда ушел последний клиент)
, когда ушел последний клиент) - число клиентов в системе в период времени
- число клиентов в системе в период времени 
Amount – количество клиентов за смену
Tp – время задержки закрытия
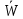 – среднее время клиентов в очереди
– среднее время клиентов в очереди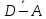 – среднее время клиента в системе
– среднее время клиента в системе1-Work/T – коэффициент занятости устройства
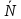 – средняя длина очереди
– средняя длина очереди События:
-
прибытие клиента -
уход клиента -
клиент ушел – но очередь не пуста -
клиент ушел – и время работы закончилось
Общая схема алгоритма имитации СМО с одним устройством:
Пусть
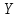 - случайная переменная – время обслуживания устройства с распределением
- случайная переменная – время обслуживания устройства с распределением 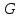 .
.Инициализация переменных
Присвоить
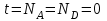
Присвоить
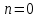
Генерировать
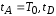 =
=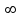
Изменения системы будут происходить в зависимости от того, какое событие будет следующим – прибытие или уход клиента, при этом рассматриваются различные случаи.
Случай 1 – прибытие клиента(tA
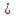 tD, tA
tD, tA 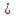 T)
T)Алгоритм:
-
Присвоить t = tA (движение вдоль оси времени ко времени tA) -
Присвоить NA = NA+1 (подсчитано более одного прибытия к моменту времени tA) -
Присвоить n = n+1 (в настоящее время имеется более одного клиента) -
Запустить функцию генерации неоднородного пуассоновского процесса (poisson(t, lambd)) и присвоить полученное значение tA (время следующего прибытия клиента) -
Если n = 1, генерировать случайную переменную Y(exponentional(lambd)) имеющую показательное распределение и присвоить tD= t+ Y(exponentional(lambd)) -
Запомнить выходные данные A(NA) = t (время прибытия клиента NA)