Файл: Отчет По расчётнографической работе По дисциплине Основы теории управления.docx

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Новосибирский государственный технический университет»

Кафедра вычислительной техники

Отчет

По расчётно-графической работе

По дисциплине: «Основы теории управления»

Выполнил: Преподаватель: Воевода А.А.

Группа:

Новосибирск, 2022

Цель работы

Исследовать систему, состоящую из трёх пружин и трёх грузов. Провести теоретические расчёты и реализовать систему в пакете Matlab Simulink. Добиться устойчивости системы путём расчёта и добавления к ней регулятора. Перевести получившуюся систему в дискретный вид.

Задание

Дана трёхмассовая система без демпфирования (d1=d2=d3=0):





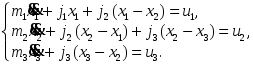
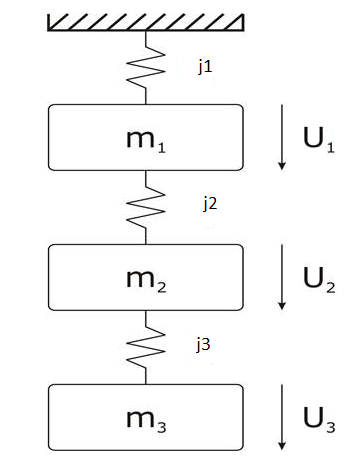
Рис.1. Схема задания

Сила прикладывается только ко второй массе u1=u3=0. Стоит задача управлять положением первой массы x1. В качестве входных параметров были взяты: m1 = 3, m2 = 2, m3 = 1, j1 = 4, j2 = 5, j3 = 6. В качестве входного сигнала – u2.

Ход работы

Силы, действующие на данную систему систему:







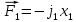
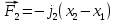
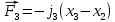
Составим систему на основе второго закона Ньютона:



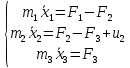
Тогда



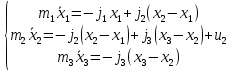
Преобразование Лапаласа:



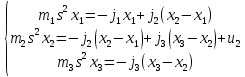
Выразим:



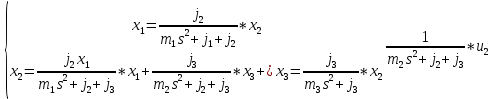
Найдём решение системы в Matchad:



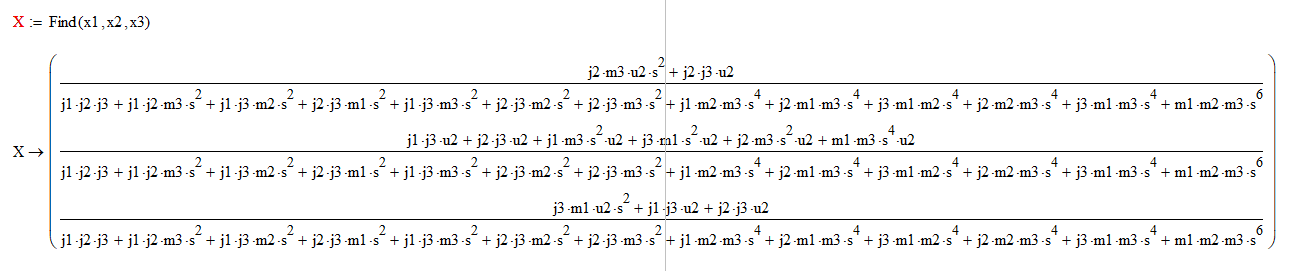
Нас интересует

---

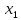
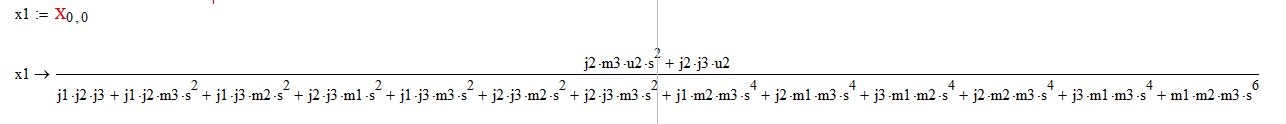
Теперь необходимо подставить исходные значения в полученный полином.



Тогда передаточная функция системы будет иметь вид:



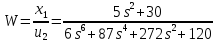
Схема в Simulik:



Рис.2. Построенная схема в Simulink



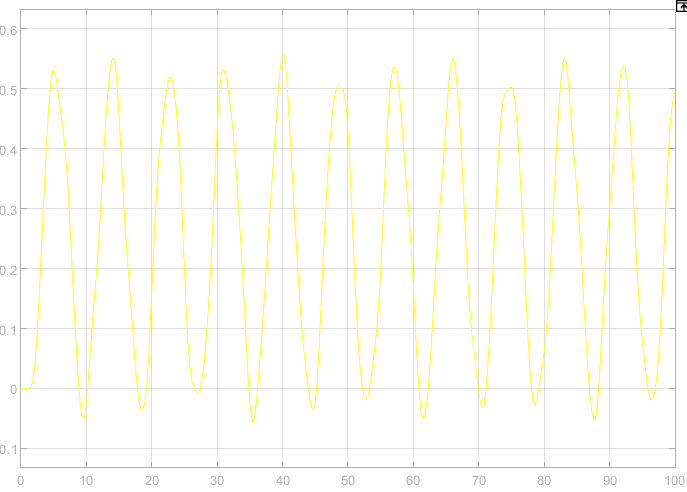
Рис.3.График переходной функции системы

С помощью Simulink построим диаграмму Боде и годограф Найквиста:





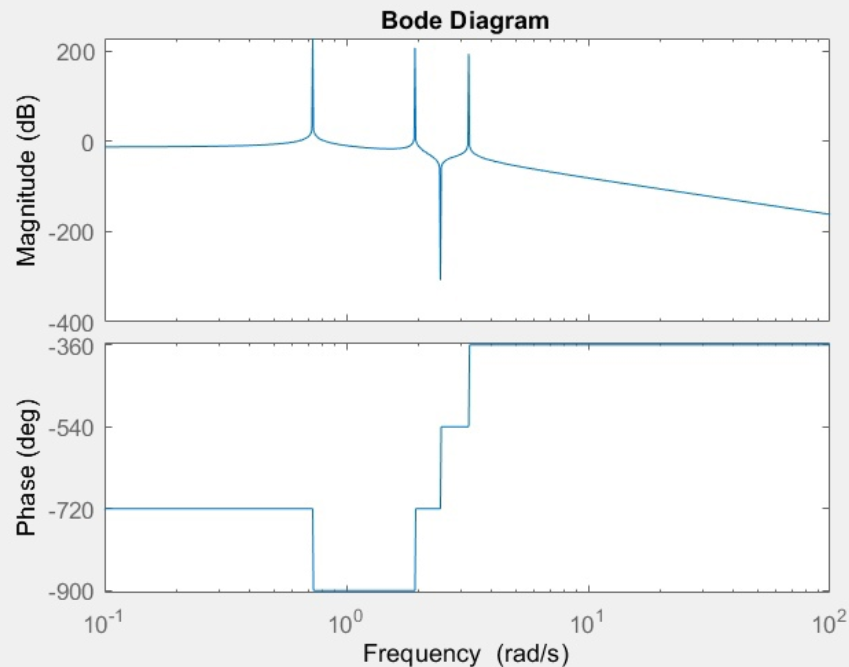
Рис.4. ЛАЧХ и ЛФЧХ



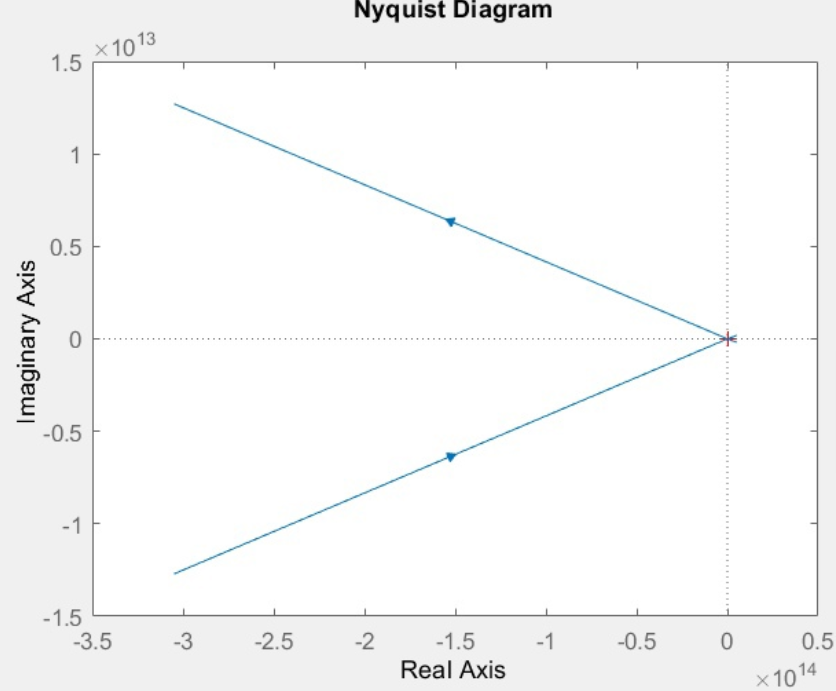
Рис.5. Годограф Найквиста

Найдём корни ХПЗС в Matlab:



Рис.7. Поиск корней

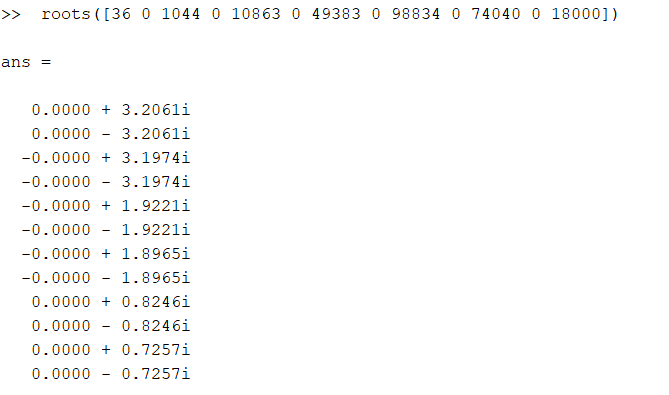
Рис.6. Корни ХПЗС

Как видно из рис.8 система находится на границе устойчивости

По методу размещения полюсов передаточной функции замкнутой системы выберем регулятор. Проведем необходимые вычисления в система MatchCAD. Приходим к тому, что ХПЗС сводится к биному Ньютона 11 степени. Тогда останется приравнять коэффициенты при одинаковых степенях s – решить матричное уравнение.



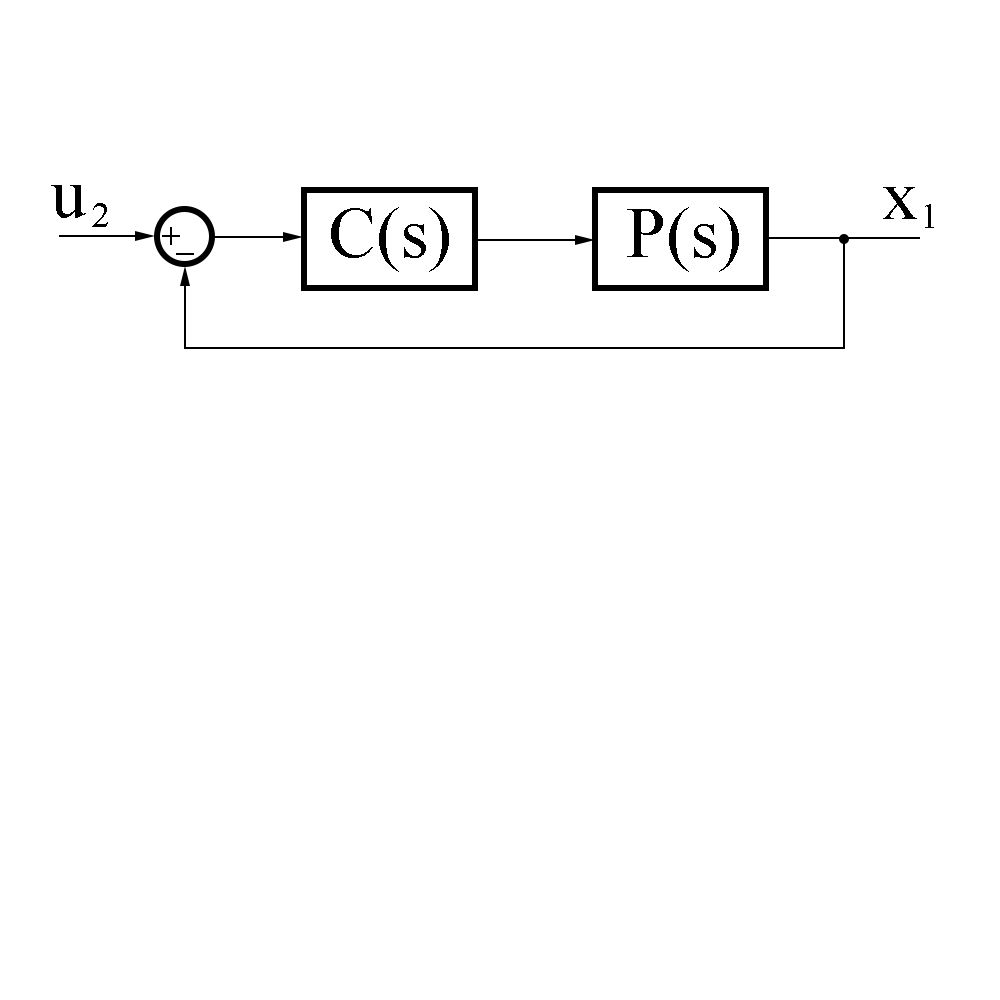
Рисунок 7. Структурная схема системы с регулятором в общем виде

Где 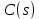– регулятор, 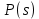– объект управления.

Выберем регулятор вида:





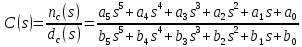
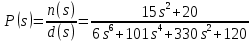
Необходимо определить коэффициенты

---

, .

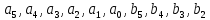
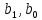ХПЗС:




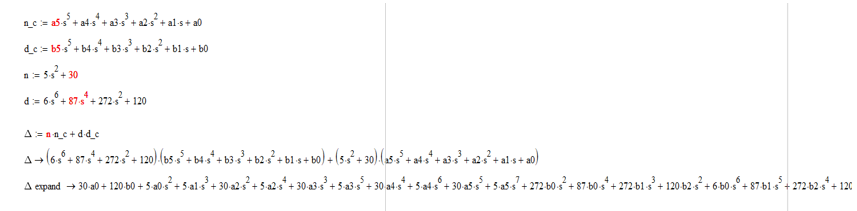
Предположим, что мы хотим выбрать регулятор так, чтобы разместить корни полинома 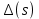в заданных точках, то есть добиться выполнения равенства .

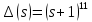По биному Ньютона:



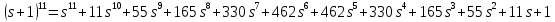
Поиск неизвестных коэффициентов сводим к решению матричного уравнения вида:

,

,

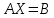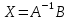где X – искомые коэффициенты, A – коэффициенты при X, B – коэффициенты бинома Ньютона.





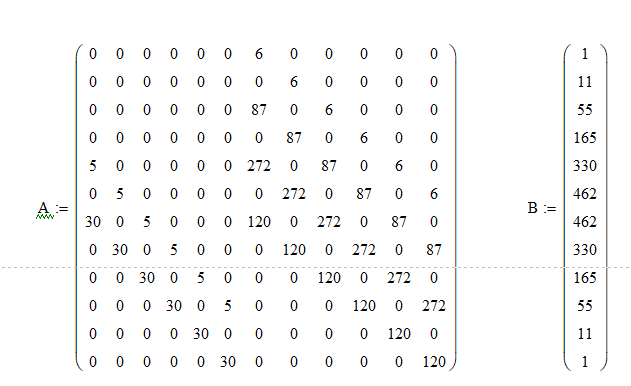
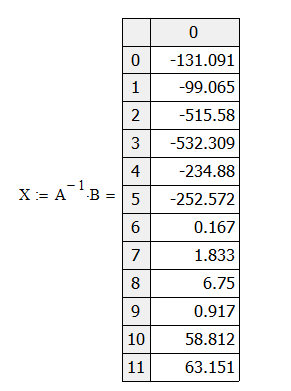
Рис.7. Найденные коэффициенты регулятора
Подставим полученные коэффициенты в регулятора и соберем структурную схему в Simulink:



Рис.8. Структурная схема с регулятором



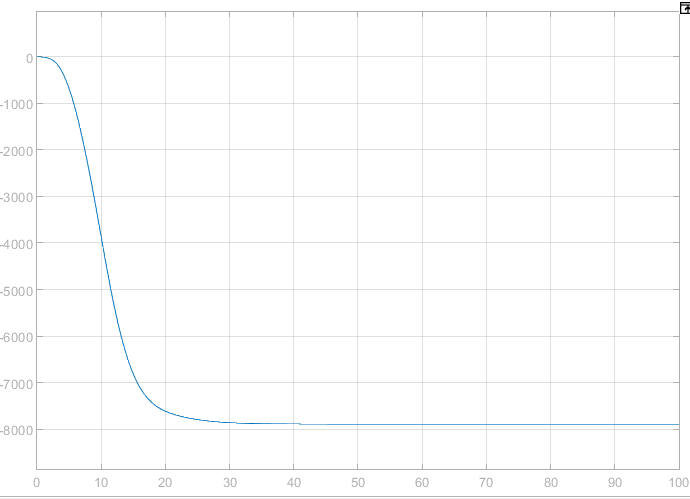
Рис.9. График переходной функции

Построим в Matlab диаграммы bode и годограф Найкфиста:










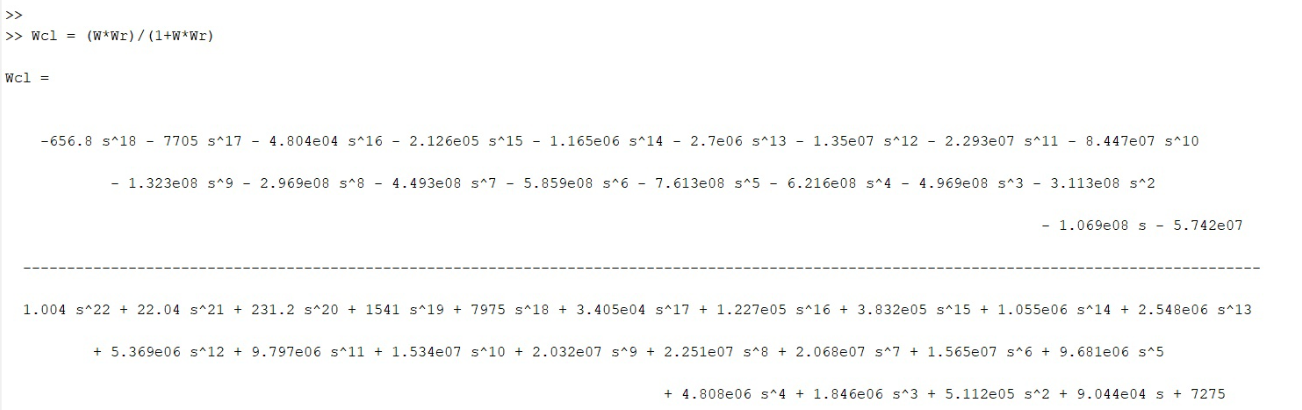
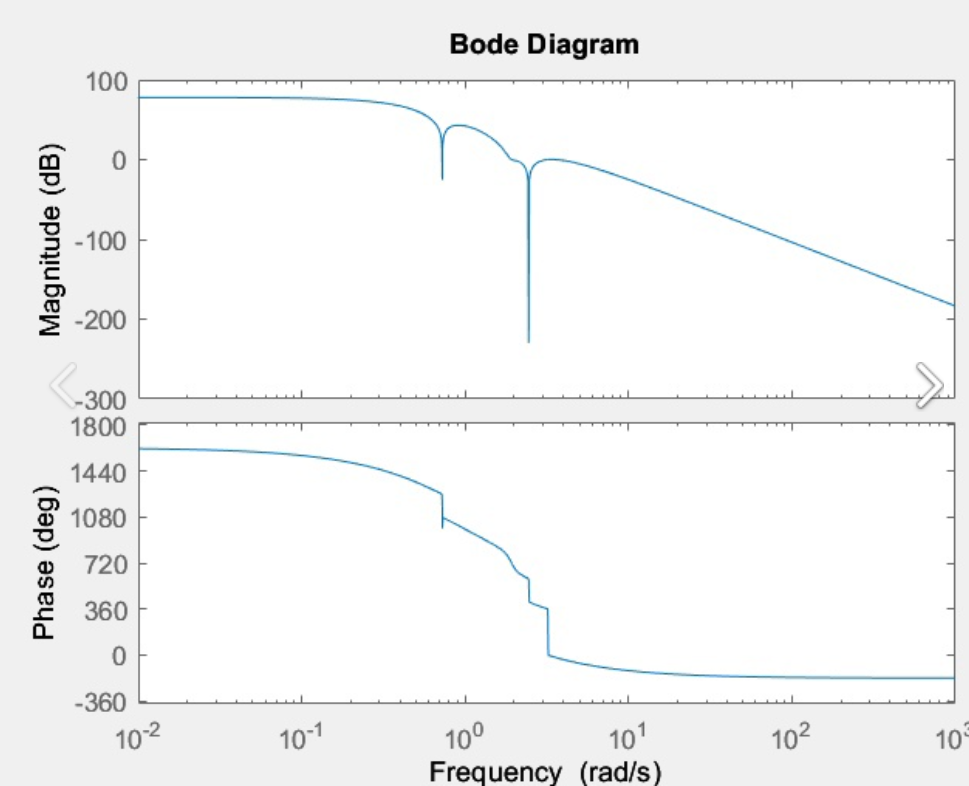
Рис.10 ЛАЧХ и ЛФЧХ



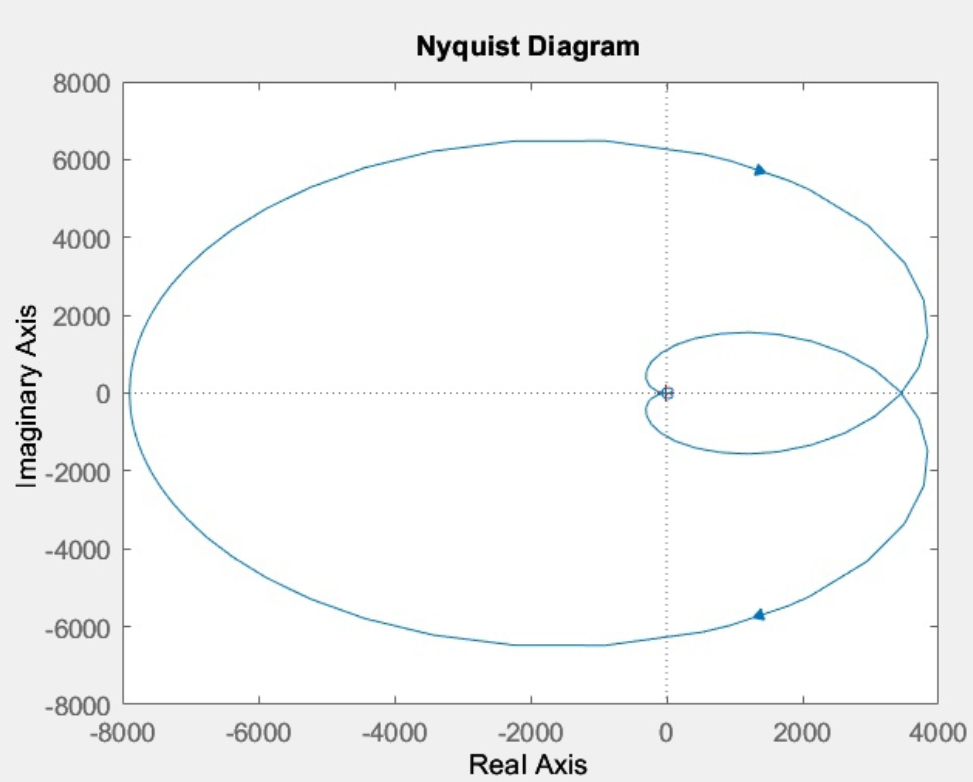
Рис.11 Годограф Найквиста

---

Рис.12. Корни ХПЗС

Так как все корни ХПЗС расположены в левой полуплоскоти, то система устойчива.

Переведем теперь систему в дискретный вид, используя функцию c2d(), transfer function регулятора и шаг дискретизации 0.1.



Теперь соберём схему в Simulink, заменив блок Trunsfer func у регулятора на блок Discrete Trunsfer func:



Рис.13. Структурная схема с дискретным регулятором



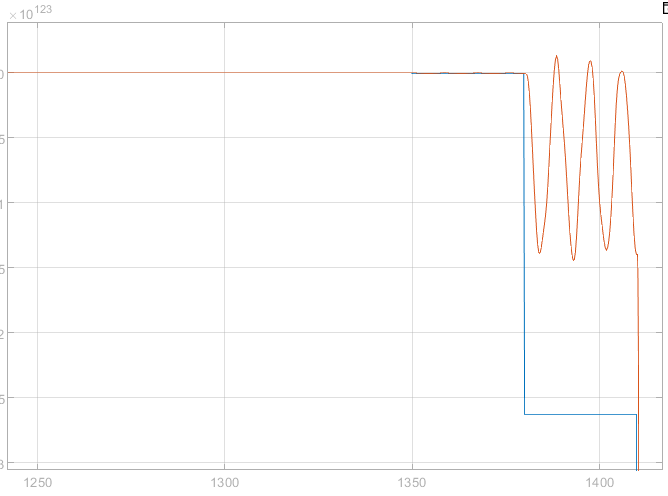
Рис.14. График

Вывод

В ходе выполнения работы была исследована система из трех пружин и трех грузов. Найдена transfer function зависимости входного и выходного сигналов. Найден регулятор для достижения устойчивости системы, он же переведен в дискретный вид.

---