Файл: Курсовая работа Ишкова Мария Андреевна Преподаватель Григорьева Елена Игоревна Воронеж 2021 Оглавление.docx
Добавлен: 10.01.2024
Просмотров: 94
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНОБРНАУКИ РОССИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Математический факультет
«Методы решений систем линейных уравнений в MS Excel»
Курсовая работа
Выполнила:
Ишкова Мария Андреевна
Преподаватель:
Григорьева Елена Игоревна
Воронеж 2021
Оглавление
Введение 2
Системы линейных алгебраических уравнений (СЛАУ) и методы их решения в MS Excel. 4
Системы линейных алгебраических уравнений и их значение. 4
Решение системы с помощью матричного метода 6
Решение системы с помощью метода Крамера 8
Примеры решения СЛАУ в MS Excel 10
Матричный метод: 10
Метод Крамера: 12
Заключение 16
Список литературы 17
Введение
В бытовых ситуациях мы очень часто сталкиваемся с математическими расчетами, не говоря уже об профессиональной или учебной деятельности, где решение задач является обязательным. Будь то простые арифметические действия или основы алгебры логики.
Однако, для профессиональных вопросов возникает необходимость в решении систем линейных уравнений. Например, при конструировании сооружений, анализе результатов измерений и ряда других задач техники, экономики, физики.
Проблема численного решения систем линейных уравнений интересует математиков не одно столетие, даже в веке технического прогресс тема не потеряла своей актуальности.
С появлением первых ЭВМ были активные попытки увеличить точность существовавших способов. Вплоть до 80-х годов решение вычислительных задач было ограничено техническими возможностями, поэтому особое значение придавалось экономичности алгоритмов. Интерес к «задачам с неизвестным» с новыми методами решений, нестандартными подходами и применением современных технологий только возрос.
Поиск нужного ответа привычным способом на бумаге может занимать большое количество времени и сил. Мало кто знает, что компьютерные программы могут не только сократить время, но и свести к минимуму участие человека в решении задачи.
Примером такой программы служит MS Excel. О ее широких возможностях и помощи в поиске «х» может не знать даже продвинутый пользователь. Главное преимущество Office Excel – это наличие огромного количества встроенных стандартных функций, что позволяет легко и быстро делать различные вычисления. Вышесказанное определило актуальность моей темы и позволило определить цель и сформулировать задачи работы.
Объект исследования: возможности MS Excel.
Цель работы: исследовать возможные методы решения систем линейных уравнений в программе MS Excel.
Для достижения цели мной были поставлены следующие задачи исследования:
-
Собрать и проанализировать информацию по теме. -
Изучить возможные и известные методы решения. -
Применить полученные знания на практических примерах.
Практическая значимость моей работы заключается в систематизации знаний по данной теме, в использовании различных источников, поиска наиболее оптимального варианта решений задач темы.
Системы линейных алгебраических уравнений (СЛАУ) и методы их решения в MS Excel.
Системы линейных алгебраических уравнений и их значение.
Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Фигурная скобка означает, что все уравнения должны выполняться одновременно.
Решить систему уравнений - это значит найти все её решения или установить, что их нет. Из школьного курса алгебры нам известно три способа решения уравнений:
-
Графический. Чтобы уравнений решить систему графическим способом нужно построить графики уравнений, входящих в систему, на одной координатной плоскости и найти точки их пересечения. -
Сложение. Чтобы решить систему двух линейных уравнений с двумя переменными методом сложения необходимо следовать алгоритму: сначала уравнять модули коэффициентов при одном из неизвестных (если необходимо), затем сложить или вычесть уравнения. -
Подстановка. Чтобы решить систему уравнений методом подстановки необходимо: в одном из уравнений выразить одну переменную через другую, подставить полученное выражение во второе уравнение системы, решить полученное уравнение с одной неизвестной, найти значение второй переменной.
На уроках отрабатываются навыки решения систем линейных уравнений этими способами. Системы линейных алгебраических уравнений широко используются в инженерных расчетах, в том числе по химической технологии и защите окружающей среды.
Но в обычной жизни мы чаще сталкиваемся с задачами, в которых нужно найти три или более неизвестных. В этом случае решение системы 3-мя перечисленными методами достаточно времязатратный и трудоемкий процесс, поэтому для упрощения поиска выгоднее воспользоваться компьютерной программой (в моем случае MS Excel).
Системы трех и более уравнений приходится решать другими способами.
К ним относятся:
-
Метод обратной матрицы -
Метод Крамера
В дальнейшей работе разберу их подробнее.
Решение системы с помощью матричного метода
Метод обратной матрицы - метод, который используется при решении систем уравнений в том случае, если число неизвестных равняется числу уравнений. Для того чтобы найти корни уравнения этим способом, в первую очередь находят обратную матрицу, которую перемножают на свободные коэффициенты.
Шаги решения в MS Excel:
-
Возьмем систему уравнений. -
Запишем свободные коэффициенты системы уравнений в следующем виде. -
Скопируем матрицу коэффициентов и таблицу свободных коэффициентов. -
Теперь нужно создать обратную матрицу. Для этого выделяем ячейки в которых будет новая матрица, далее в строке формул нужно задать «=МОБР» и указать массив матрицы, для которой мы создаем обратную матрицу. После этого нажать комбинацию клавиш «Ctrl+Shift+Enter». -
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной. -
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
=МУМНОЖ(Массив1;Массив2)
-
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию». -
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK». -
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. -
Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. -
После данного действия в предварительно выделенной ячейке отобразятся корни уравнения: X1, X2, X3 и X4. Они будут расположены последовательно. Таким образом, можно сказать, что мы решили данную систему. -
Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.
Решение системы с помощью метода Крамера
Метод Крамера часто применяется для систем линейных алгебраических уравнений (СЛАУ). Этот способ решения считается одним из самых простых. Ног есть условие, что данный метод применяется только для тех систем, где по количеству неизвестных столько же, сколько и уравнений. Чтобы получилось решить уравнение, главный определитель матрицы не должен равняться нулю.
Шаги решения в MS Excel:
-
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно». -
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. -
Теперь необходимо вычислить определители всех таблиц. С помощью функции «=МОПРЕД». Выделяем ячейку, в которой будет выводиться определитель первой матрицы. -
Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию». Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK». -
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. -
После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш «Ctrl+Shift+Enter». -
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. -
Аналогичным образом производим подсчет определителей для остальных трех таблиц. -
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит система уравнений имеет решения. -
Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число, которое является определителем первоначальной таблицы, мы получим четыре корня. Они и являются ответом.
Эти способы решения СЛАУ достаточно понятны и доступны. Но, когда я выполняла практическую часть и решала системы уравнений сама, я заметила, что матричный метод намного легче в применении.
Примеры решения СЛАУ в MS Excel
В практической части своей работы я хочу подробнее описать каждый из приведенных методов, на примере уравнения для каждого способа. В качестве проверки решения, в конце сравню получившиеся корни. Так как для примера взято одно уравнение, они должны быть равными.
Матричный метод:
-
Решим систему уравнений:
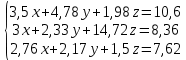
-
Выпишем отдельно «x=;y=;z=;», чтобы потом сразу показать полученные значения:
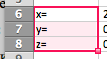
-
Запишем все численные коэффициенты уравнения в таблицу:
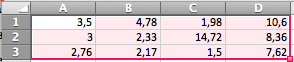
-
Суть матричного метода заключается в формуле: X=A-1B. Для сокращения количества действий, можно сразу задать сложную формулу. Первые 3 столбца – матрица А, та для которой нужно найти обратную, а последний столбец – матрица В, столбец свободных членов. Эти две матрицы необходимо перемножить. -
Затем выбираем диапазон из 3-х ячеек:

-
Записываем формулу:

где формула «=мумнож» - это функция для умножения матриц, так как нам нужна матрица обратная матрице А, используем функцию «=мобр», указываем диапазоны и нажимаем комбинацию клавиш «Ctrl+Shift+Enter».
-
Получаем искомые значения:
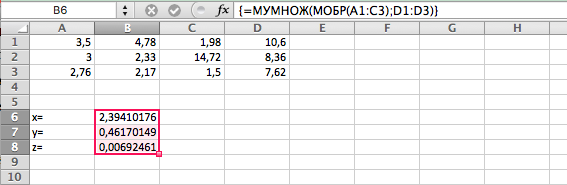
Метод Крамера:
-
Решим систему уравнений:
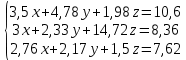
-
Запишем все численные коэффициенты уравнения в таблицу:
-
Пусть в диапазоне А6:С8, будут главный определитель, а в диапазоне А10:С12 будет определитель, полученный из главного заменой столбцом свободных членов коэффициентов при х: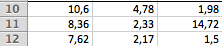
-
Во второй части заменяем столбцом свободных членов столбец с значениями второй переменной: