Файл: Методические указания по выполнению расчётнографической работы и организации самостоятельной работы содержание.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 310
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
ОБЩИЕ ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮРАСЧЁТНО-ГРАФИЧЕСКОЙ РАБОТЫ
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЗАДАНИЯ №2
ПО ТЕМЕ «ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЗАДАНИЯ №3
ПО ТЕМЕ «ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
ПО ТЕМЕ «ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
ПО ТЕМЕ «ПАРНАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ»
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯЗАДАНИЯ №5
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЩИТЕЗАДАНИЯ №5
ПО ТЕМЕ «ТРЕНД-СЕЗОННЫЕ МОДЕЛИ ВРЕМЕННЫХ РЯДОВ»
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯЗАДАНИЯ №6
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЗАДАНИЯ №4
ПО ТЕМЕ «ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
(КРИТЕРИЙ ПИРСОНА)»
Задание 4. В таблице приведены результаты исследования возраста у 100 случайно выбранных работников государственных предприятий N-й области.
| Возраст, лет | 15-25 | 25-35 | 35-45 | 45-55 | 55-65 | Итого |
| Число рабочих, чел. | 6 | 24 | 37 | 22 | 11 | 100 |
При уровне значимости 0,05 проверить гипотезу о нормальном распределении возраста работников государственных предприятий N-й области.
Решение.
Определим средний возраст работников и выборочную дисперсию, взяв середину интервала в качестве xi.
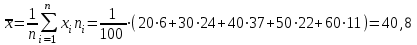
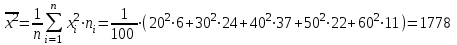
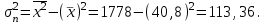
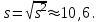
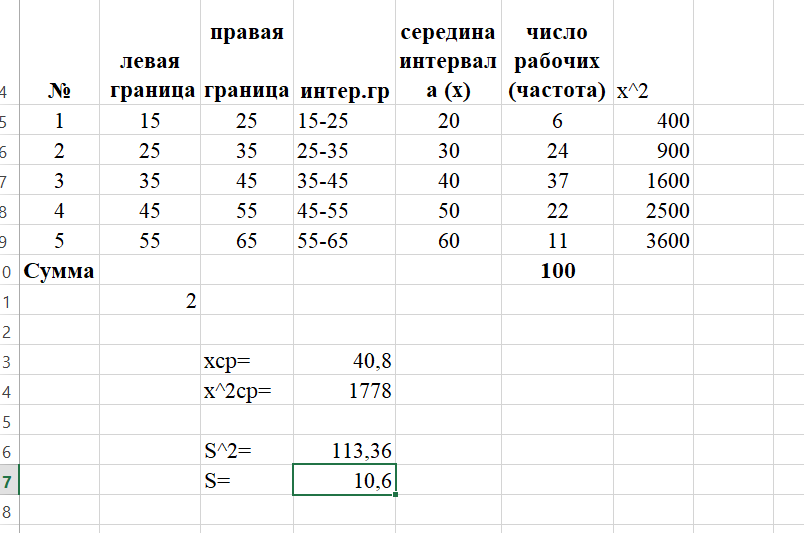
Выдвинем гипотезу Н0: возраст работников предприятий подчиняется нормальному распределению с параметрами
 40,8 и s10,6 и конкурирующую гипотезу Н1: возраст работников предприятий не подчиняется нормальному распределению. Для проверки гипотезы воспользуемся критерием Пирсона.
40,8 и s10,6 и конкурирующую гипотезу Н1: возраст работников предприятий не подчиняется нормальному распределению. Для проверки гипотезы воспользуемся критерием Пирсона.Так как для всех интервалов частоты ni 5, то нет необходимости в объединении интервалов. Расширим первый и последний интервалы так, чтобы закрыть все множество действительных чисел, т.е. левую границу первого интервала положим равной , а правую границу последнего интервала . Полученные интервалы запишем в таблицу, в которой также рассчитаны вероятности
pi (вычисления приводятся под таблицей 10) и теоретические частоты niT.
Таблица 10
Расчетная таблица
| I | 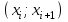 | ni | pi | niT=npi | 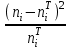 | |
| 1 | (; 25) | 6 | 0,0681 | 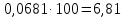 | 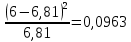 | |
| 2 | (25; 35) | 24 | 0,2231 | 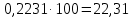 | 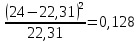 | |
| 3 | (35; 45) | 37 | 0,3642 | 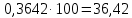 | 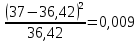 | |
| 4 | (45; 55) | 22 | 0,2545 | 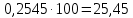 | 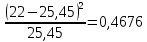 | |
| 5 | (55; ) | 11 | 0,0901 | 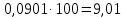 | 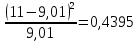 | |
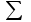 | 100 | 1 | 100 | 1,1404 | ||
Таким образом, наблюдаемое значение критерия
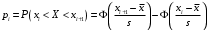 .
.Значения функции Ф(х) выбираются из таблицы приложения 1.
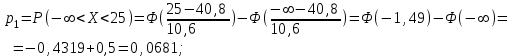
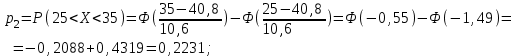
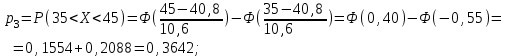
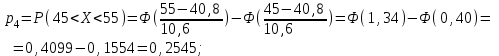
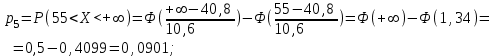
Таким образом, наблюдаемое значение критерия:
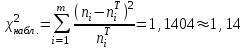
Для определения значения χ2кр(;k) вычислим число степеней свободы k m 3 53 2. По таблице критического распределенияχ2 (приложение 2)находим критическую точку χ2кр(0,05; 2) = 5,9916,0.
Так как χ2набл. <χ2кр, то гипотеза о нормальном распределении возраста работников государственных предприятий принимается.
ЗАДАНИЕ №4 ПО ВАРИАНТАМ
Задание 4. В таблице приведены результаты исследования возраста у 100 случайно выбранных работников государственных предприятий N-й области. При уровне значимости 0,05 проверить гипотезу о нормальном распределении возраста работников государственных предприятий N-й области
Вариант 1
| Возраст, лет | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | Итого |
| Число рабочих, чел. | 17 | 23 | 8 | 32 | 20 | 100 |
Вариант 2
| Возраст, лет | 15-25 | 25-35 | 35-45 | 45-55 | 55-65 | Итого |
| Число рабочих, чел. | 14 | 16 | 27 | 33 | 10 | 100 |
Вариант 3
| Возраст, лет | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | Итого |
| Число рабочих, чел. | 14 | 16 | 27 | 33 | 10 | 100 |
Вариант 4
| Возраст, лет | 18-28 | 28-38 | 38-48 | 48-58 | 58-68 | Итого |
| Число рабочих, чел. | 10 | 24 | 27 | 22 | 17 | 100 |
Вариант 5
| Возраст, лет | 15-22 | 22-29 | 29-36 | 36-43 | 43-50 | Итого |
| Число рабочих, чел. | 20 | 24 | 23 | 11 | 22 | 100 |
Вариант 6
| Возраст, лет | 22-32 | 32-42 | 42-52 | 52-62 | 62-72 | Итого |
| Число рабочих, чел. | 10 | 20 | 30 | 29 | 11 | 100 |
Вариант 7
| Возраст, лет | 15-20 | 20-25 | 25-30 | 30-35 | 35-40 | Итого |
| Число рабочих, чел. | 7 | 31 | 30 | 22 | 10 | 100 |