Файл: Методические указания по выполнению расчётнографической работы и организации самостоятельной работы содержание.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 309
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
ОБЩИЕ ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮРАСЧЁТНО-ГРАФИЧЕСКОЙ РАБОТЫ
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЗАДАНИЯ №2
ПО ТЕМЕ «ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯ ЗАДАНИЯ №3
ПО ТЕМЕ «ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
ПО ТЕМЕ «ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
ПО ТЕМЕ «ПАРНАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ»
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯЗАДАНИЯ №5
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЗАЩИТЕЗАДАНИЯ №5
ПО ТЕМЕ «ТРЕНД-СЕЗОННЫЕ МОДЕЛИ ВРЕМЕННЫХ РЯДОВ»
ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯЗАДАНИЯ №6
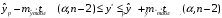 ,
,a) для среднего прогнозного значения:
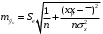 ,
,б) для индивидуального прогнозного значения:
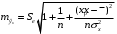 .
.ПОЯСНЕНИЯ И ОБРАЗЕЦ ВЫПОЛНЕНИЯ
ЗАДАНИЯ №5
Исходные данные:
Известны следующие поквартальные данные по торговой фирме за последние 16 кварталов.
| Объем продаж(y), тыс. руб. | Расходы на рекламу, тыс. руб. | Цена товара, руб. | Цена конкурента, руб. |
| 126 | 4 | 15 | 17 |
| 137 | 4,8 | 14,8 | 17,3 |
| 148 | 3,8 | 15,2 | 16,8 |
| 191 | 8,7 | 15,5 | 16,2 |
| 274 | 8,2 | 15,5 | 16 |
| 370 | 9,7 | 16 | 18 |
| 432 | 14,7 | 18,1 | 20,2 |
| 445 | 18,7 | 13 | 15,8 |
| 367 | 19,8 | 15,8 | 18,2 |
| 367 | 10,6 | 16,9 | 16,8 |
| 321 | 8,6 | 16,3 | 17 |
| 307 | 6,5 | 16,1 | 18,3 |
| 331 | 12,6 | 15,4 | 16,4 |
| 345 | 6,5 | 15,7 | 16,2 |
| 364 | 5,8 | 16 | 17,7 |
| 384 | 5,7 | 15,1 | 16,2 |
Задания:
1. Построить уравнение парной линейной регрессии yна х, где Объем продаж (y) – зависимая переменная, а в качестве независимой переменной х необходимо выбрать один фактор из нескольких предложенных, имеющий наибольшую взаимосвязь с зависимой переменной. Выбор данного фактора необходимо осуществить на основании сравнения величин линейных коэффициентов корреляции.
-
Сформировать расчетную таблицу заданной структуры.
№
x
y
xy
x2

e
e2



1










n
Сумма
Среднее
-
Ввести ряды данных в таблицу по столбцам. Рассчитать суммы и средние рядов данных с помощью функций СУММ(…) и СРЗНАЧ(…). -
Построить корреляционное поле при помощи Мастера диаграмм (тип – Точечная диаграмма) и провести визуальный анализ. -
Рассчитать параметры линейного выборочного уравнения парной регрессии с использованием формул:
с использованием формул:

-
Найти значения выборочных дисперсий и СКО x, y по формулам:


Проверить результат с помощью функций:
ДИСПР(…) и СТАНДОТКЛОНП(…).
-
Рассчитать выборочный коэффициент корреляции с использованием одной из формул:
 .
.Проверить результат с помощью функции КОРРЕЛ(…).
-
Вычислить средний коэффициент эластичности .
. -
Вычислить предсказанные моделью значения y по построенному уравнению регрессии .
. -
Вычислить остатки и их квадраты. Остатки вычисляются по формуле .
. -
Вычислить значения ,
,  .
. -
Рассчитать суммы квадратов отклонений (СумКО), дисперсии и СКО на 1 степень свободы (общая, факторная, остаточная).
 ,
,  ,
,  ,
, ,
,  ,
,  ,
,где TSS – общая СумКО (total sum of squares), ESS – факторная СумКО , RSS – остаточная СумКО.
-
Проверить балансовое соотношение для суммы квадратов отклонений:
 .
.
-
Рассчитать коэффициент детерминации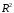 и индекс корреляции с
и индекс корреляции с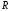 использование сумм квадратов отклонений:
использование сумм квадратов отклонений:
 ,
,  .
.Проверить результат с использованием коэффициента корреляции

и с помощью функции КВПИРСОН(…).
-
Рассчитать стандартную ошибку коэффициента регрессии и значение статистики Стьюдента:
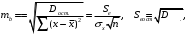
 .
.-
Проверить статистическую значимость коэффициента b на уровнях 0,05 и 0,01. При определении табличного значения статистики воспользоваться функцией СТЬЮДРАСПОБР(…). Если |tb|>tтабл(α;n-2), то коэффициент b статистически значимо отличен от нуля. -
Построить доверительный интервал для коэффициента регрессии на уровне значимости 0,01:
 .
.-
Рассчитать значение статистики Фишера F через факторную и остаточную дисперсии: .
. -
Проверить результат вычисления статистики с использованием коэффициента детерминации и статистики Стьюдента для b:
 ,
, 
-
Проверить статистическую значимость уравнения в целом на уровне 0,05. Табличное значение F определить через функцию
FРАСПОБР(…). Если , то уравнение признается в целом статистически значимым.
, то уравнение признается в целом статистически значимым. -
Проверить качество уравнения по средней относительной ошибки аппроксимации:

-
С помощью инструмента Регрессия Пакета анализа построить линейную регрессию y на x. Найти , если прогнозное значение фактора увеличится на 5% от его среднего значения.
, если прогнозное значение фактора увеличится на 5% от его среднего значения. -
Подставить прогноз в уравнение регрессии y на x и получить прогноз
в уравнение регрессии y на x и получить прогноз  .
. -
Построить 95% -й интервал прогноза :
:
 ,
,a) для среднего прогнозного значения:
 ,
,б) для индивидуального прогнозного значения:
