ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 87
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2. Кинематический и силовой расчёт привода.
2.2 Передаточные отношения привода и отдельных его передач.
2.3 Частоты вращения, угловые скорости, мощности и моменты на валах привода.
3 Расчёт косозубой передачи редуктора.
3.1 Материалы зубчатых колёс и допускаемые напряжения.
Для стальных колёс с твердостью менее НВ 350 /2, с.34/ / Учебник Чернавский С.А. :
3.2 Расчёт геометрических параметров косозубой передачи.
,
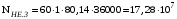 .
.
Без вычислений по формуле (3.3) видно, что коэффициент долговечности для каждого из колёс окажется меньше единицы, так как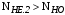 и
и 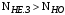 .
.
В таком случае следует принимать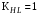 /2, с.33/.
/2, с.33/.
Если взять коэффициент безопасности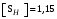 (для улучшенной стали) /2, с.33/, то расчёт по формулам (3.1) и (3.2) даст допускаемые контактные напряжения для шестерни и колеса соответственно
(для улучшенной стали) /2, с.33/, то расчёт по формулам (3.1) и (3.2) даст допускаемые контактные напряжения для шестерни и колеса соответственно
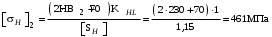 ,
,
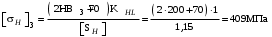 .
.
В частном случае для косозубых передач допускаемое контактное напряжение при расчёте на выносливость /2, с.35/
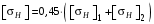 , (3.5)
, (3.5)
при соблюдении условия
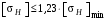 , где
, где 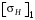 и
и  – соответственно допускаемые контактные напряжения для шестерни и колеса, вычисленные по формуле (3.1), МПа;
– соответственно допускаемые контактные напряжения для шестерни и колеса, вычисленные по формуле (3.1), МПа;
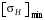 – меньшее из двух напряжений, входящих в правую часть формулы (3.5), МПа.
– меньшее из двух напряжений, входящих в правую часть формулы (3.5), МПа.
Расчёт по формуле (3.5) даёт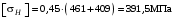 .
.
Условие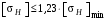 выполняется, так как
выполняется, так как 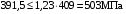 .
.
3.1.3 Допускаемое контактное напряжение при кратковременных перегрузках для колёс из улучшенной стали зависит от предела текучести и вычисляется по формуле /3, с.187/:
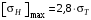 , (3.6)
, (3.6)
При σТ = 400 МПа (минимальное значение для колеса по пункту 3.1.1)
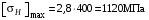 .
.
3.1.4 Допускаемые напряжения изгиба при проверочном расчёте зубьев на выносливость вычисляются по формуле /3, с.190/:
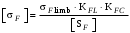 , (3.7)
, (3.7)
где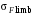 – предел выносливости материала зубьев при отнулевом цикле, соответствующий базовому числу циклов, МПа;
– предел выносливости материала зубьев при отнулевом цикле, соответствующий базовому числу циклов, МПа; 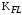
– коэффициент долговечности при расчёте зубьев на изгиб;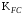 – коэффициент, учитывающий влияние двустороннего приложения нагрузки на зубья (в случае реверсивной передачи);
– коэффициент, учитывающий влияние двустороннего приложения нагрузки на зубья (в случае реверсивной передачи); 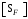 – допускаемый коэффициент безопасности (запаса прочности).
– допускаемый коэффициент безопасности (запаса прочности).
По рекомендации /2, с.43…45/ берём:
– для улучшенных сталей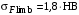 ; – при одностороннем нагружении зубьев, принимая привод нереверсивным
; – при одностороннем нагружении зубьев, принимая привод нереверсивным 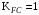 ; – для стальных поковок и штамповок при твёрдости менее НВ 350
; – для стальных поковок и штамповок при твёрдости менее НВ 350 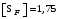 .
.
Коэффициент долговечности /3, с.191/
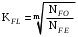 , (3.8)
, (3.8)
где m – показатель корня;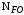 – базовое число циклов;
– базовое число циклов;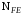 – эквивалентное (действительное) число циклов перемены напряжений.
– эквивалентное (действительное) число циклов перемены напряжений.
Для колёс с твёрдостью зубьев до и более НВ 350 величина m равна соответственно 6 и 9. Для всех сталей принимается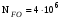 .
.
Для обоих колёс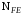 имеет те же численные значения, что и
имеет те же численные значения, что и  (см. пункт 3.1.2). Оба эти значения (для шестерни – 86,4·107, для колеса – 17,28·107) больше
(см. пункт 3.1.2). Оба эти значения (для шестерни – 86,4·107, для колеса – 17,28·107) больше 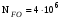 .
.
Поэтому, принимается коэффициент долговечности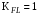 /3, с.191, 921/.
/3, с.191, 921/.
Расчёт по формуле (3.7) даёт соответственно для шестерни и колеса
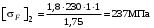 ,
, 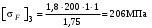 .
.
3.1.5 Допускаемое напряжение изгиба при расчёте зубьев на кратковременные перегрузки при твёрдости менее НВ 350 /2, с.193/
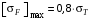 , (3.9)
, (3.9)
Расчёт по этой формуле с учётом характеристик материала (см. 3.1.1) даёт для шестерни и колеса соответственно
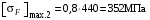 ,
, 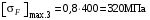
.
Межосевое расстояние цилиндрической зубчатой передачи из условия контактной выносливости активных поверхностей зубьев /2, с.32/
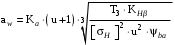 , (3.10)
, (3.10)
где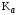 – коэффициент, равный 43 для косозубых колёс; u – передаточное число зубчатой пары; Т3 – момент на колесе (на большем из колёс), Н·м;
– коэффициент, равный 43 для косозубых колёс; u – передаточное число зубчатой пары; Т3 – момент на колесе (на большем из колёс), Н·м;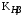 – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца;
– коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца; 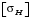 – допускаемое контактное напряжение, МПа;
– допускаемое контактное напряжение, МПа; 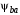 – коэффициент ширины венца по межосевому расстоянию.
– коэффициент ширины венца по межосевому расстоянию.
Передаточное число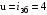 , а момент Т3 = 739,85 Н·м (см. раздел 2). Допускаемое напряжение
, а момент Т3 = 739,85 Н·м (см. раздел 2). Допускаемое напряжение 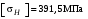 вычислено в пункте 3.1.2.
вычислено в пункте 3.1.2.
Коэффициент ширины венца по межосевому расстоянию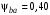 возьмём по рекомендации /2, с.33/ для косозубых передач. При несимметричном расположении колёс относительно опор принимаем ориентировочно
возьмём по рекомендации /2, с.33/ для косозубых передач. При несимметричном расположении колёс относительно опор принимаем ориентировочно 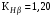 /2, с.32/.В итоге расчёт по формуле (3.10) даёт
/2, с.32/.В итоге расчёт по формуле (3.10) даёт 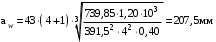
.
Межосевое расстояние округляем до стандартного значения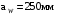 /2, с.36/.
/2, с.36/.
Нормальный модуль /2, с.36/
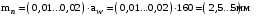 .
.
Из стандартного ряда модулей /2, с.36/ берём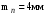 .
.
Назначим предварительно угол наклона линии зуба для косозубых колёс β = 10° /2, с.37/.
Тогда, суммарное число зубьев
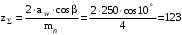 .
.
Определяем число зубьев шестерни: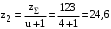
Принимаем z2 = 24, тогда число зубьев колеса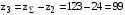 .
.
Фактическое передаточное отношение
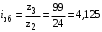 .
.
Расхождение с принятым ранее номинальным передаточным отношением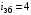 составляет
составляет 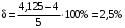 , что допустимо (не превышает 3%).
, что допустимо (не превышает 3%).
Уточнённое значение
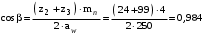
соответствует β = 10,2631° = 10°15'47"
Кинематическая схема исследуемого редуктора приведена на рисунке 3.1
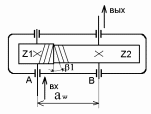
Рис. 3.1. Кинематическая схема одноступенчатого цилиндрического редуктора с косозубой передачей.
Косозубые цилиндрические передачи целесообразно проверять на выполнение условия /2, с.36/
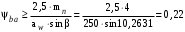 .
.
При принятом значении коэффициента ширины венца по межосевому расстоянию условие выполняется.
условие выполняется.
При обработке шестерни с числом зубьев z2 = 24 подрезание зубьев исключается, так как условие неподрезания /2, с.38/
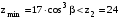
соблюдено, что видно и без расчёта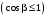 .
.
Делительные диаметры шестерни и колеса соответственно
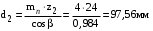 ,
, 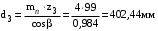 .
.
Правильность вычислений подтверждается проверкой
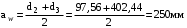 , что верно.
, что верно.
Диаметры вершин зубьев
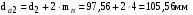 ,
,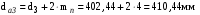 .
.
Диаметры впадин зубьев
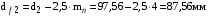 ,
,
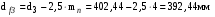 .
.
Ширина колеса
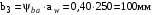 .
.
Ширина шестерни
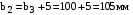 .
.
Коэффициент ширины шестерни по диаметру
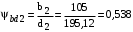 .
.
3.3.1 Расчётное контактное напряжение для косозубых цилиндрических передач /2, с.31/
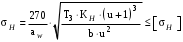 , (3.11)
, (3.11)
где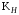
– коэффициент нагрузки; b – ширина колеса расчётная (наименьшая).
Остальные символы в формуле расшифрованы ранее.
Окружная скорость колёс
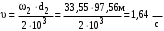 .
.
При такой скорости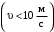 назначаем восьмую степень точности /2, с.32/.
назначаем восьмую степень точности /2, с.32/.
Коэффициент нагрузки /2, с.32/ при проверочном расчёте на контактную прочность
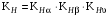 , (3.12)
, (3.12)
где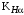 – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями;
– коэффициент, учитывающий неравномерность распределения нагрузки между зубьями; 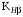 – коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба (по ширине венца);
– коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба (по ширине венца);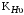 – коэффициент, учитывающий дополнительные динамические нагрузки (динамический коэффициент).
– коэффициент, учитывающий дополнительные динамические нагрузки (динамический коэффициент).
По рекомендациям /2, с.39, 40/ назначаем следующие значения перечисленных коэффициентов: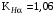 при окружной скорости
при окружной скорости 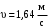 и восьмой степени точности;
и восьмой степени точности; 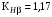 при значении коэффициента
при значении коэффициента 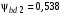 , твёрдости зубьев менее НВ 350 и несимметричном расположении колёс относительно опор;
, твёрдости зубьев менее НВ 350 и несимметричном расположении колёс относительно опор; 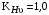 при окружной скорости
при окружной скорости 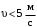 , восьмой степени точности и твёрдости менее НВ 350.
, восьмой степени точности и твёрдости менее НВ 350.
Расчёт по формуле (3.1) даёт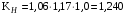 .
.
Ширину колеса берём в расчёт минимальную b = 100 мм. Момент на колесе Т3 = 739,85 Н·м.
Расчёт по формуле (3.11) даёт
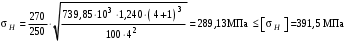 .
.
Условие прочности выполняется. Недогрузка составляет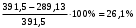 . Она объясняется увеличением первоначально вычисленного межосевого расстояния до стандартного
. Она объясняется увеличением первоначально вычисленного межосевого расстояния до стандартного  .
.
3.3.2 Расчёт зубьев на контактную прочность по формуле (3.11) при кратковременных перегрузках моментом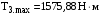 (см. раздел 2) даёт
(см. раздел 2) даёт
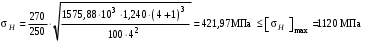
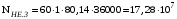 .
.Без вычислений по формуле (3.3) видно, что коэффициент долговечности для каждого из колёс окажется меньше единицы, так как
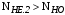 и
и 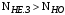 .
.В таком случае следует принимать
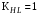 /2, с.33/.
/2, с.33/.Если взять коэффициент безопасности
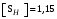 (для улучшенной стали) /2, с.33/, то расчёт по формулам (3.1) и (3.2) даст допускаемые контактные напряжения для шестерни и колеса соответственно
(для улучшенной стали) /2, с.33/, то расчёт по формулам (3.1) и (3.2) даст допускаемые контактные напряжения для шестерни и колеса соответственно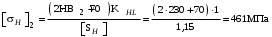 ,
,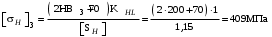 .
.В частном случае для косозубых передач допускаемое контактное напряжение при расчёте на выносливость /2, с.35/
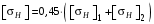 , (3.5)
, (3.5)при соблюдении условия
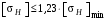 , где
, где 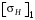 и
и  – соответственно допускаемые контактные напряжения для шестерни и колеса, вычисленные по формуле (3.1), МПа;
– соответственно допускаемые контактные напряжения для шестерни и колеса, вычисленные по формуле (3.1), МПа;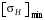 – меньшее из двух напряжений, входящих в правую часть формулы (3.5), МПа.
– меньшее из двух напряжений, входящих в правую часть формулы (3.5), МПа.Расчёт по формуле (3.5) даёт
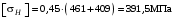 .
.Условие
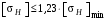 выполняется, так как
выполняется, так как 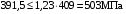 .
.3.1.3 Допускаемое контактное напряжение при кратковременных перегрузках для колёс из улучшенной стали зависит от предела текучести и вычисляется по формуле /3, с.187/:
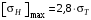 , (3.6)
, (3.6)При σТ = 400 МПа (минимальное значение для колеса по пункту 3.1.1)
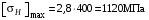 .
.3.1.4 Допускаемые напряжения изгиба при проверочном расчёте зубьев на выносливость вычисляются по формуле /3, с.190/:
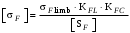 , (3.7)
, (3.7)где
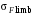 – предел выносливости материала зубьев при отнулевом цикле, соответствующий базовому числу циклов, МПа;
– предел выносливости материала зубьев при отнулевом цикле, соответствующий базовому числу циклов, МПа; 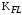
– коэффициент долговечности при расчёте зубьев на изгиб;
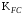 – коэффициент, учитывающий влияние двустороннего приложения нагрузки на зубья (в случае реверсивной передачи);
– коэффициент, учитывающий влияние двустороннего приложения нагрузки на зубья (в случае реверсивной передачи); 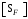 – допускаемый коэффициент безопасности (запаса прочности).
– допускаемый коэффициент безопасности (запаса прочности).По рекомендации /2, с.43…45/ берём:
– для улучшенных сталей
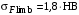 ; – при одностороннем нагружении зубьев, принимая привод нереверсивным
; – при одностороннем нагружении зубьев, принимая привод нереверсивным 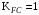 ; – для стальных поковок и штамповок при твёрдости менее НВ 350
; – для стальных поковок и штамповок при твёрдости менее НВ 350 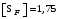 .
.Коэффициент долговечности /3, с.191/
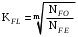 , (3.8)
, (3.8)где m – показатель корня;
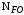 – базовое число циклов;
– базовое число циклов;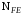 – эквивалентное (действительное) число циклов перемены напряжений.
– эквивалентное (действительное) число циклов перемены напряжений.Для колёс с твёрдостью зубьев до и более НВ 350 величина m равна соответственно 6 и 9. Для всех сталей принимается
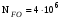 .
.Для обоих колёс
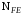 имеет те же численные значения, что и
имеет те же численные значения, что и  (см. пункт 3.1.2). Оба эти значения (для шестерни – 86,4·107, для колеса – 17,28·107) больше
(см. пункт 3.1.2). Оба эти значения (для шестерни – 86,4·107, для колеса – 17,28·107) больше 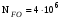 .
.Поэтому, принимается коэффициент долговечности
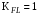 /3, с.191, 921/.
/3, с.191, 921/.Расчёт по формуле (3.7) даёт соответственно для шестерни и колеса
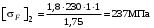 ,
, 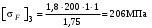 .
.3.1.5 Допускаемое напряжение изгиба при расчёте зубьев на кратковременные перегрузки при твёрдости менее НВ 350 /2, с.193/
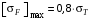 , (3.9)
, (3.9)Расчёт по этой формуле с учётом характеристик материала (см. 3.1.1) даёт для шестерни и колеса соответственно
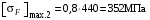 ,
, 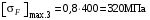
.
3.2 Расчёт геометрических параметров косозубой передачи.
Межосевое расстояние цилиндрической зубчатой передачи из условия контактной выносливости активных поверхностей зубьев /2, с.32/
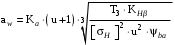 , (3.10)
, (3.10)где
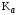 – коэффициент, равный 43 для косозубых колёс; u – передаточное число зубчатой пары; Т3 – момент на колесе (на большем из колёс), Н·м;
– коэффициент, равный 43 для косозубых колёс; u – передаточное число зубчатой пары; Т3 – момент на колесе (на большем из колёс), Н·м;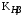 – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца;
– коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца; 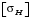 – допускаемое контактное напряжение, МПа;
– допускаемое контактное напряжение, МПа; 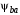 – коэффициент ширины венца по межосевому расстоянию.
– коэффициент ширины венца по межосевому расстоянию.Передаточное число
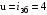 , а момент Т3 = 739,85 Н·м (см. раздел 2). Допускаемое напряжение
, а момент Т3 = 739,85 Н·м (см. раздел 2). Допускаемое напряжение 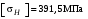 вычислено в пункте 3.1.2.
вычислено в пункте 3.1.2.Коэффициент ширины венца по межосевому расстоянию
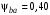 возьмём по рекомендации /2, с.33/ для косозубых передач. При несимметричном расположении колёс относительно опор принимаем ориентировочно
возьмём по рекомендации /2, с.33/ для косозубых передач. При несимметричном расположении колёс относительно опор принимаем ориентировочно 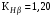 /2, с.32/.В итоге расчёт по формуле (3.10) даёт
/2, с.32/.В итоге расчёт по формуле (3.10) даёт 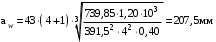
.
Межосевое расстояние округляем до стандартного значения
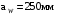 /2, с.36/.
/2, с.36/.Нормальный модуль /2, с.36/
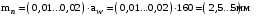 .
.Из стандартного ряда модулей /2, с.36/ берём
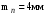 .
.Назначим предварительно угол наклона линии зуба для косозубых колёс β = 10° /2, с.37/.
Тогда, суммарное число зубьев
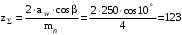 .
.Определяем число зубьев шестерни:
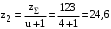
Принимаем z2 = 24, тогда число зубьев колеса
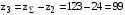 .
.Фактическое передаточное отношение
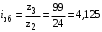 .
.Расхождение с принятым ранее номинальным передаточным отношением
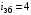 составляет
составляет 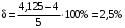 , что допустимо (не превышает 3%).
, что допустимо (не превышает 3%).Уточнённое значение
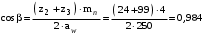
соответствует β = 10,2631° = 10°15'47"
Кинематическая схема исследуемого редуктора приведена на рисунке 3.1

Рис. 3.1. Кинематическая схема одноступенчатого цилиндрического редуктора с косозубой передачей.
Косозубые цилиндрические передачи целесообразно проверять на выполнение условия /2, с.36/
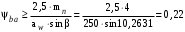 .
.При принятом значении коэффициента ширины венца по межосевому расстоянию
 условие выполняется.
условие выполняется.При обработке шестерни с числом зубьев z2 = 24 подрезание зубьев исключается, так как условие неподрезания /2, с.38/
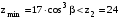
соблюдено, что видно и без расчёта
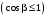 .
.Делительные диаметры шестерни и колеса соответственно
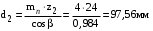 ,
, 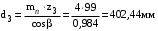 .
.Правильность вычислений подтверждается проверкой
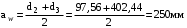 , что верно.
, что верно.Диаметры вершин зубьев
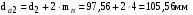 ,
,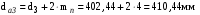 .
.Диаметры впадин зубьев
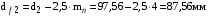 ,
,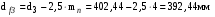 .
.Ширина колеса
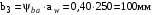 .
.Ширина шестерни
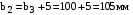 .
.Коэффициент ширины шестерни по диаметру
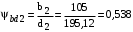 .
.3.3 Проверочный расчёт прочности зубьев
3.3.1 Расчётное контактное напряжение для косозубых цилиндрических передач /2, с.31/
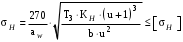 , (3.11)
, (3.11)где
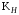
– коэффициент нагрузки; b – ширина колеса расчётная (наименьшая).
Остальные символы в формуле расшифрованы ранее.
Окружная скорость колёс
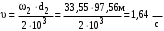 .
.При такой скорости
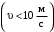 назначаем восьмую степень точности /2, с.32/.
назначаем восьмую степень точности /2, с.32/.Коэффициент нагрузки /2, с.32/ при проверочном расчёте на контактную прочность
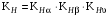 , (3.12)
, (3.12)где
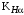 – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями;
– коэффициент, учитывающий неравномерность распределения нагрузки между зубьями; 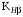 – коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба (по ширине венца);
– коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба (по ширине венца);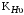 – коэффициент, учитывающий дополнительные динамические нагрузки (динамический коэффициент).
– коэффициент, учитывающий дополнительные динамические нагрузки (динамический коэффициент).По рекомендациям /2, с.39, 40/ назначаем следующие значения перечисленных коэффициентов:
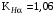 при окружной скорости
при окружной скорости 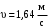 и восьмой степени точности;
и восьмой степени точности; 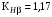 при значении коэффициента
при значении коэффициента 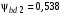 , твёрдости зубьев менее НВ 350 и несимметричном расположении колёс относительно опор;
, твёрдости зубьев менее НВ 350 и несимметричном расположении колёс относительно опор; 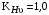 при окружной скорости
при окружной скорости 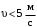 , восьмой степени точности и твёрдости менее НВ 350.
, восьмой степени точности и твёрдости менее НВ 350.Расчёт по формуле (3.1) даёт
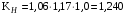 .
.Ширину колеса берём в расчёт минимальную b = 100 мм. Момент на колесе Т3 = 739,85 Н·м.
Расчёт по формуле (3.11) даёт
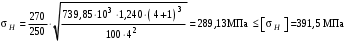 .
.Условие прочности выполняется. Недогрузка составляет
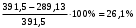 . Она объясняется увеличением первоначально вычисленного межосевого расстояния до стандартного
. Она объясняется увеличением первоначально вычисленного межосевого расстояния до стандартного  .
.3.3.2 Расчёт зубьев на контактную прочность по формуле (3.11) при кратковременных перегрузках моментом
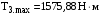 (см. раздел 2) даёт
(см. раздел 2) даёт