Файл: Введение 1 Изучение колебательных явлений в курсе физики средней школы как методическая проблема.docx

Введение

1 Изучение колебательных явлений в курсе физики средней школы как методическая проблема

1.1 Научно-методический анализ содержания раздела «Механические колебания»

1.1.1 Свободные колебания в системах без трения: математический и пружинный маятники

Изучение колебаний начинают с введения понятия о колебательном движении, которое является одним из основных в этой теме. Учащиеся уже знакомы с периодическими, т. е. повторяющимися через равные промежутки времени, движениями (например, с равномерным движением по окружности).

Разновидность периодического движения – колебательное, т. е. такое движение, при котором тело перемещается от своего положения равновесия то в одну сторону, то в другую. Приводят примеры колебательных движений и демонстрируют системы тел, в которых при определенных условиях могут существовать колебания (вертикальный и горизонтальный пружинные маятники, груз на нити, ножовочное полотно, зажатое в тисках, и др.).

На примере этих колебательных систем подчеркивают то общее, что характерно для любых из них: наличие устойчивого положения равновесия фактор инертности, обеспечивающий прохождение телом положения равновесия и, таким образом, установление колебательного движения вместо простого возвращения тела в положение равновесия, и, наконец, достаточно малое трение в системе.


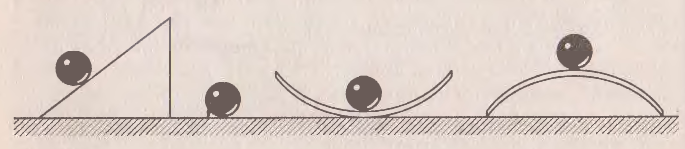
Рисунок 1 – Различные системы.

Учащиеся убеждаются в наличии этих признаков у каждой из демонстрируемых колебательных систем. После этого им можно предложить ответить па вопрос, могут ли возникнуть колебания в системах, представленных на рисунке 1, и проверить свой ответ экспериментально.

Вводят понятие о свободных колебаниях. Колебания, возникающие в системе, выведенной из положения равновесия и представленной самой себе, называют свободными. Если в системе отсутствует трение, то свободные колебания называют собственными, они происходят с собственной частотой, которая определяется только параметрами системы. Колебательная система, лишенная трения, ­ идеализация, но при малом коэффициенте затухания различие между свободными и собственными колебаниями слишком незначительно, чтобы его учитывать (при добротности системы в несколько единиц оно не превышает нескольких процентов). Поэтому в школьном преподавании физики понятия свободных и собственных колебаний не разграничивают и учащиеся знакомятся только с понятием свободных колебаний.

Одно из важнейших понятий теории колебаний – гармоническое колебание. Это понятие широко используют по двум причинам: любое периодическое негармоническое движение может быть представлено в виде суммы ряда гармонических колебаний кратных частот, причем эти последние можно выделить и наблюдать. Кроме того, существует много таких колебательных систем, колебания которых с большой точностью можно считать гармоническими.

Программа общеобразовательной средней школы обычно предполагала впервые ознакомить школьников с понятием гармонического колебания в последнем классе средней школы при изучении электромагнитных колебаний. Но существует реальная возможность сделать это уже при изучении механических колебаний.

При этом возможен следующий подход: используя связь равномерного движения по окружности и колебательного движения, получают закон изменения координаты гармонически колеблющегося тела со временем 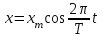.Для этого вначале на опыте показывают, что тень от шарика, равномерно движущегося по окружности, совершает колебательное движение (рисунок 2).


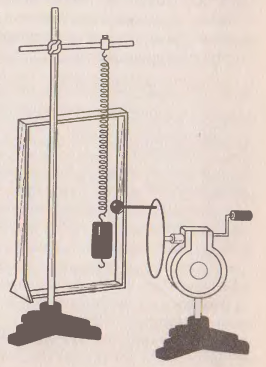
Рисунок 2 ­ Установка для эксперимента с пружинным маятником и шариком.

На установке возбуждают колебания пружинного маятника. Убеждаются в том, что маятник совершает такие же колебания, что и тень на экране от шарика, при этом частоту вращения шарика подбирают таким образом, чтобы колебания были синхронными.

Затем учащиеся самостоятельно выполняют задание: найти выражение для координаты проекции на ось X материальной точки А. движущейся равномерно со скоростью 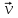по окружности (рис. 3).


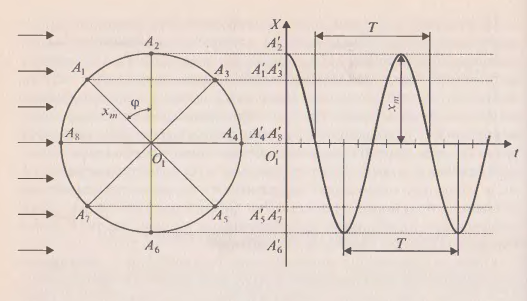
Рисунок 3 ­ Равномерное движение материальной точки A со скоростью 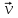по окружности

Получают выражение 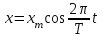. Сообщают, что движение, в котором координата тела меняется по такому закону, называют гармоническим колебанием. Так как маятник и тень шарика на экране совершают одинаковое движение (колеблются синхронно), делаем вывод: колебания маятника могут быть описаны тем же уравнением, т.е. при определенных условиях они тоже являются гармоническими. В завершающем обучение классе при изучении электромагнитных колебаний это определение можно расширить, показав, что любая величина, изменяющаяся по такому закону, совершает гармоническое колебание (например, заряд конденсатора в контуре, сила тока и напряжение в контуре и др.).

Возможен и другой подход к введению понятия о гармоническом колебании: рассматривают динамику свободных колебаний пружинного (рис. 4, а) и математического (рис. 4, б) маятников под действием соответственно силы упругости и силы тяжести в отсутствие силы трения. Для каждого из этих случаев на чертеже изображают силы, действующие на маятник, и записывают уравнение движения в проекциях на ось OX маятника, выведенного из положения равновесия и предоставленного самому себе, из которого получают 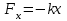(для пружинного маятника) и 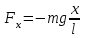(для математического).


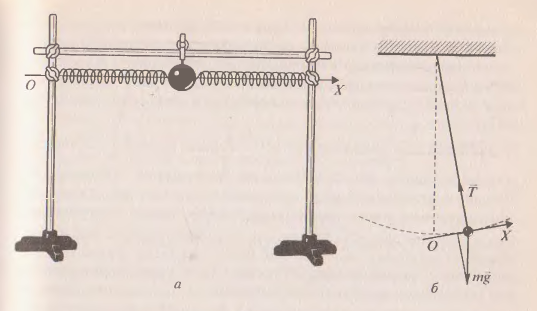
Рисунок 4 ­ Маятники: а) пружинный; б) математический.

Вводят определение: механические колебания, которые совершаются под действием силы, пропорциональной смещению и направленной к положению равновесия, называют гармоническими.

Если из динамических уравнений выразить ускорение (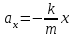 и 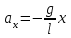), то может быть дано и такое определение: движение, при котором ускорение прямо пропорционально отклонению материальной точки от положения равновесия и всегда направлено в сторону равновесия, называют гармоническим колебанием.

Под руководством учителя анализируют динамическое уравнение колебания маятников. Обращают внимание на общие черты этих уравнений, их внешнее сходство – уравнения 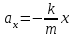и 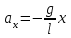линейны, коэффициенты при координате х постоянны и не зависят ни от самой координаты, ни от ускорения.

Следует обратить внимание школьников на то, что гармонические колебания ­ качественно новый вид движения, в котором ускорение непрерывно изменяется по модулю и направлению. Полезно провести анализ зависимости ускорения маятников от смещения и сравнить гармоническое колебание с уже известными учащимся видами движения – прямолинейным (равномерным и равноускоренным) и равномерным движением по окружности.

При анализе уравнения 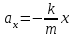(или 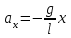) обращают внимание на то, что при большой деформации пружины (или большом отклонении нити маятника от положения равновесия) нарушается прямая пропорциональность между ускорением и смещением. Постоянный коэффициент 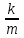(или 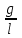) становится зависимым от деформации пружины (или угла отклонения нити), уравнение перестает быть линейным – движение будет периодическим, но не гармоническим. Таким образом, приходим к выводу: при отсутствии рассеяния энергии и достаточно малых амплитудах свободные колебания маятников являются гармоническими.

Введение основных характеристик колебательного движения – амплитуды, частоты и периода – может последовать сразу после того, как рассмотрены свободные колебания маятников и введено понятие гармонического колебания. Строго говоря, понятие частоты применимо только для гармонических колебаний, т.е. для бесконечных во времени процессов. В случае периодических процессов негармонического характера (а именно с ними чаще всего приходится встречаться) мы имеем дело не с частотой, а с целым набором (полосой) частот.

Вводят понятие амплитуды, частоты и периода колебаний, причем подчеркивают, что именно эти величины, а не смещение, скорость и ускорение колеблющейся точки в данный момент времени характеризуют колебательный процесс в целом. Для усвоения понятий амплитуды, периода и частоты колебаний необходимо предложить учащимся ряд упражнений различного характера – качественных, количественных, связанных с проведением экспериментов.

Формулы для периода колебаний математического и пружинного маятников не могут быть строго выведены из-за отсутствия необходимой математической подготовки учащихся. Поэтому они могут быть даны в готовом виде (с последующей экспериментальной проверкой) или выведены косвенным путем.

Например, формулу периода колебаний математического маятника можно получить, используя экспериментальный фат, установленный еще X. Гюйгенсом: конический маятник длиной l совершает полный оборот за тот же промежуток времени, в течение которого математический маятник той же длины совершает полное колебание, т.е. за период. Перед учащимися можно поставить задачу: воспользовавшись этим опытным фактом, найти формулу периода колебания математического маятника.

Для лучшего усвоения формулы периода колебаний маятников (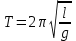 и 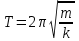) ее следует проверить на опыте, показав, что от коэффициента упругости и массы груза, так же как и от ускорения свободного падения и длины нити для математического маятника, зависит собственная частота колебаний системы.

1.1.2 Колебания в системах при наличии трения

Наличие сил трения приводит к уменьшению энергии колебательной системы и убыванию амплитуды колебаний. Замедляя движение, силы трения увеличивают период, т.е. уменьшает частоту колебаний. Такие колебания не будут гармоническими, механическая энергия постепенно расходуется на совершение работы по преодолению силы сопротивления воздуха и превращается во внутреннюю энергию. Чем больше сила сопротивлению движению, тем быстрее прекращаются свободные колебания. В более вязких средах, например, в воде колебания затухают быстрее, чем в воздухе. Такие колебания называются затухающими.

Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс в природе невозможен. Свободные колебания любого маятника рано или поздно затухают и прекращаются. Поэтому в практической деятельности обычно встречаются именно с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний x_m является убывающей функцией. В реальных колебательных системах помимо возвращающей силы действуют силы сопротивления среды.

Поскольку скорость движения при колебаниях небольшая, будем считать, что сила сопротивления пропорциональна скорости движения F_с υ:

---

F_c = – r ×υ = – r × ,

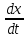где r- коэффициент сопротивления среды;

На основании II закона Ньютона, учитывая действие сил сопротивления и сил упругости, получим:

m×a = – r × x – r × υ

,

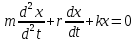Если разделить правую и левую часть на m и ввести обозначения 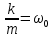, а 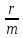= 2β, то получим, что решением такого уравнения будет функция:

x = x_m×e^-βt×Cos(ωt+φ₀).

Эта зависимость является уравнением свободных затухающих колебаний, в котором амплитуда убывает по экспоненциальному закону.

Период таких затухающих колебаний равен:

T = .

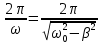Степень убывания амплитуды определяется коэффициентом затухания колебаний β

β =

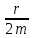
За время t = 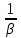амплитуда уменьшается в e ≈ 2,72 раз.

1.1.3 Вынужденные колебания. Резонанс

Изучение вынужденных колебаний можно начать с примеров тел (систем тел), в которых колебания происходят под действием периодической внешней силы: колебания иглы швейной машины, колебания поршня в двигателе внутреннего сгорания, различные вибрационные машины (для погружения свай в грунт, для сортировки и транспортировки, для уплотнения материала, например бетона и т.д.) Сообщают, что такие колебания называют вынужденными. Наибольший интерес представляют случаи, когда периодическая внешняя сила действует на систему, в которой могут происходить свободные колебания. Демонстрируют опыт, в котором вынужденные колебания совершаются пружинным маятником. С помощью установки с горизонтальным маятником (рис. 7) показывают существование собственных колебаний в системе и предлагают учащимся оценить собственную частоту колебаний ω₀.


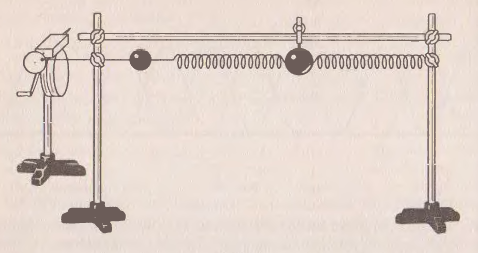
Рисунок 5 ­ Горизонтальный маятник.
Далее демонстрируют вынужденные колебания под действием периодической внешней силы с частотой ω, и школьники наблюдают вначале сложное движение маятника, в котором собственные колебания со временем затухают, а затем в установившемся движении маятник совершает уже только вынужденные колебания с частотой ω. Показывают, что при частоте внешней силы, превышающей собственную частоту ω

---

₀ системы, установившиеся колебания маятника также происходят с частотой ω. Таким образом, вынужденные колебания под действием периодической внешней силы совершаются с частотой этой силы. Можно предложить школьникам провести сравнение свободных и вынужденных колебаний в одной и той же системе, объяснить, почему вынужденные колебания не затухают.

Наибольший интерес при изучении вынужденных колебаний представляет явление резонанса. На той же установке (см. рис. 5) наблюдают резкое возрастание амплитуды вынужденных колебаний в случае, когда частота вынуждающей силы приближается к собственной частоте колебаний ω₀ системы. Такое возрастание амплитуды при совпадении собственной частоты колебаний и частоты вынуждающей силы называют резонансом.

Если на той же установке продолжать и дальше увеличивать частоту вынуждающей силы, то можно показать, что амплитуда вынужденных колебаний начинает уменьшаться – при очень высоких частотах из-за инертности системы она может стать очень малой.

Необходимо остановиться на причинах резкого возрастания амплитуды при резонансе. На той же установке можно показать, что при резонансе сила и смещение в любой момент времени совпадают по направлению. Это означает, что вынуждающая сила в течение периода совершает максимальную положительную работу, так как, совпадая по направлению со смещением тела, она все время «подталкивает» его, наиболее сильно раскачивая систему. Энергия источника расходуется на преодоление сопротивления и увеличение амплитуды. Но с ростом амплитуды колебаний возрастает сила сопротивления, поэтому всё большая часть энергии расходуется на ее преодоление [9]. При резонансе амплитуда достигает такого значения, что энергия, которая продолжает поступать от источника в систему, целиком расходуется на преодоление сопротивления. Таким образом, амплитуда при резонансе зависит от значения сопротивления в системе [6].

Резонанс можно демонстрировать с помощью метронома и нитяного маятника (рис. 6). Нитяной маятник нитью соединяют с маятником метронома. Па опыте наблюдают, что при совпадении собственной частоты колебаний нитяного маятника и маятника метронома амплитуда колебаний нитяного маятника максимальна.


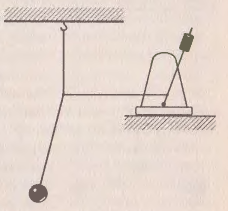
Рисунок 6 ­ Метроном и нитяной маятник

Особое внимание следует уделить учету и использованию резонансных явлений в жизни. Приводят примеры вредного влияния резонанса (разрушение опор под неуравновешенными конструкциями, например, под плохо центрированным двигателем, при работе которого в опорах возбуждаются вынужденные колебания, и др.), указывают основные пути предотвращения резонанса – изменение собственной частоты колебаний системы и использование демпферов – гасителей колебаний.

---

1.1.4 Автоколебания

Автоколебания ­ незатухающие колебания в диссипативной динамической системе с нелинейной обратной связью, поддерживающиеся за счёт энергии постоянного, то есть непериодического внешнего воздействия. Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.

В автоколебательной системе можно выделить три характерных элемента – колебательная система, источник энергии и устройство обратной связи между колебательной системой и источником. В качестве колебательной системы может быть использована любая механическая система, способная совершать собственные затухающие колебания (например, маятник настенных часов). Источником энергии может служить энергия деформация пружины или потенциальная энергия груза в поле тяжести. Устройство обратной связи представляет собой некоторый механизм, с помощью которого автоколебательная система регулирует поступление энергии от источника. На рисунке 7 изображена схема взаимодействия различных элементов автоколебательной системы.

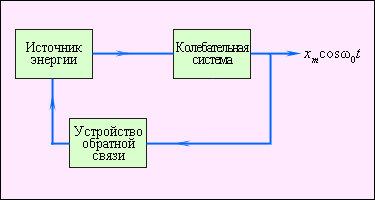Рисунок 7­ Функциональная схема автоколебательной системы

Примером механической автоколебательной системы может служить часовой механизм с анкерным ходом (рис. 8). Ходовое колесо с косыми зубьями жестко скреплено с зубчатым барабаном, через который перекинута цепочка с гирей. На верхнем конце маятника закреплен анкер (якорек) с двумя пластинками из твердого материала, изогнутыми по дуге окружности с центром на оси маятника. В ручных часах гиря заменяется пружиной, а маятник – балансиром – маховиком, скрепленным со спиральной пружиной.

Балансир совершает крутильные колебания вокруг своей оси. Колебательной системой в часах является маятник или балансир. Источником энергии – поднятая вверх гиря или заведенная пружина. Устройством, с помощью которого осуществляется обратная связь, является анкер, позволяющий ходовому колесу повернуться на один зубец за один полупериод.

---

Обратная связь осуществляется взаимодействием анкера с ходовым колесом. При каждом колебании маятника зубец ходового колеса толкает анкерную вилку в направлении движения маятника, передавая ему некоторую порцию энергии, которая компенсирует потери энергии на трение. Таким образом, потенциальная энергия гири (или закрученной пружины) постепенно, отдельными порциями передается маятнику.

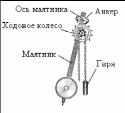Рисунок 8 ­ Часовой механизм с маятником

Автоколебания лежат в основе многих явлений природы:

­ колебания листьев растений под действием равномерного потока воздуха;

­ образование турбулентных потоков на перекатах и порогах рек;

_­ голоса людей, животных и птиц образуются благодаря автоколебаниям, возникающим при прохождении воздуха через голосовые связки;

­ действие регулярных гейзеров и пр.

1.1.5 Параметрические колебания

Параметрические колебания отличаются от вынужденных характером внешнего воздействия. Они вызываются периодическим изменением извне какого-либо физического параметра системы (например, массы), однако при вынужденных колебаниях задана сила или какая-либо другая величина, совершающая колебания, а параметры системы остаются постоянными.

Параметрические колебания определяются изменением во времени параметров системы; пример - колебание груза, закрепленного на горизонтальной консольной балке при периодическом изменении длины консоли.

Параметрические колебания не затухают при наличии сил сопротивления. Поддержание параметрических колебаний происходит за счет подвода энергии внешними силовыми воздействиями, изменяющими физические параметры системы.

Однако существуют силы более сложной природы, в частности нестационарные позиционные силы, которые зависят от координат q₁, а также от времени t (в явном виде):
Q₁ = Q₁(q₁, q₂, ..., q_s, t) (j = 1, 2, …, s),
и притом так, что их невозможно представить в виде суммы двух слагаемых, одно из которых зависит только от координат, а другое — только от времени.

Ограничимся рассмотрением линейных систем с одной степенью свободы, когда при малых отклонениях от положения равновесия обобщенная сила определяется выражением
Q = -cq,
причем, в отличие от случаев действия стационарных восстанавливающих сил, параметр c = c(t) является функцией времени.

---