Файл: Введение 1 Изучение колебательных явлений в курсе физики средней школы как методическая проблема.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 11.01.2024

Просмотров: 87

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Введение 1 Изучение колебательных явлений в курсе физики средней школы как методическая проблема 1.1 Научно-методический анализ содержания раздела «Механические колебания» 1.1.1 Свободные колебания в системах без трения: математический и пружинный маятники Изучение колебаний начинают с введения понятия о колебательном движении, которое является одним из основных в этой теме. Учащиеся уже знакомы с периодическими, т. е. повторяющимися через равные промежутки времени, движениями (например, с равномерным движением по окружности). Разновидность периодического движения – колебательное, т. е. такое движение, при котором тело перемещается от своего положения равновесия то в одну сторону, то в другую. Приводят примеры колебательных движений и демонстрируют системы тел, в которых при определенных условиях могут существовать колебания (вертикальный и горизонтальный пружинные маятники, груз на нити, ножовочное полотно, зажатое в тисках, и др.).На примере этих колебательных систем подчеркивают то общее, что характерно для любых из них: наличие устойчивого положения равновесия фактор инертности, обеспечивающий прохождение телом положения равновесия и, таким образом, установление колебательного движения вместо простого возвращения тела в положение равновесия, и, наконец, достаточно малое трение в системе. Рисунок 1 – Различные системы.Учащиеся убеждаются в наличии этих признаков у каждой из демонстрируемых колебательных систем. После этого им можно предложить ответить па вопрос, могут ли возникнуть колебания в системах, представленных на рисунке 1, и проверить свой ответ экспериментально.Вводят понятие о свободных колебаниях. Колебания, возникающие в системе, выведенной из положения равновесия и представленной самой себе, называют свободными. Если в системе отсутствует трение, то свободные колебания называют собственными, они происходят с собственной частотой, которая определяется только параметрами системы. Колебательная система, лишенная трения, ­ идеализация, но при малом коэффициенте затухания различие между свободными и собственными колебаниями слишком незначительно, чтобы его учитывать (при добротности системы в несколько единиц оно не превышает нескольких процентов). Поэтому в школьном преподавании физики понятия свободных и собственных колебаний не разграничивают и учащиеся знакомятся только с понятием свободных колебаний.Одно из важнейших понятий теории колебаний – гармоническое колебание. Это понятие широко используют по двум причинам: любое периодическое негармоническое движение может быть представлено в виде суммы ряда гармонических колебаний кратных частот, причем эти последние можно выделить и наблюдать. Кроме того, существует много таких колебательных систем, колебания которых с большой точностью можно считать гармоническими.Программа общеобразовательной средней школы обычно предполагала впервые ознакомить школьников с понятием гармонического колебания в последнем классе средней школы при изучении электромагнитных колебаний. Но существует реальная возможность сделать это уже при изучении механических колебаний.При этом возможен следующий подход: используя связь равномерного движения по окружности и колебательного движения, получают закон изменения координаты гармонически колеблющегося тела со временем .Для этого вначале на опыте показывают, что тень от шарика, равномерно движущегося по окружности, совершает колебательное движение (рисунок 2). Рисунок 2 ­ Установка для эксперимента с пружинным маятником и шариком.На установке возбуждают колебания пружинного маятника. Убеждаются в том, что маятник совершает такие же колебания, что и тень на экране от шарика, при этом частоту вращения шарика подбирают таким образом, чтобы колебания были синхронными.Затем учащиеся самостоятельно выполняют задание: найти выражение для координаты проекции на ось X материальной точки А. движущейся равномерно со скоростью по окружности (рис. 3). Рисунок 3 ­ Равномерное движение материальной точки A со скоростью по окружностиПолучают выражение . Сообщают, что движение, в котором координата тела меняется по такому закону, называют гармоническим колебанием. Так как маятник и тень шарика на экране совершают одинаковое движение (колеблются синхронно), делаем вывод: колебания маятника могут быть описаны тем же уравнением, т.е. при определенных условиях они тоже являются гармоническими. В завершающем обучение классе при изучении электромагнитных колебаний это определение можно расширить, показав, что любая величина, изменяющаяся по такому закону, совершает гармоническое колебание (например, заряд конденсатора в контуре, сила тока и напряжение в контуре и др.).Возможен и другой подход к введению понятия о гармоническом колебании: рассматривают динамику свободных колебаний пружинного (рис. 4, а) и математического (рис. 4, б) маятников под действием соответственно силы упругости и силы тяжести в отсутствие силы трения. Для каждого из этих случаев на чертеже изображают силы, действующие на маятник, и записывают уравнение движения в проекциях на ось OX маятника, выведенного из положения равновесия и предоставленного самому себе, из которого получают (для пружинного маятника) и (для математического). Рисунок 4 ­ Маятники: а) пружинный; б) математический.Вводят определение: механические колебания, которые совершаются под действием силы, пропорциональной смещению и направленной к положению равновесия, называют гармоническими.Если из динамических уравнений выразить ускорение ( и ), то может быть дано и такое определение: движение, при котором ускорение прямо пропорционально отклонению материальной точки от положения равновесия и всегда направлено в сторону равновесия, называют гармоническим колебанием.Под руководством учителя анализируют динамическое уравнение колебания маятников. Обращают внимание на общие черты этих уравнений, их внешнее сходство – уравнения и линейны, коэффициенты при координате х постоянны и не зависят ни от самой координаты, ни от ускорения.Следует обратить внимание школьников на то, что гармонические колебания ­ качественно новый вид движения, в котором ускорение непрерывно изменяется по модулю и направлению. Полезно провести анализ зависимости ускорения маятников от смещения и сравнить гармоническое колебание с уже известными учащимся видами движения – прямолинейным (равномерным и равноускоренным) и равномерным движением по окружности.При анализе уравнения (или ) обращают внимание на то, что при большой деформации пружины (или большом отклонении нити маятника от положения равновесия) нарушается прямая пропорциональность между ускорением и смещением. Постоянный коэффициент (или ) становится зависимым от деформации пружины (или угла отклонения нити), уравнение перестает быть линейным – движение будет периодическим, но не гармоническим. Таким образом, приходим к выводу: при отсутствии рассеяния энергии и достаточно малых амплитудах свободные колебания маятников являются гармоническими.Введение основных характеристик колебательного движения – амплитуды, частоты и периода – может последовать сразу после того, как рассмотрены свободные колебания маятников и введено понятие гармонического колебания. Строго говоря, понятие частоты применимо только для гармонических колебаний, т.е. для бесконечных во времени процессов. В случае периодических процессов негармонического характера (а именно с ними чаще всего приходится встречаться) мы имеем дело не с частотой, а с целым набором (полосой) частот.Вводят понятие амплитуды, частоты и периода колебаний, причем подчеркивают, что именно эти величины, а не смещение, скорость и ускорение колеблющейся точки в данный момент времени характеризуют колебательный процесс в целом. Для усвоения понятий амплитуды, периода и частоты колебаний необходимо предложить учащимся ряд упражнений различного характера – качественных, количественных, связанных с проведением экспериментов.Формулы для периода колебаний математического и пружинного маятников не могут быть строго выведены из-за отсутствия необходимой математической подготовки учащихся. Поэтому они могут быть даны в готовом виде (с последующей экспериментальной проверкой) или выведены косвенным путем.Например, формулу периода колебаний математического маятника можно получить, используя экспериментальный фат, установленный еще X. Гюйгенсом: конический маятник длиной l совершает полный оборот за тот же промежуток времени, в течение которого математический маятник той же длины совершает полное колебание, т.е. за период. Перед учащимися можно поставить задачу: воспользовавшись этим опытным фактом, найти формулу периода колебания математического маятника.Для лучшего усвоения формулы периода колебаний маятников ( и ) ее следует проверить на опыте, показав, что от коэффициента упругости и массы груза, так же как и от ускорения свободного падения и длины нити для математического маятника, зависит собственная частота колебаний системы. 1.1.2 Колебания в системах при наличии трения Наличие сил трения приводит к уменьшению энергии колебательной системы и убыванию амплитуды колебаний. Замедляя движение, силы трения увеличивают период, т.е. уменьшает частоту колебаний. Такие колебания не будут гармоническими, механическая энергия постепенно расходуется на совершение работы по преодолению силы сопротивления воздуха и превращается во внутреннюю энергию. Чем больше сила сопротивлению движению, тем быстрее прекращаются свободные колебания. В более вязких средах, например, в воде колебания затухают быстрее, чем в воздухе. Такие колебания называются затухающими.Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс в природе невозможен. Свободные колебания любого маятника рано или поздно затухают и прекращаются. Поэтому в практической деятельности обычно встречаются именно с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний xm является убывающей функцией. В реальных колебательных системах помимо возвращающей силы действуют силы сопротивления среды. Поскольку скорость движения при колебаниях небольшая, будем считать, что сила сопротивления пропорциональна скорости движения Fс

1.2 Научно-методический анализ содержания раздела «Электромагнитные колебания»

Содержание



Если к выводам электрической цепи из последовательно соединенных активного сопротивления, конденсатора и катушки (рис.12) подвести переменное напряжение, то в цепи возникают вынужденные электрические колебания силы тока и напряжения.

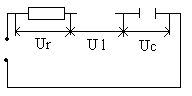
Рисунок 12 ­ Последовательное соединение активного сопротивления, конденсатора и катушки
Емкостное сопротивление ХС конденсатора и индуктивное сопротивление ХL катушки зависят от частоты ω приложенного напряжения. Поэтому при постоянной амплитуде Um колебаний напряжения амплитуда Im колебаний силы тока в цепи зависит от частоты ω переменного напряжения.

При постепенном увеличении частоты приложенного напряжения емкостное сопротивление ХС конденсатора уменьшается. Это приводит к возрастанию амплитуды колебаний силы тока.

Увеличение амплитуды колебаний силы тока в цепи при увеличении частоты приложенного напряжения продолжается до тех пор, пока индуктивное сопротивление катушки не станет равным емкостному сопротивлению конденсатора:


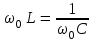
При выполнении условия данной формулы при равенстве индуктивного сопротивления катушки емкостному сопротивлению конденсатора, и одинаковой силе тока одинаковыми оказываются и амплитуды колебаний напряжения на конденсаторе и катушке. Колебания напряжения на катушке и конденсаторе противоположны по фазе, поэтому сумма напряжений на них при выполнении условия данной формулы в любой момент времени равна нулю. В результате напряжение на активном сопротивлении при резонансе оказывается равным полному напряжению:

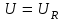
А сила тока в цепи достигает максимального значения, то есть наступает резонанс.

То есть при дальнейшем увеличении частоты индуктивное сопротивление катушки начинает превышать емкостное сопротивление конденсатора. Увеличение индуктивного сопротивления приводит к уменьшению амплитуды колебаний силы тока (рис.13).


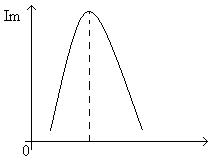
Рисунок 13 ­ Амплитуда силы тока при резонансе
Из уравнения (1) следует, что электрический резонанс в последовательной цепи, содержащей конденсатор и катушку, наступает при частоте ω0, равной:



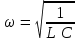
Видно из выражения, что резонансная частота ω0 электрической цепи совпадает с собственной частотой свободных электрических колебаний в этой цепи.

Резонансом в электрическом колебательном контуре называется явление резкого возрастания, амплитуды вынужденных колебаний силы тока при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура.

Явление электрического резонанса используется при осуществлении радиосвязи. Радиоволны от различных передающих станций возбуждают в антенне радиоприемника переменные токи различных частот, так как каждая передающая радиостанция работает на своей частоте. С антенной индуктивно связан колебательный контур. Вследствие электромагнитной индукции в контурной катушке возникают переменные ЭДС соответствующих частот и вынужденные колебания силы тока этих же частот. Но только при резонансе колебания силы тока в контуре и напряжения на контуре будут значительными. Имея это в виду, говорят, что из колебаний всех частот, возбужденных в антенне, контур выделяет только колебания, частота которых равна собственной частоте контура. Настройка контура на нужную частоту ω0 обычно осуществляется путем изменения емкости конденсатора. В этом и состоит настройка радиоприемника на определенную радиостанцию.


2. Использование идей единого подхода к изучению колебаний разной физической природы в средней школе

2.1 Единый подход к изучению физических явлений разной природы

2.2 Единый подход к изучению свободных механических и электромагнитных колебаний

2.3 Единый подход к изучению вынужденных механических и электромагнитных колебаний. Резонанс.

2.4 Проверка эффективности разработанной методики

Заключение

Список использованной литературы
Литература

1. Мякишев Физика 10-11

2. Касьянов Физика 10-11

3. Пинский Физика для физико-математическихпрофилей

4. Яворский и Пинский Основы физики
Абушкин Общая и экспериментальная физика. Механика
Другие вузовский учебники физики (Савельев, Сивухин , Стрелков)
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ

ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ ИМЕНИ М.Е. ЕВСЕВЬЕВА»

Физико-математический факультет
Кафедра физики и методики обучения физике
УТВЕРЖДАЮ

Зав. кафедрой

канд. пед. наук, доцент

А. А. Харитонова

«___» ___________2020 г.

ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА

(БАКАЛАВРСКАЯ РАБОТА)
ИЗУЧЕНИЕ ЗАКОНОВ ВОЛНОВОЙ ОПТИКИ С ИСПОЛЬЗОВАНИЕМ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ В СРЕДНЕЙ ШКОЛЕ
Автор работы __________________________________________ Н. Н. Петров
Направление подготовки 44.03.05 Педагогическое образование (с двумя профилями подготовки)

Профиль Физика. Информатика
Руководитель работы

канд. пед. наук, профессор _______________________________ Х. Х. Абушкин
Нормоконтролер

канд. филол. наук, доцент _______________________________ А. И. Новикова
Рецензент

канд. филол. наук, доцент _______________________________ И. И. Михайлов
Саранск 2021

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ

ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ ИМЕНИ М.Е. ЕВСЕВЬЕВА»
Физико-математический факультет

Кафедра физики и методики обучения физике
УТВЕРЖДАЮ

Зав. кафедрой

канд. пед. наук, доцент

А. А. Харитонова

«___» ___________2020 г.

ЗАДАНИЕ НА ВЫПУСКНУЮ КВАЛИФИКАЦИОННУЮ РАБОТУ

на степень БАКАЛАВРА
Студент Петров Никита Николаевич группа МДФ-116
1. Тема: «Изучение законов волновой оптики с использованием компьютерного моделирования в средней школе»

Утверждена приказом по МордГПИ № 3350 от 09.12.2015 г.

2. Срок представления к защите: 28.04.2021

3. Исходные данные для выпускной квалификационной работы: издательские системы, периодические публикации, электронные источники.

4. Содержание выпускной квалификационной работы:

4.1 Введение

4.2 Использование компьютерного моделирования при изучении раздела «Волновая оптика» как методическая проблема

4.2.1 Нaучнo-мeтoдичeский анализ содержания раздела «Волновая оптика

4.2.1.1 Свет как электромагнитная волна.

4.2.1.2 Дисперсия световых волн

4.2.1.3 Интерференция света

4.2.1.4 Дифракция света

4.2.1.5 Поляризация

4.2.2 Компьютерное моделирование в образовании

4.3 Методика изучения волновых явлений на основе педагогических программных средств

4.3.1 Применение информационных и компьютерных технологий в обучении физике

4.3.2 Разработка педагогических программных средств по изучению основных волновых явлений в средней школе с использованием MATCAD


4.3.3 Проверка эффективности разработанной методики

4.3.4 Апробация методики изучения радела «Взаимодействие тел»

4.4 Заключение

4.5 Список использованных источников
Руководитель работы

канд. пед. наук, профессор________________________Х. Х. Абушкин
Задание принял к исполнению _____________________Н. Н. Петров
Аннотация

Выпускная квалификационная работа на степень бакалавра содержит 62 страницы, 44 использованных источника.

Данная бакалаврская работа посвящена изучению законов волновой оптики с использованием компьютерного моделирования в средней школе.

Бакалаврская работа включает нaучнo-мeтoдичeский анализ содержания раздела «Волновая оптика» и роль компьютерного моделирования в образовании; применение информационных и компьютерных технологий в обучении физике. Представлена методическая разработка конспекта урока с применением педагогических программных средств, компьютерные модели «Кольца Ньютона» и «Дифракция на щели», разработанные в системе MATCAD.

Объект исследования: процесс обучения физике в средней школе.

Предмет исследования: методика изучения законов волновой оптики в средней школе с использованием компьютерных моделей.

Целью исследования является разработка методики обучения законам волновой оптики в средней школе с использованием компьютерных моделей.

В процессе работы использовались методы: анализ учебной и научной литературы, источников интернет; метод проектов, методы математической статистики.

В результате исследования определены роль и место педагогических программных средств при изучении раздела «Волновая оптика».

Степень внедрения – частичная.

Область применения – использование в школьной практике при изучении раздела «Волновая оптика».

Эффективность – повышение качества знаний учащихся по разделу «Волновая оптика».

Содержание




Введение 1

1 Изучение колебательных явлений в курсе физики средней школы как методическая проблема 1

1.1 Научно-методический анализ содержания раздела «Механические колебания» 1

1.1.1 Свободные колебания в системах без трения: математический и пружинный маятники 1

1.1.2 Колебания в системах при наличии трения 7

1.1.3 Вынужденные колебания. Резонанс 9

1.1.4 Автоколебания 11

1.1.5 Параметрические колебания 13

1.2 Научно-методический анализ содержания раздела «Электромагнитные колебания» 15

1.2.1 Свободные электромагнитные колебания в идеализированных колебательных системах – колебательный контур 15

1.2.2 Электромагнитные колебания в реальном колебательном контуре 19

1.2.3 Вынужденные электромагнитные колебания в реальных системах. Электрический резонанс 21

Смотрите также файлы