Файл: Основные этапы в информационном развитии общества. Информационные революции.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 383
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Представление текстовых данных.
Представление звуковой информации.
Основные принципы формальной логики. Понятие законов логики
[править]Свойства логических операций
3. На что следует обратить особое внимание или вопросы безопасности
Графический интерфейс пользователя
Растровые графические редакторы
Цифровое оборудование для создания растровых графическихобъектов
Билет №15
операции алгебры логики
Логические операции
Простейшим и наиболее широко применяемым примером такой алгебраической системы является множество B, состоящее всего из двух элементов:
B = { Ложь, Истина }
Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций.
Опираясь на этот математический инструментарий, логика высказываний изучает высказывания и предикаты. Также вводятся дополнительные операции, такие как эквивалентность
Логика высказываний послужила основным математическим инструментом при создании компьютеров. Она легко преобразуется в битовую логику: истинность высказывания обозначается одним битом (0 — ЛОЖЬ, 1 — ИСТИНА); тогда операция
Впоследствии булева алгебра была обобщена от логики высказываний путём введения характерных для логики высказываний аксиом. Это позволило рассматривать, например, логику кубитов, тройственную логику (когда есть три варианта истинности высказывания: «истина», «ложь» и «не определено») и др.
[править]Свойства логических операций
-
Коммутативность: x y = y
y = y x,
x, 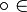 {&,
{&, 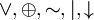 }.
}. -
Идемпотентность: x x = x,
x = x, 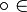 {&,
{&,  }.
}. -
Ассоциативность: (x y)
y) z = x
z = x (y
(y z),
z), 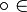 {&,
{&, 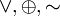 }.
}. -
Дистрибутивность конъюнкций и дизъюнкции относительно дизъюнкции, конъюнкции и суммы по модулю два соответственно:
-
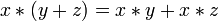 ,
, -
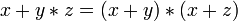 ,
, -
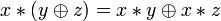 .
.
Законы де Мо́ргана:
-
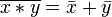 ,
, -
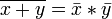 .
.
Законы поглощения:
-
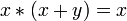 ,
, -
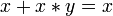 .
.
Другие (1):
-
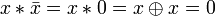 .
. -
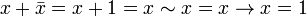 .
. -
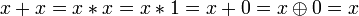 .
. -
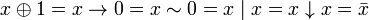 .
. -
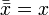 .
.
Другие (2):
-
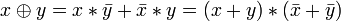 .
. -
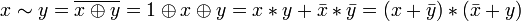 .
. -
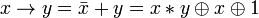 .
. -
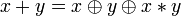
Другие (3) (Дополнение законов де Мо́ргана):
-
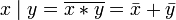 .
. -
 .
.
Существуют методы упрощения логической функции: например, Карта Карно, метод Куайна - Мак-Класки
Билет №16
основные законы преобразования алгебры логики
В алгебре логики имеются законы, которые записываются в виде соотношений. Логические законы позволяют производить равносильные (эквивалентные) преобразования логических выражений. Преобразования называются равносильными, если истинные значения исходной и полученной после преобразования логической функции совпадают при любых значениях входящих в них логических переменных.
Для простоты записи приведем основные законы алгебры логики для двух логических переменных А и В. Эти законы распространяются и на другие логические переменные.
1. Закон противоречия:
2. Закон исключенного третьего:
3. Закон двойного отрицания:
4. Законы де Моргана:
5. Законы повторения: A & A = A; A v A = A; В & В = В; В v В = В.
6. Законы поглощения: A ? (A & B) = A; A & (A ? B) = A.
7. Законы исключения констант: A ? 1 = 1; A ? 0 = A; A & 1 = A; A & 0 = 0; B ? 1 = 1; B ? 0 = B; B & 1 = B; B & 0 = 0.
8. Законы склеивания:
9. Закон контрапозиции: (A ? B) = (B ? A).
Для логических переменных справедливы и общематематические законы. Для простоты записи приведем общематематические законы для трех логических переменных A, В и С:
1. Коммутативный закон: A & B = B & A; A ? B = B ? A.
2. Ассоциативный закон: A & (B & C) = (A & B) & C; A ? (B ? C) = (A ? B) ? C.
3. Дистрибутивный закон: A & (B ? C) = (A & B) ? (A & C).
Как уже отмечалось, с помощью законов алгебры логики можно производить равносильные преобразования логических выражений с целью их упрощения. В алгебре логики на основе принятого соглашения установлены следующие правила (приоритеты) для выполнения логических операций: первыми выполняются операции в скобках, затем в следующем порядке: инверсия (отрицание), конъюнкция ( & ), дизъюнкция (v), импликация (?), эквиваленция (?)
Билет №17
построение таблиц истинности, логические законы
Порядок выполнения логических операций в сложном логическом выражении:
инверсия;
конъюнкция;
дизъюнкция;
импликация;
эквивалентность.
Для изменения указанного порядка выполнения операций используются скобки.
Алгоритм построения таблиц истинности для сложных выражений: