Файл: Методические рекомендации для обучающихся к выполнению практических работ по учебной дисциплине.docx
Добавлен: 12.01.2024
Просмотров: 192
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ТЕМА5.2. Многогранники.
Практическая работа № 23
Построение сечений многогранников.
Цель: закрепление знаний, отработка навыков построения сечений.
Пояснения к работе: При построении сечений следует руководствоваться следующими правилами: 1) 2 точки, лежащие в одной плоскости, можно соединять прямой линией; 2) Стороны сечения, лежащие в параллельных плоскостях – параллельны.
Задания к практической работе. (Постройте самостоятельно)
| Вариант 1 | Вариант 2 |
| 1. Высота прямой четырёхугольной пирамиды равна 4. Основание – прямоугольник со сторонами 2 и 8. Найти площади диагональных сечений. | 1. Высота правильной четырёхугольной пирамиды равна 4, диагональ 5 см. Найти площадь диагонального сечения. |
| 2. В правильной треугольной усеченной пирамиде стороны оснований равны 8 м и 5 м, а высота 3 м.  Провести сечение через сторону нижнего основания и противоположную ей вершину верхнего основания. Определить площадь сечения. Провести сечение через сторону нижнего основания и противоположную ей вершину верхнего основания. Определить площадь сечения. | 2. В правильной четырёхугольной усеченной пирамиде стороны оснований равны 6 см и 8 см, а боковое ребро 10 см. Провести сечение через конец диагонали меньшего основания перпендикулярно к этой диагонали и определить его площадь. |
| 3. В правильной четырёхугольной усеченной пирамиде площади оснований G и g, а боковое ребро образует с плоскостью нижнего основания угол в 45  Определить площадь диагонального сечения. Определить площадь диагонального сечения. | 3. В правильной треугольной усеченной пирамиде сторона большего основания a, сторона меньшего b. Боковое ребро образует с основанием угол в 45  Провести сечение через боковое ребро и ось и найти его площадь. Провести сечение через боковое ребро и ось и найти его площадь. |
| 4. Сторона основания правильной треугольной призмы равна 12 см, а высота призмы 6 см. Найдите площадь сечения этой призмы плоскостью, проходящей через сторону нижнего основания и противолежащую вершину верхнего основания призмы. | |
Критерии оценки:
«5» ставится за 4 верно решенных заданий;
«4» ставится за 3 верно решенных задания;
«3» ставится за 2 верно решенных задания;
«2» - если решено менее 2 заданий.
Литература.
Атанасян Л.С., Бутузов В.Ф. Геометрия, 10–11: учебник для общеобразовательных учреждений: базовый и профильный уровни. 21-е изд. М.: Просвещение, 2012. 255с.: ил.
ТЕМА 5.2. Многогранники.
Практическая работа № 24
Объем параллелепипеда. Объем призмы.
Цель: закрепление знаний, отработка навыков решения задач, используя свойства призмы и пирамиды.
Пояснения к работе.
1. Изучите п. 194, 195,196, 197, 199, 200 (с. 339 – 347 ). Геометрия 7-11 Погорелов
2. Ответьте на вопросы:
а) Сформулируйте свойства объемов многогранников.
б) Запишите в тетрадях формулы объемов прямой и наклонной призм.
3. Найдите объем и площадь полной поверхности куба, длина диагонали грани которого равна
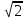 см.
см.4. Запишите формулу объема пирамиды.
5. Объем пирамиды ABC равен V. Найдите объем призмы, в основании которой лежит треугольник АВС, а высота равна высоте пирамиды.
6. Боковые ребра треугольной пирамиды попарно перпендикулярны, а длины их равны а, в, с. Найдите объем пирамиды.
7. Как изменится объем куба, если длину его ребра увеличить в два раза?
Задания к практической работе:
| 1. Каждое ребро прямого параллелепипеда имеет длину 5 см, один из углов основания 30  . Найдите объем и площадь полной поверхности параллелепипеда. . Найдите объем и площадь полной поверхности параллелепипеда.2. Стороны основания прямого параллелепипеда имеют длины 3 и 8 дм, а один из углов основания 120 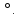 Найдите объем параллелепипеда и площади его диагональных сечений, если площадь его боковой поверхности равна 220 Найдите объем параллелепипеда и площади его диагональных сечений, если площадь его боковой поверхности равна 220 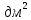 . .3. Дан прямой параллелепипед АВСД  , в котором В , в котором В 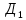 перпендикулярно перпендикулярно 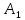 С. Найдите его объем, если В С. Найдите его объем, если В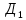 = 6 см, = 6 см, 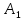 С = 8см АВ = 3 см С = 8см АВ = 3 см |
Критерии оценки:
«5» - ставится за три верно решенные задачи;
«4» - ставится за две верно решенные задачи;
«3» - ставится за одну верно решенную задачу;
«2» - менее одной задачи.
Литература.
Атанасян Л.С., Бутузов В.Ф. Геометрия, 10–11: учебник для общеобразовательных учреждений: базовый и профильный уровни. 21-е изд. М.: Просвещение, 2012. 255с.: ил.
Тема 5.3. Тела и поверхности вращения
Практическая работа № 25
Объемы и поверхности тел вращения.
Цель: контроль и закрепление знаний, умений, навыков студентов по теме объёмы и поверхности тел вращения.
Задания к практической работе.
| Вариант 1 | Вариант 2 |
| 1. Найдите полную и боковую поверхности цилиндра, длину диагонали осевого сечения, объем цилиндра, если радиус основания равны 4см, а высота равна 6см. | 1. Космический корабль имеет форму цилиндра высотой 7м и радиусом 3м, который с одной стороны завершен полусферой, а с другой – конусом высотой 4м. Найдите объем космического корабля. |
| 2. Высота и радиус конуса равны 5 см. Найдите длину образующей и боковую поверхность конуса. | 2. Угол между двумя образующими конуса – 60°, а угол между радиусами, проведёнными к основаниям образующих – 90°, радиус основания – 1см. Найдите объем конуса, полную поверхность конуса. |
| 3. Определите радиус шара, если его объем равен 4,4 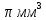 . . | 3. Найдите объем и полную поверхность шара , радиус которого 2 см. |
Критерии оценки: «5» ставится за 3 верно решенных задания;
«4» ставится за 2 верно решенных задания;
«3» ставится за 1 верно решенное задание;
«2» – если решено менее 1 задания.
Литература.
Атанасян Л.С., Бутузов В.Ф. Геометрия, 10–11: учебник для общеобразовательных учреждений: базовый и профильный уровни. 21-е изд. М.: Просвещение, 2012. 255с.: ил.
Раздел 6. Начала математического анализа.
Тема 6.1. Последовательности.
Практическая работа № 26
Предел функции.
Цель: способствовать закреплению навыков вычисления пределов.
Функцию y=f(x) называют непрерывной в точке x=a, если выполняется тождество:
Функцию y = f(x) называют непрерывной в точке x = a, если предел функции при x
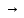 а равен значению функции в точке x = a.
а равен значению функции в точке x = a. Функция непрерывна на отрезке [a, b], если она непрерывна в каждой точке отрезка.
Пример 1. Вычислить:
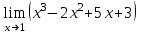 .
.Решение. Выражение х3 – 2х2 + 5х + 3 определено в любой точке х, в частности, в точке х = 1. Следовательно, функция у = х3 – 2х2 + 5х + 3 непрерывна в точке х = 1, а потому предел функции при стремлении х к 1 равен значению функции в точке х = 1.
Имеем:
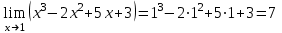 .
.Ответ: 7.
Для решения следующего примера нам потребуются правила вычисления предела функции в точке.
Правило 1.
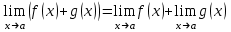 .
.Правило 2.
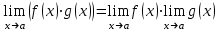 .
.Правило 3.
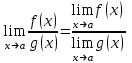 .
.Пример 2. Вычислить
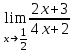 .
.Выражение
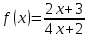 определено в любой точке х
определено в любой точке х 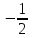 , в частности, в точке х =
, в частности, в точке х = 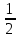 . Следовательно, функция у = f (x) непрерывна в точке х =
. Следовательно, функция у = f (x) непрерывна в точке х = 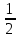 , значит предел функции при стремлении х к
, значит предел функции при стремлении х к 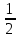 равен значению функции в точке х =
равен значению функции в точке х = 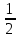 . Имеем:
. Имеем: