Файл: Методические рекомендации для обучающихся к выполнению практических работ по учебной дисциплине.docx
Добавлен: 12.01.2024
Просмотров: 188
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНО УЧРЕЖДЕНИЕ
«САХАЛИНСКОЙ ОБЛАСТИ ПОЛИТЕХНИЧЕСКИЙ ЦЕНТР № 2»
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
для обучающихся к выполнению практических работ
по учебной дисциплине:
Математика: алгебра и начала математического анализа; геометрия.
для специальности
35.02.06 «Технология производства и переработки сельскохозяйственной продукции»
Тымовское
2020
Практические работы по математике: алгебра и начала математического анализа; геометрия. Метод указ. / Сост. М.Г. Лашкевич / ГБОПУ СПЦ №2 Тымовское , 2018
Методические рекомендации по выполнению практических работ предназначены для организации работы на практических занятиях по учебной дисциплине:
Математика: алгебра и начала математического анализа; геометрия, которая является важной составной частью в системе подготовки квалифицированных рабочих, служащих среднего профессионального образования.
Методические рекомендации имеют практическую направленность и значимость.
Формируемые в процессе практических занятий умения могут быть использованы обучающимися в будущей профессиональной деятельности.
Методические рекомендации предназначены для обучающихся средних профессиональных учебных заведений, изучающих учебную дисциплину: «Математика: алгебра и начала математического анализа; геометрия» и могут использоваться на учебных занятиях.
Рекомендовано методической комиссией преподавателей ГБПОУ СПЦ №2
Председатель МК Г. В. Мартыновских
Содержание
1. Пояснительная записка…………………………………………………….. 3
2. Планирование практических работ……………………………………… 4
3. Методические рекомендации по выполнению практических работ….. 6
4. Литература……………………………………………………………….. 40
Пояснительная записка
Практические занятия служат связующим звеном между теорией и практикой, которые необходимы для закрепления теоретических знаний, полученных на уроках теоретического обучения, а так же для получения практических знаний.
Практические задания выполняются студентом или обучающимся самостоятельно, с применением знаний и умений, полученных на уроках, а так же с использованием необходимых пояснений, полученных от преподавателя при выполнении практического задания.
Практические задания разработаны в соответствии с учебной программой
Зачет по каждой практической работе получают после её выполнения, а также ответов на вопросы преподавателя, если таковые возникнут при проверке выполненного задания.
Компетенции
ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.
ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.
ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий.
ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.
Планирование практических работ
| № п/п | Разделы,темы, включая названия практических и лабораторных работ | ОК ПК |
| | Раздел 1 Алгебра | |
| | Тема 1.1. Развитие понятия о числе. | |
| 1 | П.З. № 1 Действия над натуральными, целыми, рациональными и действительными числами. | Ок 1-4 |
| 2 | П.З. № 2 Приближенные вычисления. Приближенное значение величины. Действия с приближенными числами. | Ок 1-4 |
| | Тема 1.2. Корни, степени и логарифмы. | |
| 3 | П.З. № 3 Вычисление и сравнение корней. | Ок 1-4 |
| 4 | П.З. № 4 Решение задач на свойства степени. | Ок 1-4 |
| 5 | П.З. № 5 Степени с рациональными и действительным показателями, их свойства. | Ок 1-4 |
| 6 | П.З№ 6 Решение показательных уравнений и неравенств | Ок 1-4 |
| 7 | П.З. № 7 Нахождение значений логарифмов. | Ок 1-4 |
| 8 | П.З. № 8 Решение задач на свойства логарифмов | Ок 1-4 |
| 9 | П.З. № 9 Решение логарифмических уравнений и неравенств | Ок 1-4 |
| | Раздел 7 ГЕОМЕТРИЯ | |
| | Тема 7.1. Прямые и плоскости в пространстве. | |
| 10 | П.З. № 10 Параллельность прямых и плоскостей. | Ок 1-4 |
| 11 | П.З. № 11 Перпендикулярность прямых и плоскостей. | Ок 1-4 |
| | Раздел 6. Элементы комбинаторики. 12 часов. | |
| | Тема 6.1. Основные понятия комбинаторики | |
| | Раздел 7. ГЕОМЕТРИЯ | |
| | Тема 7.5 Координаты и векторы. | Ок 1-4 |
| 12 | П.З. № 12 Действия над векторами. | Ок 1-4 |
| | Раздел 2 Основы тригонометрии. | Ок 1-4 |
| | Тема 2.1 Основные понятия. | |
| | | |
| | Раздел 2 ОСНОВЫ ТРИГОНОМЕТРИИ | |
| | Тема 2.2. Основные тригонометрические тождества | Ок 1-4 |
| 13 | П.З. № 13 Использование формул приведения для преобразования тригонометрических выражений. | Ок 1-4 |
| 14 | П.З. № 14 Формулы двойного и половинного аргументов. | Ок 1-4 |
| 15 | ПЗ № 15 Формулы суммы и разности для синуса, косинуса, тангенса, двойного аргумента для синуса и косинуса и их применение для преобразования выражений. | Ок 1-4 |
| 16 | ПЗ № 16 Преобразования простейших тригонометрических выражений. | Ок 1-4 |
| | Тема 2.3. Простейшие тригонометрические уравнения и неравенства | |
| 17 | ПЗ № 17 Решение тригонометрических уравнений. | Ок 1-4 |
| 18 | ПЗ № 18 Решение простейших тригонометрических уравнений и неравенств различными способами. | Ок 1-4 |
| | Раздел 3. Функции и графики. | |
| | Тема 3.1. Свойства функции. | |
| 19 | ПЗ № 19 Решение задач методом интервалов | Ок 1-4 |
| 20 | ПЗ № 20 Графическое решение систем неравенств нескольких переменных. | Ок 1-4 |
| | РАЗДЕЛ 7 ГЕОМЕТРИЯ | |
| | ТЕМА 7.2. Многогранники. | |
| 21 | П.З. № 21 Параллелепипед и куб. | Ок 1-4 |
| 22 | П.З. № 22 Пирамида. Правильная пирамида. Усеченная пирамида. Тетраэдр. | Ок 1-4 |
| 23 | П.З. № 23 Построение сечений многогранников. | Ок 1-4 |
| 24 | П.З. № 24 Объем параллелепипеда. Объем призмы. | Ок 1-4 |
| | Тема 7.3. Тела и поверхности вращения | |
| 25 | П.З. № 25 Объемы и поверхности тел вращения. | Ок 1-4 |
| | Раздел 4. Начала математического анализа. | |
| | Тема 4.1. Последовательности. | |
| 26 | П.З. № 26 Предел функции. | Ок 1-4 |
| | Тема 4.2. Производная и её применение | |
| 27 | П.З. № 27 Производная. Понятие о производной функции, ее геометрический и физический смысл. | Ок 1-4 |
| 28 | П.З. № 28 Уравнение касательной к графику функции. Производные суммы, произведения, частного. | Ок 1-4 |
| 29 | П.З. № 29 Нахождение максимума и минимума на отрезке. | Ок 1-4 |
| | Тема 4.3 Интеграл и его применение | |
| 30 | П.З. № 30 Решение интегралов, используя различные методы. | Ок 1-4 |
| 31 | П.З. № 31 Применение формулы Ньютона-Лейбница. | Ок 1-4 |
| 32 | П.З. № 32 Вычисление площадей криволинейных трапеций. | Ок 1-4 |
| | Раздел 6 Элементы теории вероятностей и математической статистики. | |
| | Тема 6.2. Элементы теории вероятностей | |
| 33 | П.З. № 33 Решение задач на сложение и умножение вероятностей. | Ок 1-4 |
| | Раздел 5. Уравнения и неравенства. 20 часов. | |
| | Тема 5.1Уравнения и системы уравнений. Неравенства и системы неравенств с двумя переменными | |
| 34 | П.З. № 34 Основные приемы решения уравнений и неравенств. Способ введения новых переменных. | Ок 1-4 |
| 35 | П.З. № 35 Решение иррациональных уравнений. | Ок 1-4 |
| 36 | П.З. № 36 Решение иррациональных неравенств. | Ок 1-4 |
| | | |
| | Итого за год 36 часов | |
Методические рекомендации по выполнению практических работ
Раздел 1. Алгебра.
Тема 1.1. Развитие понятия о числе.
Практическая работа №1.
Выполнение действий над натуральными, целыми, рациональными и действительными числами.
Цель: повторить правила действий над числами.
Натуральные числа - это числа, которые используются при счете: 1, 2, 3... и т.д. Ноль не является натуральным. Натуральные числа принято обозначать символом N. Два числа отличающиеся друг от друга только знаком, называются противоположными, например, +1 и -1, +5 и -5. Знак "+" обычно не пишут, но предполагают, что перед числом стоит "+". Такие числа называются положительными. Числа, перед которыми стоит знак "-", называются отрицательными. Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.
Рациональные числа - это конечные дроби и бесконечные периодические дроби . Например,
Множество иррациональных чисел обозначается J. Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел. Действительные числа обозначаются символом R.
Задания к практической работе.
Вариант 1
-
Вычислить:
а)3
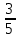 ∙
∙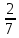 + 1
+ 1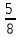 ∙
∙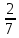 ; б) (
; б) (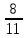 -
- ) ∙ 44 ; в) ( 2
) ∙ 44 ; в) ( 2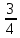 + 4
+ 4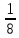
) ∙ 1
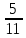 ; г) 6
; г) 6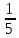 ∙ 4.
∙ 4.-
Упростить выражение и найти его значение при а =
а)
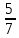 а +
а +  а .
а .-
Докажите, что значение выражения 4,8 +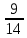 х - 0,5х -
х - 0,5х - 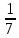 х не зависит от значения х.
х не зависит от значения х. -
Найдите значение выражения:
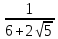 +
+ 
-
Расположите в порядке возрастания числа: 1,5;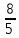 ;
;  ;
; 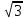 ;
; 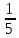 .
.
Вариант 2
1. Вычислить:
а) 9
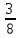 ∙ 2
∙ 2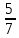 - 2
- 2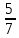 ∙ 7
∙ 7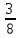 ; б) (
; б) (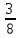 +
+  ) ∙ 24 ; в) 1
) ∙ 24 ; в) 1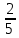 ∙ (1
∙ (1 -
- 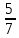 ) ; г)8
) ; г)8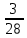 ∙ 5.
∙ 5.2. Упростить выражение и найти его значение при а = 4
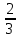
а)
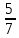 а +
а +  а .
а .3 .Докажите, что значение выражения 4,8 +
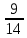 х - 0,5х -
х - 0,5х -