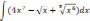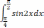Файл: Методические рекомендации для обучающихся к выполнению практических работ по учебной дисциплине.docx
Добавлен: 12.01.2024
Просмотров: 190
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическая работа № 28.
Уравнение касательной к графику функции. Производные суммы, произведения, частного.
Цель: закрепление знаний, отработка навыков вычисления производных.
Задания к практической работе.
| 1 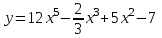 .1 .1 | 1 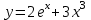 .6 .6 | 1 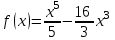 .11 .11 |
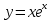 1.2 1.2 | 1 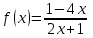 .7 .7 | 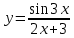 1.12 1.12 |
| 1 | 1 | 1 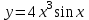 .13 .13 |
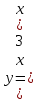 1.4 1.4 | 1.9 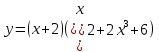 | 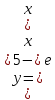 1.14 1.14 |
| 1 | 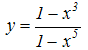 1.10 | 1 |
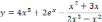 | 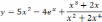 | 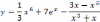 |
Критерии оценки:
«5» ставится за 5 верно решенных заданий;
«4» ставится за 4 верно решенных задания;
«3» ставится за 3 верно решенных задания;
«2» - если решено менее 3 заданий.
Литература.
Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.
Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.
Тема 6.2. Производная и её применение.
Практическая работа № 29.
Нахождение максимума и минимума на отрезке.
Цель: закрепление знаний, отработка навыков исследования функций и построения графиков.
Пояснения к работе: При построении графиков функций с помощью производных придерживаются такого плана:
1) Находят область определения функции и определяют точки разрыва, если они имеются.
2) Выясняют, не является ли функция четной или нечетной; проверяют её на периодичность;
3) Определяют точки пересечения графика функции с координатными осями, если это возможно;
4) Находят критические точки функции;
5) Определяют промежутки монотонности и экстремумы функции.
6) Используя результаты исследования, соединяют полученные точки плавной кривой. Иногда для большей точности графика находят несколько дополнительных точек; их координаты вычисляют, пользуясь уравнением кривой.
Пример. Исследовать функцию и построить график: у =
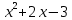
1. Функция определена на интервале
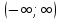 . Точек разрыва нет.
. Точек разрыва нет.2. Функция не является ни четной, ни нечетной, т.к.у
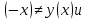 у
у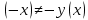 .
. 3. Найдём точки пересечения графика функции с координатными осями. Если у=0, то
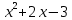 = 0, откуда x = - 1
= 0, откуда x = - 1 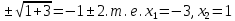 . Значит, кривая пересекает ось абсцисс в точках (-3;0) и (1;0). Если x = 0, то у = - 3, т. е. кривая пересекает ось ординат в точке (0;-3).
. Значит, кривая пересекает ось абсцисс в точках (-3;0) и (1;0). Если x = 0, то у = - 3, т. е. кривая пересекает ось ординат в точке (0;-3). 4. Найдём критические точки функции. Имеем у' = 2x+2, 2x + 2 = 0,
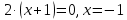 .
.5. Область определения функции разделится на промежутки
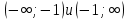 .Знаки производной у′(x) в каждом промежутке можно найти непосредственно подстановкой точки из рассматриваемого промежутка. Так, у′
.Знаки производной у′(x) в каждом промежутке можно найти непосредственно подстановкой точки из рассматриваемого промежутка. Так, у′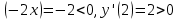 . Следовательно, в промежутке (-∞;-1) функция убывает, а в промежутке (-1;∞) возрастает. При х = - 1 функция имеет минимум, равный у
. Следовательно, в промежутке (-∞;-1) функция убывает, а в промежутке (-1;∞) возрастает. При х = - 1 функция имеет минимум, равный у
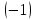 =
= 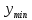 =
= 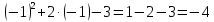 .
. Составим таблицу; строим график.
| х | 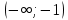 | -1 | 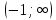 |
| у′  | - | 0 | + |
| у  | 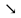 | 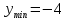 |  |
.
Задания к практической работе.
| Вариант 1 | Вариант 2 |
| 1. Исследуйте функцию и у  = 6х - 2 = 6х - 2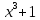 | постройте график. у 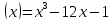 |
| 2. у 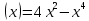 | 2. у 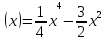 |
| 3.у 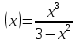 | 3.у 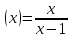 |
Критерии оценки:
«5» ставится за 3 верно решенных заданий;
«4» ставится за 2 верно решенных задания;
«3» ставится за 1 верно решенных задание;
«2» - если решено менее 1 задания
Литература.
Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.
Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.
Тема 6.3 Интеграл и его применение
.
Практическая работа № 30
Решение интегралов, используя различные методы.
-
Цели: Овладеть умением применения первообразной функции при решении вычислительных задач.
Задания к практической работе.
-
Найти неопределённый интеграл, использую таблицу интегралов.
| 1 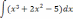 .1 .1 | 1 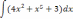 .6 .6 | 1 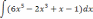 .11 .11 |
| 1 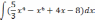 .2 .2 | 1 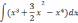 .7 .7 | 1 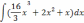 .12 .12 |
| 1 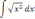 .3 .3 | 1 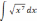 .8 .8 | 1 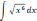 .13 .13 |
| 1 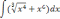 .4 .4 | 1 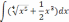 .9 .9 | 1 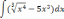 .14 .14 |
| 1 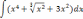 .5 .5 | 1 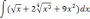 .10 .10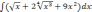 | |
-
Неопределённый интеграл, использую таблицу интегралов.
| 2 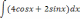 .1 .1 | 2 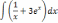 .6 .6 | 2 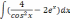 .11 .11 |
| 2 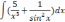 .2 .2 | 2 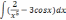 .7 .7 | 2 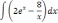 .12 .12 |
| 2 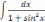 .3 .3 | 2  .8 .8 | 2 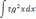 .13 .13 |
| 2 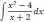 .4 .4 | 2 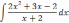 .9 .9 | 2.14 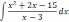 |
| 2 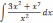 .5 .5 | 2 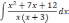 .10 .10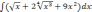 | 2 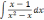 .15 .15 |
-
Найти неопределённый интеграл методом подстановки.
| 3 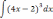 .1 .1 | 3 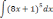 .6 .6 | 3 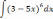 .11 .11 |
| 3 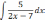 .2 .2 | 3 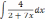 .7 .7 | 3.12 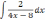 |
| 3 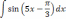 .3 .3 | 3.8 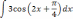 | 3 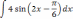 .13 .13 |
Критерии оценки:
«5» ставится за 8-10 верно решенных заданий;
«4» ставится за 6-7 верно решенных заданий;
«3» ставится за 4-5 верно решенных заданий;
«2» - если решено менее 4 заданий
Литература.
Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.
Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.
Тема 6.3 Интеграл и его применение.
Практическая работа № 31
Применение формулы Ньютона-Лейбница.
Цель: закрепление знаний, отработка навыков вычисления площади криволинейной трапеции.
Если f (x) 0 на отрезке [ a, b ], то площадь S соответствующей криволинейной трапеции вычисляется по формуле Ньютона – Лейбница:
Пример. Вычислить площадь фигуры, ограниченной линиями
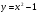 ,
, 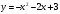 .
.Найдем точки пересечения этих двух линий:
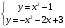
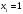 ,
, 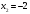
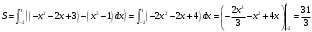 .
.Задания к практической работе.
| Вариант 1 | Вариант 2 | Вариант 3 |
| 1 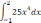 .1 .1 | 1 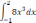 .6 .6 | 1 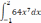 .11 .11 |
| 1.2 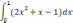 | 1 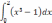 .7 .7 | 1 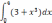 .12 .12 |
| 1 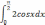 .3 .3 | 1 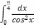 .8 .8 | 1  .13 .13 |
| 1 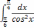 .4 .4 | 1 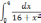 .9 .9 | 1 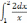 .14 .14 |
| 1 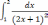 .5 .5 | 1 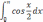 .10 .10 | |