ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 242
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Вариант 2. Усложненный тип балочной клетки
Компоновка и подбор сечения составной главной балки
Изменение сечения балки по длине
Проверка прочности, общей устойчивости и прогиба сварной балки
Проверка местной устойчивости сжатого пояса и стенки сварной балки
Расчет поясного шва сварной балки
fРасчет опорного ребра сварной балки
Момент инерции, приходящийся на поясные листы
I
If тр
I 434250
99251
334999
см4 .
w
Момент инерции поясных листов балки относительно ее нейтральной оси
2
I 2 A
hef
,
f f
2
где Аf – площадь сечения пояса. Моментом инерции поясов относительно их собственной оси ввиду его малости пренебрегаем.
Отсюда получаем требуемую площадь сечения поясов балки:
A
тр 2 If
h
f 2
ef
2 334999
108 2
57 , 44 см2 ,
где hef = h – tf = 110 – 2 = 108 cм.
Принимаем пояса из универсальной стали bf x tf = 300×20 мм Af = 60 см2, для которой отношение
bf / h =300 / 1100=1 / 3,66находится в пределах (1/3 – 1/5) рекомендуемого. Уточняем принятый ранее коэффициент учета пластической работы
«с» исходя из:
f
f
f
A b t 30 2 ,0 60 cм2 ;
w w
w
A h t
106
1,0 106
см2
Af 60
Aw 106
0 ,57
По табл.66 [4] уточняем коэффициент с = 1,11, который практически соответствует ранее принятому значению с = 1,1. Поэтому его оставляем без изменения.
Проверяем принятую ширину (свес) поясов в сечениях, работающих с учѐтом развития пластических деформаций, исходя из их местной устойчивости:
bef
tf
bf t
tf 2
30 1,0
w
2 2
7 , 25
0 ,11
hef
tw
0 ,11
108
1,0
11 ,88 ;
bef
7 , 25
0 ,5
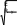 0 ,5
0 ,5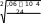 14 ,6 .
14 ,6 .tf
Проверяем несущую способность балки исходя из устойчивости стенки в области пластических деформаций балки в месте действия максимального момента, где
Q и τ = 0.
w 3 ,62 ,
h
w
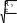
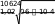 t
t w
2 Af 2
Mmax
208440
кН см
R h t 24 108
y ef C w
Aw
1,0 1,0 0 ,57 0 , 22 221149
кН см,
где α = 0,24 – 0,15·(τ/Rs) – 8,5·10-3( w- 2,2)2 = 0,24-8,5·10-3·(3,62-2,2)2 = 0,22.
Устойчивость стенки балки обеспечена.
Подобранное сечение балки проверяем на прочность. Для этого
определяем момент инерции и момент сопротивление балки
w f
I I I
I 2 b
t( h
/ 2 ) 2
99251
2 30 2 (108
/ 2 ) 2 99251
349920
449171
w f
f ef
cм4 ,
W = ???? ∙ 2 = 449171 ∙ 2 = 8167cm3.


ℎ 110
Наибольшее напряжение в балке:
Mmax
c1W
208440
1,1 8167
23 , 2 кН
cм
cRy
24 кН
cм2 .
Подобранное сечение балки удовлетворяет условию прочности. Высота сечения балки принята больше минимальной, поэтому проверку прогиба балки делать не нужно.
1 2 3 4 5 6 7 8 9 10 11
Изменение сечения балки по длине
Место изменения сечения принимаем на расстоянии 1/6 пролета от опоры. Сечение изменяем уменьшением ширины поясов. Разные сечения поясов соединяем сварным швом встык, электродами Э 42 без применения
физических методов контроля, то есть для растянутого пояса
Rwy
0 ,85
R .
y
Определяем расчетный изгибающий момент и перерезывающую силу в
сечении
х ???? / 6 12 / 6 2 ,0 м.
1
M qх( ???? х) 115 ,8 2 ,0 (12 2 ,0 ) 1158
2 2
кН м 115800
кН см;
Q1 q???? / 2 x 115
,8 12
/ 2 2 ,0 463 , 2 кН.
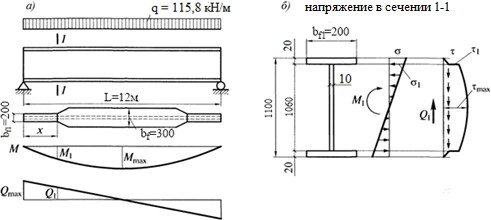
Рисунок 4.4 Изменение сечения
а–место изменения сечения; б–проверка приведѐнных напряжений
Подбор изменѐнного сечения ведем по упругой стадии работы стали. Определяем требуемый момент сопротивления и момент инерции измененного сечения исходя из прочности сварного стыкового шва, работающего на растяжение:
W
тр M1
1
115800
5676
,5 см3 ;
Rwy
0 ,85 24
I
1
1
тр W
h/ 2 5676
,5 110
/ 2 312207
,5 см4 .
Определяем требуемый момент инерции поясов
w
I 99251
см4 ,
тр тр
I
I
1
f1
I 312207
,5 99251
212956
,5 см4 .
w
Требуемая площадь сечения поясов
f1
A
тр
2 Iтр
h
f1 2
ef
2 212956
108 2
,5 36 ,52 см2 .
Принимаем пояс bf1 x tf = 200×20 мм Af1 = 40 см2. Принятое сечение пояса удовлетворяет рекомендациям bf1˃18 см и bf1˃h/10 = 110/10 =11 см.
Определяем момент инерции и момент сопротивления уменьшенного сечения:
hef
1 w f1 f
I I 2 b t
2
99251
2 20 2 108
2
332531
см4 ;
2
2
2 I
1
W
R
h
2 332531
1
110
6046
см4 ;
M1
W1
115800
6046
19 ,15
wy
0 ,85 24
20 , 4 кН
/ см2 .
1 2 3 4 5 6 7 8 9 10 11