Файл: Курсовая работа по дисциплине Ситуационный анализ и моделирование управленческих решений.docx

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ «ВИТЕБСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ П.М. МАШЕРОВА»

Факультет математики и информационных технологий

Кафедра информационных технологий и управления бизнесом

КУРСОВАЯ РАБОТА

по дисциплине «Ситуационный анализ и моделирование управленческих решений»
ЗАДАЧА О НАЗНАЧЕНИЯХ. ВЕНГЕРСКИЙ МЕТОД

Дуброва Никита Николаевич

3 курс, 33 группа

Руководитель:

Кавитова Татьяна Валерьевна

ст. преподаватель кафедры математики, кандидат физ.-математ. наук
Витебск, 2022

Содержание

Введение

Алгоритм под названием “венгерский” был разработан Гарольдом Куном в 1955 году. Кун дал такое название основываясь на том, что этот алгоритм в значительной степени является трудами венгерских математиков Денеша Кёнига (Dénes Kőnig) и Эйгена Эгервари (Jenő Egerváry).

Чуть позже, в 1957 году, Джеймс Манкерс (James Munkres) доказал, что венгерский алгоритм работает за полиномиальное время (т.е. за время порядка полинома, и не зависит от величины стоимостей).

Основываясь на этом алгоритм стали называть не только “венгерским”, но и “алгоритмом Куна-Манкреса” (“алгоритмом Манкреса”).

Однако, в 2006 году было выявлено, что этот алгоритм был изобретён веком ранее, немецким математиком Карлом Густавом Якоби (Carl Gustav Jacobi). Всё дело в том, что напечатанная посмертно, в 1890 году, работа была написана на латыни и была не замечена математиками.

Цель работы:

Исследовать решение задач о назначениях.

Задачи:

Рассмотреть теоретическую часть задач о назначениях.

Проанализировать Венгерский метод решения задач о назначениях.

1. Основы задач о назначениях в теории

Задача о назначениях является ничем иным как частным случаем классической транспортной задачи и, тем самым, является задачей транспортного типа.

Транспортными задачами называются задачи о наиболее выгодном плане перевозок грузов однородного или взаимозаменяемого продукта из станции отправления (пункта производства), в станции назначения (пункты потребления). Несмотря на название данных задач, они имеют обширное применение не только в сфере транспортных перевозок.

---

Основными аспектами интереса к этим задачам можно назвать следующие причины:

1. Задачи транспортного типа решаются, как и задачи линейного программирования, симплекс-методом. Однако некоторые специфические особенности задач данного класса послужили толчком для разработки более эффективных методов решения. А поскольку на практике данные задачи могут быть весьма объёмными, использование специализированных алгоритмов становится не просто возможностью облегчить труд, но и необходимостью.

2. Зачастую для задач транспортного типа используется граф определённой формы. Такое представление является более естественным и удобным. В некоторых случаях представление в виде графа позволяет преобразовать задачи к транспортным (те, которые не имеют ничего общего с ними) и использовать при их решении вычислительные алгоритмы относящиеся к транспортным.

3. Задачи транспортного типа тесно связаны с детерминированными динамическими задачами исследования операций, в том числе и с многошаговыми задачами принятия решений в условиях определенности, имеющими большое прикладное значение.

Некоторые особенности задач о назначениях позволили разработать венгерский метод, как более эффективный метод их решения.

В современном мире все предприятия стараются минимизировать расходы и тем самым увеличить прибыль. С этим помогают экономико-математические задачи о назначениях. Такой вид задач позволяет разместить одного кандидата на выполнение одной работы таким образом, чтобы затраты на выполнение комплекса работ группой исполнителей стали минимальными. Также задачи о назначениях могут быть модифицированы под определённые обстоятельства: во-первых, иногда такие задачи формируются как задачи максимизации (максимизация дохода при назначениях исполнителей на работу); во-вторых, количество рабочих мест может быть меньше, чем количество штатных рабочих и наоборот, количество рабочих может быть меньше, чем количество рабочих мест; в-третьих, выполнение работы может быть запрещено работнику по какому-либо поводу.

Данная задача в такой постановке относится к классу комбинаторных, решение которых, при больших n, становится фактически невозможным для решения перебором (так как число вариантов назначений составляет n!).

2. Задача о назначениях

---

Задача о назначениях – это задача о самом выигрышном распределении работ между таким же числом исполнителей. При решении этой задачи ищут оптимальное назначение из условия максимума общей производительности, которая равна сумме производительности исполнителей. К задаче о назначении можно отнести множество интерпретаций: распределение работников на предприятии в соответствии их работоспособности и навыкам, распределение работы различных механизмов и их энергозатрат и т.д. Венгерский метод является наиболее подходящим для решения данных задач.

3. Венгерский метод решения задач о назначениях

Специфические особенности задач о назначениях послужили поводом к появлению эффективного венгерского метода их решения. Основная идея венгерского метода заключается в переходе от исходной квадратной матрицы стоимости С к эквивалентной ей матрице Сэ с неотрицательными элементами и системой n независимых нулей, из которых никакие два не принадлежат одной и той же строке или одному и тому же столбцу.

Структура алгоритма такова: есть последовательные шаги, на каждом из которых делается попытка выбрать назначение при неотрицательной матрице убытков так, чтобы все выбранные элементы матрицы были нулевыми. Если это сделать не удается, матрица изменяется с сохранением свойства неотрицательности. Первоначально подготовка матрицы заключается в том, что от каждого элемента каждой строки матрицы в каждой строке. Вычитание из каждого столбца наименьшего в нем элемента обеспечивает существование нулевых элементов и в столбцах. Для заданного n существует n! допустимых решений. Если в матрице назначения X расположить n единиц так, что в каждой строке и столбце находится только по одной единице, расставленных в соответствии с расположенными n независимыми нулями эквивалентной матрицы стоимости Сэ, то получим допустимые решения задачи о назначениях.

Следует иметь в виду, что для любого недопустимого назначения соответствующая ему стоимость условно полагается равной достаточно большому числу М в задачах на минимум. Если исходная матрица не является квадратной, то следует ввести дополнительно необходимое количество строк или столбцов, а их элементам присвоить значения, определяемые условиями задачи, возможно после редукции, а доминирующие альтернативы дорогие или дешевые исключить.

---

4. Сущность и решение венгерским методом

Сущность Венгерского метода заключается в продолжении процесса приведения матрицы до тех пор, пока все подлежащие распределению единицы не попадут в клетки с нулевой стоимостью. Это означает, что итоговое значение приведенной целевой функции будет равно нулю. Так как существует ограничение на неотрицательность переменных, нулевое значение целевой функции является оптимальным.

Приведем пример: имеется определенное число работников и определенное число мест. На каждом месте работник имеет определенную заработную плату. Расставить оптимально работников так, чтобы заработная плата была меньше всего. Будем рассматривать с точки зрения руководителя. Работа будет производиться на минимум. В каждой строчке матрицы мы будем выбирать по одному элементу, нельзя чтобы работник работал сразу на двух местах. На каждой строчке и на каждом столбце должно быть по одному выделенному элементу. Распишем сущность алгоритма венгерским методом. Имеем исходную матрицу:

1	7	1	3
1	6	4	6
17	1	5	1
1	6	10	4

Таблица 4.1 – Исходная матрица

Нам нужно вычесть самое маленькое значение из первой строчки. И так далее, вычитаем из каждой строчки до тех пор, чтобы в каждой строчке было хотя бы по одному нулю. Можно и более.

Понижаем порядок матрицы на один.

0	6	0	2
0	5	3	5
16	0	4	0
0	5	9	3

Таблица 4.2 – Исходная матрица с пониженным порядком

Каждый ноль соответствует ребру двудольного графа, напомню, что двудольный граф – это граф, который распадается на два множества, внутри они не соединяются, а соединяются только друг с другом. От I к j вершине. Итак, вершины распадаются на два множества. Первый 0 на месте (1.1) первая вершина соединяется с первой.

---

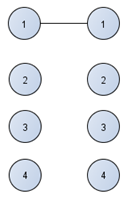
Рисунок 4.1– Соединение первой вершины правой доли двудольного графа



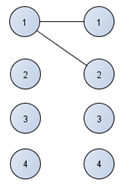
Рисунок 4.2– Второе соединение первой вершины правой доли двудольного графа

Первая с третьим.

Переходим к второй вершине первой доли.


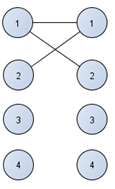
Рисунок 4.3– Соединение второй вершины правой доли двудольного графа

Третья вершина соединяется в двух местах.


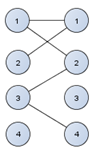
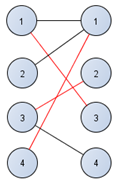
Рисунок 4.4– Соединение третьей вершины правой доли двудольного графа

И последняя соединяется только с первой.


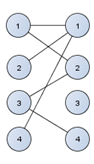
Рисунок 4.5– Соединение четвёртой вершины правой доли двудольного графа

Получился двудольный граф. В нем мы будем искать паросочетания. Паросочетания - это тоже двудольный граф, особенность у него в том, что все степени вершин будут равны единице-это означает что от одной вершины два ребра не пойдет.

Сначала берем любое, затем максимальное и только затем из максимального находим наибольшее. Так находим наибольшее паросочетания. Мы взяли максимальное паросочетание, теперь нам нужно проверить является ли оно наибольшим.



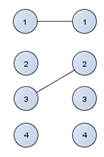
Рисунок 4.6– Первая итерация поиска максимального паросочетания

На отдельном графике найдем наибольшие паросочетания. Если мы будем программировать на компьютере, то он перебирает все возможные варианты. И будет выводить первый попавшийся.

Если есть чередующаяся цепь, то эта чередующаяся цепь состоит из множества X, Y. Состоит из толстых и тонких линий. Тонкие ребра - это все паросочетания полученные из матрицы. Толстые входят в максимальное паросочетание. Из Х прийти в Y по тонким из Y в Х и снова из Х в Y. Потом мы обращаем эту цепь и получаем все наоборот. Из 3 в 2 мы оставим как есть. И добавим тонкие ребра, чтобы посмотреть, есть ли еще чередующаяся цепь.

---