Файл: Курсовая работа по дисциплине Ситуационный анализ и моделирование управленческих решений.docx

Рисунок 4.7–Вторая итерация поиска максимального паросочетания

Есть подозрение, что это максимальное паросочетание.

Но это не единственное максимальное паросочетание. Посмотрим еще один вариант.


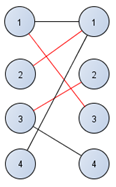
Рисунок 4.8– Третья итерация поиска максимального паросочетания

Это паросочетание тоже является наибольшим. По черным вперед по красным назад. Их количество должно быть нечетным.

Обозначим вершины, которые не охватываются наибольшим паросочетанием.

Xm=	{X4}
Ym=	{Y4}

Таблица 4.3 – Вершины, не охватываемые наибольшим паросочетанием

По этим множествам создадим еще 2 множества: X’ и Y’.

Возьмем Xm и X. Нужно выйти из Xm и вернуться в X. Исходя из той же стратегии: движемся вперед по черным вперед, назад по красным. И смотрим какие при этом мы проходим вершины. Те которые мы проходим вершины помещаем в множества X’ Y’. Выходим из X4 в Y1, затем попадаем в X2.

Получаем:

X'=	{x4, x2}
Y'=	{y1}

Таблица 4.4 – Обратный ход поиска вершин, не охватываемых наибольшим паросочетанием

Теперь по этим номерам строим так называемое альфа-преобразование. Из преобразованной матрицы берем вторую и четвертую строчки и не первый столбец. Из множества Y мы вычитаем Y’: Ym/{Y'}

Выделяем в преобразованной матрице строку 2 и 4, и столбцы все, кроме первой. Нас интересует то, что находится в пересечении.

Мы получили шесть элементов.

0	6	0	2
0	5	3	5
16	0	4	0
0	5	9	3

Таблица 4.5 – Исходная матрица с пониженным порядком

И в этих шести элементах находим минимальное значение. В данном случае получили 3. Далее из этих строк вычитаем тройки и вставляем их в первый столбец. Таким образом, получается:

3	6	0	2
0	2	0	2
19	0	4	0
0	2	6	0

---

Таблица 4.6 – Вычитание из матрицы с пониженным порядком

По аналогии строим граф.


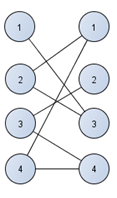
Рисунок 4.9– Построение графа по матрице после вычитания

В этом двудольном графе ищем вариант, который соответствует максимальному значению. Возьмем первую вершину и исследуем её. Проводим от X1 к Y3. От X2 к Y1. От X3 к Y2. Смотрим на то, чтобы не были заняты вершины графа. ОТ X4 к Y4.



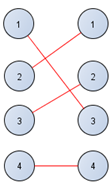
Рисунок 4.10– Граф с совершенным паросочетанием

Получилось совершенное паросочетание. Все степени вершин имеют по единице. Возвращаемся в исходную матрицу.

1	7	1	3
1	6	4	6
17	1	5	1
1	6	10	4

Таблица 4.7– Исходная матрица

Вычисляем сумму выделенных элементов:
1+1+1+4=7
Это и есть ответ решения задачи о назначениях венгерским методом.

5. Реализация задачи о назначениях

Общая структура алгоритма такова: он состоит из последовательных шагов, на каждом из которых делается попытка выбрать назначение при неотрицательной матрице убытков так, чтобы все выбранные элементы матрицы были нулевыми. Если это сделать не удается, матрица изменяется с сохранением свойства неотрицательности.

При неотрицательной матрице значение целевой функции задачи должно быть неотрицательно, поэтому если удастся получить "нулевое" назначение, о котором сказано выше, оно, очевидно, будет оптимальным. Для получения "нулевого" назначения нужно таким образом изменить матрицу, чтобы минимальное значение целевой функции равнялось нулю. Таким образом, невозможность получить "нулевое" назначение показывает, что матрица еще недостаточно изменена.

Метод изменения матрицы очень прост — он состоит из прибавления ко всем элементам какой-либо строки или столбца матрицы одного и того же числа. Поскольку в любом допустимом решении должен быть ровно один элемент из этой строки (или этого столбца), к значению целевой функции при этом изменении прибавляется то же число.

---

Первоначальная подготовка матрицы заключается в том, что от каждого элемента каждой строки матрицы вычитается наименьший в этой строке элемент Матрица становится неотрицательной с нулевым элементом в каждой строке. Вычитание из каждого столбца наименьшего в нем элемента обеспечивает существование нулевых элементов и в столбцах.

Основной шаг алгоритма состоит из поиска "нулевого" назначения и преобразования матрицы. Для "нулевого" назначения лучше воспользоваться терминологией простых графов, считать, что Мх — множество строк матрицы, М2 — множество столбцов и дуга из i в j идет в том и только в том случае, если a[i, j] = 0. Тогда существование "нулевого" назначения эквивалентно существованию в этом графе полного паросочетания. Будем разыскивать в нашем графе максимальное паросочетание (дающее наибольшее число "независимых" нулей - нулей, расположенных в различных строках и столбцах матрицы). Число дуг в максимальном паросочетании равно наименьшему числу вершин в множестве, которому инцидентны все дуги графа. В терминах теорема звучит следующим образом: наибольшее число независимых нулей равно наименьшему числу вертикальных и горизонтальных линий (столбцов и строк), которыми можно перечеркнуть все нули матрицы.

В данной реализации представлен поиск максимального паросочетания в двудольном графе.

Будем рассчитывать из вводимых данных: рабочие, количество назначаемых задания, количество пар (рабочий-задание).

А в выводе отображается количество заданий, заданных по такой схеме.

Заключение

Основной принцип работы венгерского метода состоит в следующем: прибавлением определенным образом найденных чисел к некоторым столбцам и вычитания из них некоторых чисел находят систему так именуемых независимых нулей. Набор из нулей называется системой независимых нулей, если никакие два (или больше) нуля не лежат на одной линии (в строке или столбце). Если число независимых нулей равно n, то, приняв соответствующие им переменные xij равными 1, а все остальные – равными 0, тогда получим оптимальный план назначения.

Алгоритм венгерского метода состоит из предварительного шага и не более чем (n-2) последовательно повторяющихся итераций. На предварительном этапе в случае решения задачи на максимум, ее преобразуют в эквивалентную задачу на минимум. На этом же этапе выделяется система независимых нулей. Каждая последующая итерация направлена на увеличение хотя бы на 1 числа независимых нулей. Как только число независимых нулей k станет равным размерности матрицы (k=n), задача решена. Оптимальный план назначения определится положением независимых нулей на последней итерации.

---

задача назначение венгерский полином

Список используемой литературы

1. Асанов М.О., Баранский В.А., Расин В.В. – Дискретная математика: Графы, матроиды, алгоритмы: Учебное пособие.

2. И.В. Романовский – Алгоритмы решения экстремальных задач.

3. Е.С. Вентцель – Исследование операций: задачи, принципы, методология.


ПРИЛОЖЕНИЕ А

Листинг A –Реализация венгерского алгоритма на языке программирования Pyton
import itertools
import numpy as np
from numpy import random
from scipy.optimize import linear_sum_assignment


# Назначение задачи
class TaskAssignment:

# Инициализация класса, обязательными входными параметрами являются матрица задач и метод распределения, среди которых есть два метода распределения, метод all_permutation или метод Венгрии.
def __init__(self, matrix, mode):
self.matrix = matrix
self.mode = mode
if mode == 'Vengr':
self.min_cost, self.best_solution = self.Vengr(matrix)


def Vengr(self, matrix):
b = matrix.copy()
# Строка и столбец минус 0
for i in range(len(b)):
row_min = np.min(b[i])
for j in range(len(b[i])):
b[i][j] -= row_min
for i in range(len(b[0])):
col_min = np.min(b[:, i])
for j in range(len(b)):
b[j][i] -= col_min
line_count = 0
# Когда количество строк меньше длины матрицы, цикл
while (line_count < len(b)):
line_count = 0
row_zero_count = []
col_zero_count = []
for i in range(len(b)):
row_zero_count.append(np.sum(b[i] == 0))
for i in range(len(b[0])):
col_zero_count.append((np.sum(b[:, i] == 0)))

line_order = []
row_or_col = []
for i in range(len(b[0]), 0, -1):
while (i in row_zero_count):
line_order.append(row_zero_count.index(i))
row_or_col.append(0)
row_zero_count[row_zero_count.index(i)] = 0
while (i in col_zero_count):
line_order.append(col_zero_count.index(i))
row_or_col.append(1)
col_zero_count[col_zero_count.index(i)] = 0
# Нарисуйте линию, покрывающую 0, и получите матрицу после строки минус минимальное значение и столбец плюс минимальное значение
delete_count_of_row = []
delete_count_of_rol = []
row_and_col = [i for i in range(len(b))]
for i in range(len(line_order)):
if row_or_col[i] == 0:
delete_count_of_row.append(line_order[i])
else:
delete_count_of_rol.append(line_order[i])
c = np.delete(b, delete_count_of_row, axis=0)
c = np.delete(c, delete_count_of_rol, axis=1)
line_count = len(delete_count_of_row) + len(delete_count_of_rol)
# Когда количество строк равно длине матрицы, выскакиваем
if line_count == len(b):
break
# Определяем, нужно ли рисовать линию, чтобы покрыть все нули, если она покрывает, операции сложения и вычитания
if 0 not in c:
row_sub = list(set(row_and_col) - set(delete_count_of_row))
min_value = np.min(c)
for i in row_sub:
b[i] = b[i] - min_value
for i in delete_count_of_rol:
b[:, i] = b[:, i] + min_value
break
row_ind, col_ind = linear_sum_assignment(b)
min_cost = matrix[row_ind, col_ind].sum()
best_solution = list(matrix[row_ind, col_ind])
return min_cost, best_solution


# Сгенерировать матрицу затрат
#rd = random.RandomState(10000) # Для случайных значений
#matrix = rd.randint(0, 100, size=(5, 5))
matrix =np.array([[1,7,1,3],[1,6,4,6],[17,1,5,1],[1,6,10,4]])

---

# Используйте метод Венгрии для распределения задач
ass_by_Hun = TaskAssignment(matrix, 'Vengr')
print('cost matrix = ', '\n', matrix)
print('Назначение задачи по венгерскому методу:')
print('min cost = ', ass_by_Hun.min_cost)
print('best solution = ', ass_by_Hun.best_solution)

---