Файл: Контроль обучения 4 Первое контрольное задание 5 Второе контрольное задание 31.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 140
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
else writeln('Сумма отрицательных чисел sum= ', sum);
end.
7. Вводится последовательность из N целых чисел. Найти наибольшее число.
Переменные:
n – количество чисел;
x – очередное число;
i – переменная цикла;
max – наибольшее число.
Алгоритм решения задачи:
-
вводим длину последовательности n и устанавливаем начальное значение max по первому числу; -
последовательно считываем числа и, если очередное число x больше max, то изменяем значение max := x; -
выводим результат.
var n, x, max, i : integer;
begin
repeat
write('Введите длину последовательности n=');
readln(n);
until n>0;
write('Введите x=');
readln(x);
max:=x;
for i:=2 to n do
begin
write('Введите x=');
readln(x);
if (x>max) then max:=x;
end;
writeln('Наибольшее из чисел max=', max);
end.
8. Вводится последовательность целых чисел, 0 – конец последовательности. Найти два наименьших числа.
Переменные:
x – очередное число;
min1 – первое наименьшее число;
min2 – второе наименьшее число (min2>=min1).
Алгоритм решения задачи:
-
устанавливаем начальные значения min1 и min2 по двум первым числам; -
последовательно считываем числа и, если очередное число x меньше или равно min1 (min1 -
если x попадает в интервал от min1 до min2, то изменяем только min2; -
выводим результат.
var x,min1,min2:integer;
begin
write('Введите x=');
readln(x);
min1:=x;
write('Введите x=');
readln(x);
min2:=x ;
{min1<=min2}
repeat
if x<=min1 then
begin
min2:=min1;
min1:=x;
end
else if (min1
write('Введите x=');
readln(x);
until (x=0);
writeln( 'Два наименьших числа равны', min1, 'и', min2);
end.
9. Вводится последовательность ненулевых чисел, 0 – конец последовательности. Определить, является ли последовательность возрастающей.
Переменные:
old – предыдущее число;
new – рассматриваемое число;
f – флаг.
Решение данной задачи строится от противного. Математически для того, чтобы последовательность была возрастающей, для каждого очередного элемента new и предыдущего old должно выполнятся условие new > old. Любое нарушение данного условия приводит к тому, что последовательность не может быть возрастающей.
Алгоритм решения задачи:
-
вводим два первых числа как old и new, задаем начальное значение флага f; -
в цикле ищем нарушение свойства членов возрастающей последовательности; -
переприсваиваем значение old:=new и вводим новое – new; -
в зависимости от флага выводим результат.
var old, new : real;
f : boolean;
begin
write('Введите x=');
readln(old);
write('Введите x=');
readln(new);
f:=true;
repeat
if new<=old then f:=false;
old:=new;
write('Введите x=');
readln(new);
until new=0;
if f then writeln( 'Последовательность возрастающая')
else writeln( 'Последовательность не является возрастающей');
end.
10. Даны натуральное n и последовательность вещественных чисел a1, a2,…, an. Сколько отрицательных чисел в начале последовательности (до первого неотрицательного)?
Переменные:
k – счетчик;
i – переменная цикла;
n – количество членов последовательности;
a – очередной член последовательности;
p – признак отрицательного числа в начале последовательности.
Алгоритм решения задачи:
-
вводим длину последовательности, задаем начальное значение счетчика k; -
устанавливаем признак отрицательного числа p=true; -
в цикле вводим очередной член последовательности; -
если это отрицательное число и до этого неотрицательных чисел не было, то увеличиваем значение счетчика на единицу; -
в противном случае, если член последовательности неотрицателен, то полагаем p=false; -
в зависимости от k выводим результат.
var a: real; p: boolean;
k,n : integer;
begin
repeat
write('Введите длину последовательности n=');
readln(n);
until n>0;
k:=0; p:=true;
for i:=1 to n do
begin
writeln('Введите число');
readln(a);
if (a<0) and p then k:=k+1else
if a>=0 then p :=false
end;
if k=0 then writeln('отрицательных чисел в начале нет')
else writeln('последовательность начинается с ', k, ' чисел')
end.
11. Дан прямоугольный бильярдный стол со сторонами А и В, где А, В – натуральные числа (бильярд Льюиса Кэрролла). Из угловой лузы вылетает шар под углом 45 градусов к боковым стенкам, ударяется о борт, отскакивает, ударяется еще раз и т.д., пока не вылетит через одну из угловых луз. Рассчитать количество отрезков в ломаной траектории шара. Считать угол падения равным углу отражения.
Данная задача решается с помощью стандартных функций выделения целой части от деления y на x (y div x) и выделения остатка y mod x. При прохождении шаром прямоугольного стола и отражении его от боковых сторон происходит увеличение числа отрезков траектории на два, а обратный путь вычисляется как y:=a–x+y mod x, где y – обратный путь для шара, a – длинная сторона стола, x – короткая сторона стола.
Переменные:
а) в функции bill:
x, y – два натуральных числа (формальные параметры);
k – вспомогательная переменная (локальная переменная);
a – длинная сторона стола (глобальная переменная);
б) в основной программе:
a, b – два натуральных числа (глобальные переменные).
Алгоритм решения задачи:
-
создаем описание функции bill; -
вводим два натуральных числа a и b (не кратные друг другу); -
вызываем функцию bill для определения количества отрезков; -
завершаем работу программы.
var a, b : integer;
function bill(y,x:integer):integer;
var k:integer;
begin
k:=0;
while y mod x <>0 do
begin
k:=k+y div x+2;
y:=a–x+y mod x;
end;
bill:=k;
end;
begin
repeat
writeln('Введите два натуральных числа A>B');
readln(a,b);
until a>=b;
writeln('Количество отрезков в траектории :', bill(a,b));
end.
12. Пусть процедура maxmin(x,y) присваивает параметру x большее из вещественных чисел x и y, а параметру y – меньшее. Описать данную процедуру и использовать ее для перераспределения значений вещественных переменных a, b и c так, чтобы стало a>=b>=c.
var a,b,c : real;
procedure maxmin( var x,y:real);
var r:real;
begin if x
writeln('Введите три числа a,b,c –');
readln(a,b,c);
maxmin(a,b);
maxmin(a,c); {a=max}
maxmin(b,c); {c=min}
writeln(a,b,c);
end.
13. Если среди чисел sin(x n) (n = 1, 2, ... ,30) есть хотя бы одно отрицательное число, то логической переменной t присвоить значение true, а иначе – значение false.
var y,x : real;
n : integer;
t : boolean;
begin
write('Введите значение x –');
readln(x);
y:=1; n:=0;
repeat
n:=n+1; y:=x*y; t:=sin(y)<0
until t or (n=30);
writeln(t);
end.
14. Определить k – количество трехзначных натуральных чисел, сумма цифр которых равна n (1
var d1, d2, d3, k, n : integer;
begin
writeln('Введите число n, с которым будем сравнивать сумму цифр числа');
readln(n);
k:=0;
{d1 – левая, d2 – средняя, d3 – правая цифры числа}
for d1:=1 to 9 do
for d2:=0 to 9 do
for d3:=0 to 9 do
if d1+d2+d3=n then begin
k:=k+1; write(d1,d2,d3, ' ');
end;
writeln('Количество искомых чисел равно –', k);
end.
Варианты заданий
| Вариант 1 | Задача 1 Найти знакочередующуюся сумму цифр числа n (пусть запись числа n в десятичной системе есть ak ak – 1 ... a0; найти (–1)k * ak + … + a2 – a1 + a0 ). Вводите число n как значение типа integer. Например, если n = 1234, то ответ равен –1 + +2 – 3 + 4 = 2. Строки не использовать. Подсказка. Как получать цифры целого числа, см. учебное пособие В.М. Зюзьков «Программирование на языке высокого уровня», раздел 2.19. Задача 2 Дана последовательность из n целых чисел. Определите количество чисел в наиболее длинной последовательности из подряд идущих нулей. Например, если n=10 и вводим числа 1, 0, 0, 3, 5, 0, 0, 0, 2, 0, то ответ равен 3. Задача 3 Определить число, получаемое выписыванием в обратном порядке цифр заданного натурального числа n. Вводите число n как значение типа integer. Например, если n = 1234, то ответ равен 4321. Строки не использовать. Подсказка. Как получать цифры целого числа, см. учебное пособие В.М. Зюзьков «Программирование на языке высокого уровня», раздел 2.19. |
| Вариант 2 | Задача 1 Дана последовательность из не менее чем двух натуральных чисел, за которой следует 0. Вычислите сумму тех из них, порядковые номера которых – простые числа. Например, если вводили 1, 12, 8, 4, 50, 6, 77, 8, 9, 0, то номера выделенных чисел являются простыми числами (2, 3, 5, 7) и ответ равен 12 + 8 + 50 + 77 = 147. Подсказка: используйте булевскую функцию для проверки, является номер простым числом или нет. Задача 2 Даны целое n>2 и вещественные числа a1, b1, ..., an, bn (ai < bi). Рассматривая пары ai и bi как левые и правые концы отрезков на одной и той же прямой, определить концы отрезка, являющегося пересечением всех этих отрезков. Если такого отрезка нет, сообщить об этом. Например, если n=3 и a1 = 0, b1= 10, a2 = 1, b2 = 11, a3 = –1, b3 = 5, то результатом будет отрезок [1, 5]. Задача 3 В заданной последовательности чисел длиной n определить длину самой большой упорядоченной по возрастанию подпоследовательности соседних элементов. Например, если вводили 1, 12, 8, 4, 50, 6, 22, 77, 8, 9, 0, то ответ равен 3 (это длина подпоследовательности 6, 22, 77). |
| Вариант 3 | Задача 1 Даны целое n>0 и целые числа a1, a2, ..., an. Определить, сколько чисел последовательности a1, a2, ..., an принимает наибольшее значение. Например, в последовательности 2,5,7,4,7,6,0 наибольшее значение 7 встречается 2 раза. Задача 2 Не используя стандартные функции, вычислить с точностью eps>0 Считать, что требуемая точность достигнута, если очередное слагаемое по модулю меньше eps; все последующие слагаемые можно уже не учитывать. Вложенные циклы не использовать. Подсказка: в двух разных переменных храните отдельно числитель и знаменатель очередного слагаемого и на каждом шаге вычисляйте новые числитель и знаменатель через предыдущие значения. Задача 3 Составьте программу, которая в записи натурального числа N меняет местами крайние цифры, т.е. из 451 получает 154. Вход и выход должны быть значениями типа integer. Подсказка. Как получать цифры целого числа, см. учебное пособие В.М. Зюзьков «Программирование на языке высокого уровня», раздел 2.19. |
| Вариант 4 | Задача 1 Даны натуральные числа n, m. Получить сумму m последних цифр числа n. Число n вводить как величину типа integer и строки не использовать. Пример. Пусть n = 12345, m=3, тогда ответ равен 3+4+5 = =12. Подсказка. Как получать цифры целого числа, учебное пособие В.М. Зюзьков «Программирование на языке высокого уровня», раздел 2.19. Задача 2 Не используя стандартные функции, вычислить с точностью eps>0 Считать, что требуемая точность достигнута, если очередное слагаемое по модулю меньше eps; все последующие слагаемые можно уже не учитывать. Вложенные циклы не использовать. Подсказка: в двух разных переменных храните отдельно числитель и знаменатель очередного слагаемого и на каждом шаге вычисляйте новый числитель через предыдущее значение. Задача 3 Известно, что любое натуральное число N > 7 можно представить в виде N = 3N1 + 5N2 (N1 и N2 0). Напишите программу нахождения всех пар N1 и N2 для числа N. Например, для числа 16 такая пара единственная N1 = 2 и N2 = 2. |
| Вариант 5 | Задача 1 Даны целое n>0 и вещественные числа x1, x2, ..., xn. Определить, сколько из них больше своего предыдущего числа. Задача 2 Не используя стандартные функции, вычислить с точностью eps>0 Считать, что требуемая точность достигнута, если очередное слагаемое по модулю меньше eps; все последующие слагаемые можно уже не учитывать. Вложенные циклы не использовать. Подсказка: в двух разных переменных храните отдельно числитель и знаменатель очередного слагаемого и на каждом шаге вычисляйте новый числитель через предыдущее значение. Задача 3 Определить функцию f(n), значением которой является натуральное число, получаемое выбрасыванием из записи натурального числа n первой справа цифры 0 или 5. Например, f(13510) = 1351, f(1351) = 131. Для данного натурального числа m, примените функцию f последовательно необходимое число раз, так чтобы в записи m не осталось цифр 0 и 5. Подсказка. Как получать цифры целого числа, см. учебное пособие В.М. Зюзьков «Программирование на языке высокого уровня», раздел 2.19. |
| Вариант 6 | Задача 1 Даны натуральное n и вещественные числа x1, y1, x2, y2,…, xn, yn. Рассматривая пары xi, yi как координаты точек на плоскости, определить радиус наименьшего круга (с центром в начале координат), внутрь которого попадают все эти точки. Задача 2 Дано натуральное n>0. Найти произведение первых n простых чисел. Подсказка: используйте булевскую функцию для проверки, является число простым числом или нет. Задача 3 Определите функцию f без параметров, в теле которой вводятся ненулевые целые числа, до тех пор, пока не введется 0. Значением функции является число перемен знаков у членов введенной последовательности (например, в последовательности 1, –34, 8, 14, –5 знак меняется 3 раза). |
| Вариант 7 | Задача 1 Даны целое n>0 и последовательность из n вещественных чисел, среди которых есть хотя бы одно отрицательное число. Найти величину наибольшего среди отрицательных чисел последовательности. Задача 2 var a,b:real; t:boolean; Переменной t присвоить значение true, если уравнения x2 + +6.2x + a2 = 0 и x2 + ax + b – 1 = 0 имеют вещественные корни и при этом оба корня первого уравнения лежат между корнями второго, и присвоить значение false во всех остальных случаях. Задача 3 Даны длины a, b и c сторон некоторого треугольника. Найти медианы треугольника, сторонами которого являются медианы исходного треугольника. Замечание: длина медианы, проведенной к стороне a, равна 0,5 * Определите функцию для вычисления медианы и используете ее необходимое число раз. |
| Вариант 8 | Задача 1 Найти все целые корни уравнения ax3 + bx2 + cx + d = 0, где a, b, c, d – заданные целые числа, причем a<>0 и d<>0. (Замечание: целыми корнями могут быть только положительные и отрицательные делители коэффициента d). Задача 2 Дано: натуральное n, действительные a 1, a 2,...,a n. Вычислить: a1 + a2 * (a2 –1) + a3 * (a3 –1) * (a3 – 2) + a4 * (a4 – 1) * * (a4 – 2) * (a4 – 3) + ... + an * (an – 1) * (an – 2) *...* (an – n +1). Задача 3 Найти все натуральные четырехзначные числа, не превосходящие заданного N, цифры в которых образуют строго возрастающую последовательность (1000 N < 10000). |
| Вариант 9 | Задача 1 Пусть n – натуральное число. Обозначим через n!! произведение 1 * 3 * ... * n для нечетного n и 2 * 4 * 6 * ...* n для четного n. Дано натуральное n. Получить n!!. Задача 2 Даны не менее трех различных натуральных чисел, за которыми следует 0. Определить три наибольших числа среди них (должно выполняться max1 max2 max3). Подсказка. Введите первые три числа в переменные a1, a2 и a3. Присвойте эти значения как начальные для переменных max1, max2, max3, чтобы выполнялось соотношение max1 max2 max3). Затем вводите остальные числа и на каждом шаге осуществляйте необходимую коррекцию max1, max2, max3. Задача 3 С помощью подпрограммы-функции получить значения |
| Вариант 10 | Задача 1 Даны действительные числа x, a, натуральное n. Вычислить: 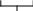 n скобок Задача 2 Дано n вещественных чисел. Найти порядковый номер того из них, которое наиболее близко к квадрату какого-нибудь целого числа. Например, если n=10 и вводим числа 110, 90, 80, 30, 50, 40, 40, 30, 22, 60, то ответ равен 3 или 5 (имеем |80 – 92| = | 50 – 72| = 1). Подсказка: определите функцию f(k), которая вычисляет абсолютную величину разности k и ближайшего целого квадрата (ближайшим целым квадратом будет (trunc( Задача 3 Дано натуральное n. Вычислить: |
| Вариант 11 | Задача 1 Даны натуральное число n, действительные числа x 1 , x 2 , ..., x n (n >= 3). Вычислить: (x1 + 2 * x2 + x3) * (x2 + 2 * x3 + +x4) * ...* (xn – 2 + 2 * xn – 1 + xn). Задача 2 Даны действительные числа x1, y1, x2, y2, x3, y3. Находится ли точка с кординатами (x,y) внутри треугольника с вершинами (x1, y1), (x2, y2), (x3, y3)? Подсказка: соедините точку (x,y) с вершинами треугольника; рассмотрите площади четырех треугольников. Определите функции для вычисления длины отрезка и площади треугольника и используйте эти функции. Задача 3 Вычислить бесконечную сумму с заданной точностью E (E>0). Считать, что требуемая точность достигнута, если вычислена сумма нескольких первых слагаемых и очередное слагаемое оказалось по модулю меньше, чем Е; это и все последующие слагаемые можно уже не учитывать. Вложенные циклы не использовать. Подсказка: вместо вычисления факториала вычисляйте величину, обратную факториалу, тем самым вы избежите целочисленного переполнения (см. учебное пособие В.М. Зюзьков «Программирование на языке высокого уровня», раздел 2.20, задача 3). |
| Вариант 12 | Задача 1 Числа Фибоначчи: F0 = 0, F1 = 1, а любое следующее число Фибоначчи равно сумме двух предыдущих: Fn = Fn – 1 + Fn – 2. Известно, что при достаточно больших n справедливо приближенное равенство Определите наименьший номер n, начиная с которого равенство выполняется с точностью до заданного eps. Задача 2 Вычислить Подсказка: в двух разных переменных храните отдельно числитель и знаменатель очередного слагаемого и на каждом шаге вычисляйте новые числитель и знаменатель через предыдущие значения. Задача 3 День года задан в виде пары целых чисел (m, d), где m – месяц (1m12), d – день (1d31). Программа сначала определяет, правильная ли это дата, и выдает число n, равное 1, 2, …, 6 или 7 в зависимости от того, на какой день недели (понедельник, вторник,…, субботу или воскресение) приходится этот день. Считаем, что год – невисокосный и 1 января – понедельник. |
| Вариант 13 | Задача 1 Рассмотрим последовательность e 1, e 2, e 3,..., образованную по следующему закону e k = Дано действительное eps. Найти первый член e n этой последовательности, для которого |en – en–1| < eps. (Существование en гарантируется одной из теорем математического анализа: чем меньше eps, тем ближе en к числу е = =2,718281828....). Задача 2 Определите, сколько шестизначных чисел чисел имеют одинаковые суммы трех первых и трех последних цифр («счастливые билеты»). Задача 3 Вычислить число , перемножив n сомножителей произведения Валлиса: |
| Вариант 14 | Задача 1 Определите функцию f(n), n – натуральное число, равную сумме цифр числа n. Исследуйте, есть ли среди чисел < m такие n, что (f(n))2 = n. Подсказка. Как получать цифры целого числа, см. учебное пособие В.М. Зюзьков «Программирование на языке высокого уровня», раздел 2.19. Задача 2 Даны натуральные n, m. Получить все меньшие n натуральные числа, сумма цифр которых равна m. Подсказка. Как получать цифры целого числа, см. учебное пособие В.М. Зюзьков «Программирование на языке высокого уровня», раздел 2.19. Задача 3 Вычислить число , учитывая n членов ряда Грегори: |
| Вариант 15 | Задача 1 Дано натуральное n. Вычислить:  n корней Задача 2 Вычислить 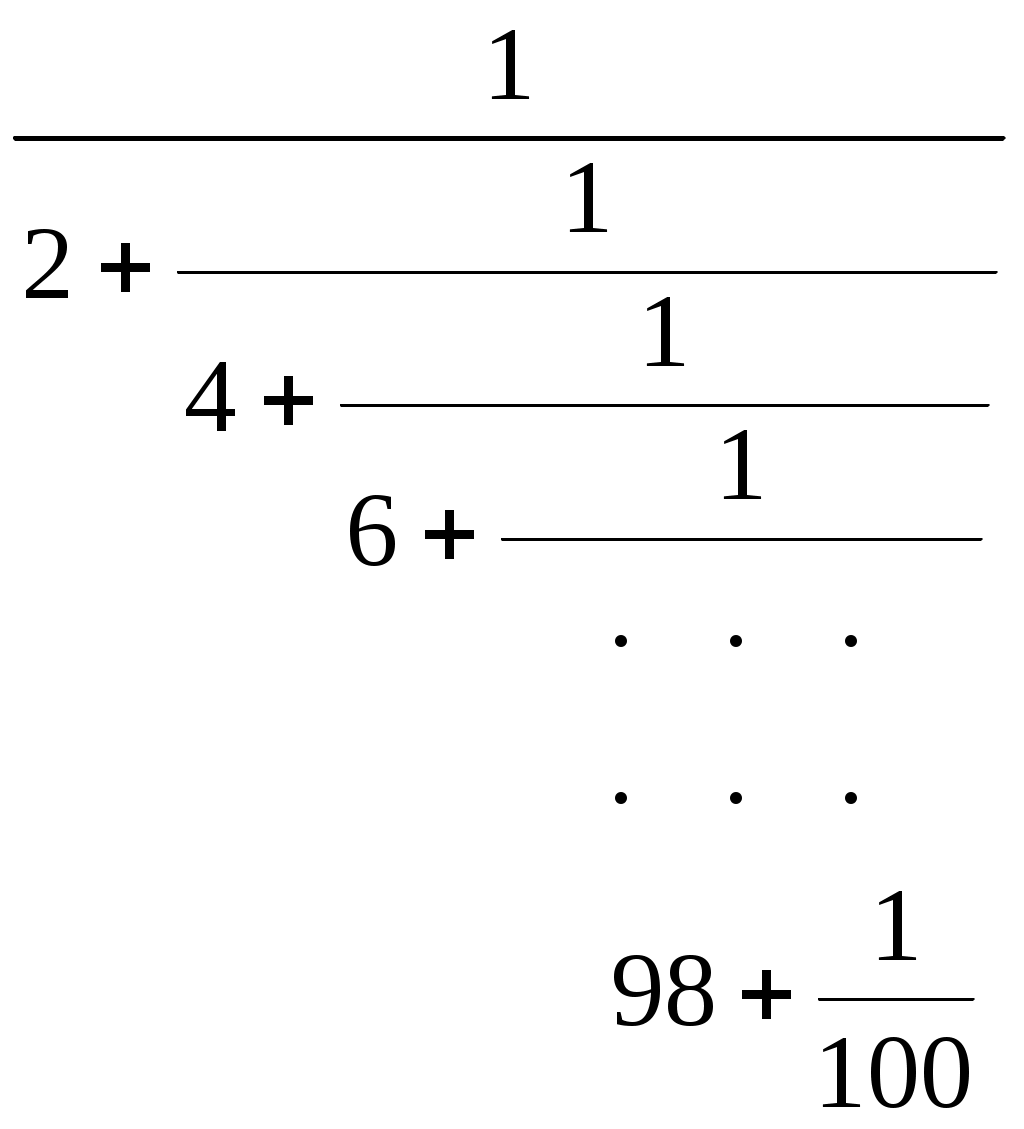 Задача 3 Пусть дано натуральное число n. Составить программу вычисления n3 как суммы нечетных чисел, исходя из того, что: 13=1; 23 = 3+5; 33=7+9+11; 43 = 13+15+17+19; 53 = =21+23+25+27+29; … |
| Вариант 16 | Задача 1 Даны натуральные числа m и n. Найти такие натуральные p и q, не имеющие общих делителей, что p/q = m/n. Задача 2 Даны натуральное n и целые числа c1, c2, … , cn. Имеются ли в последовательности c1, c2, … , cn: а) два идущих подряд нулевых члена; б) три идущих подряд нулевых члена? Задача 3 Вычислить с точностью eps>0 бесконечную сумму Считать, что требуемая точность достигнута, если очередное слагаемое по модулю меньше eps; все последующие слагаемые можно уже не учитывать. |
| Вариант 17 | Задача 1 Даны натуральное число n и целые числа a1, a2,…, an. Найти наибольшее из нечетных чисел и количество четных чисел, входящих в последовательность a1, a1+1, a2, …, an. Задача 2 Даны натуральное число n, действительные числа x1, x2, …, xn, xn+1, …, x2n. Вычислить сумму чисел из xn+1, …, x2n, которые превосходят по величине все числа x1, x2, …, xn. Задача 3 Вычислить с точностью eps>0 бесконечную сумму Считать, что требуемая точность достигнута, если очередное слагаемое по модулю меньше eps; все последующие слагаемые можно уже не учитывать. |
| Вариант 18 | Задача 1 Даны натуральное n и целые числа c1, c2, … , cn. Имеются ли в последовательности c1, c2, … , cn три идущих подряд нулевых члена? Задача 2 Даны натуральное число n и натуральные числа x1, x2, …, xn. Найти номер последнего простого числа в последовательности x1, x2, …, xn; если простых чисел нет, то ответом должно быть число n+1. Подсказка: используйте булевскую функцию для проверки, является число простым числом или нет. Задача 3 Составить программу вычисления значения функции Z(x) = 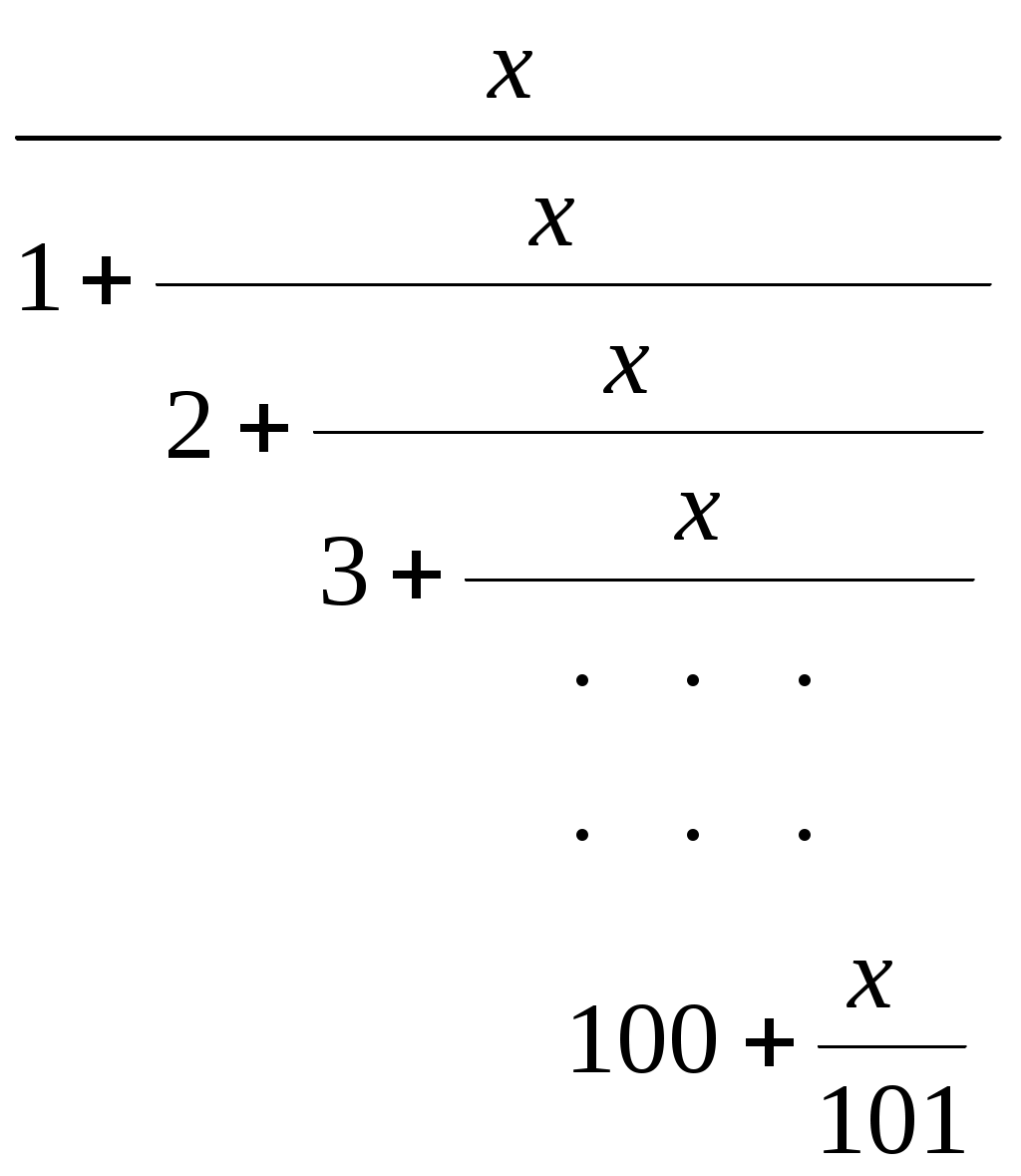 |
| Вариант 19 | Задача 1 Вводим вещественные числа x1, x2, … до тех пор, пока не введем отрицательное число (первое число неотрицательное). И пусть x1, x2, …, xn – члены данной последовательности, предшествующие отрицательному числу. Посчитать количество полных квадратов среди чисел x1, x2, …, xn. Подсказка. Число k является полным квадратом, если выполнено равенство k = (trunc( Задача 2 Даны натуральное число n и действительные числа x1, x2, …, xn. Выяснить, какое число встречается в последовательности x1, x2, …, xn раньше – положительное или отрицательное. Если все члены последовательности равны нулю, то сообщить об этом. Задача 3 Составить программу вычисления значения функции Z(x) = 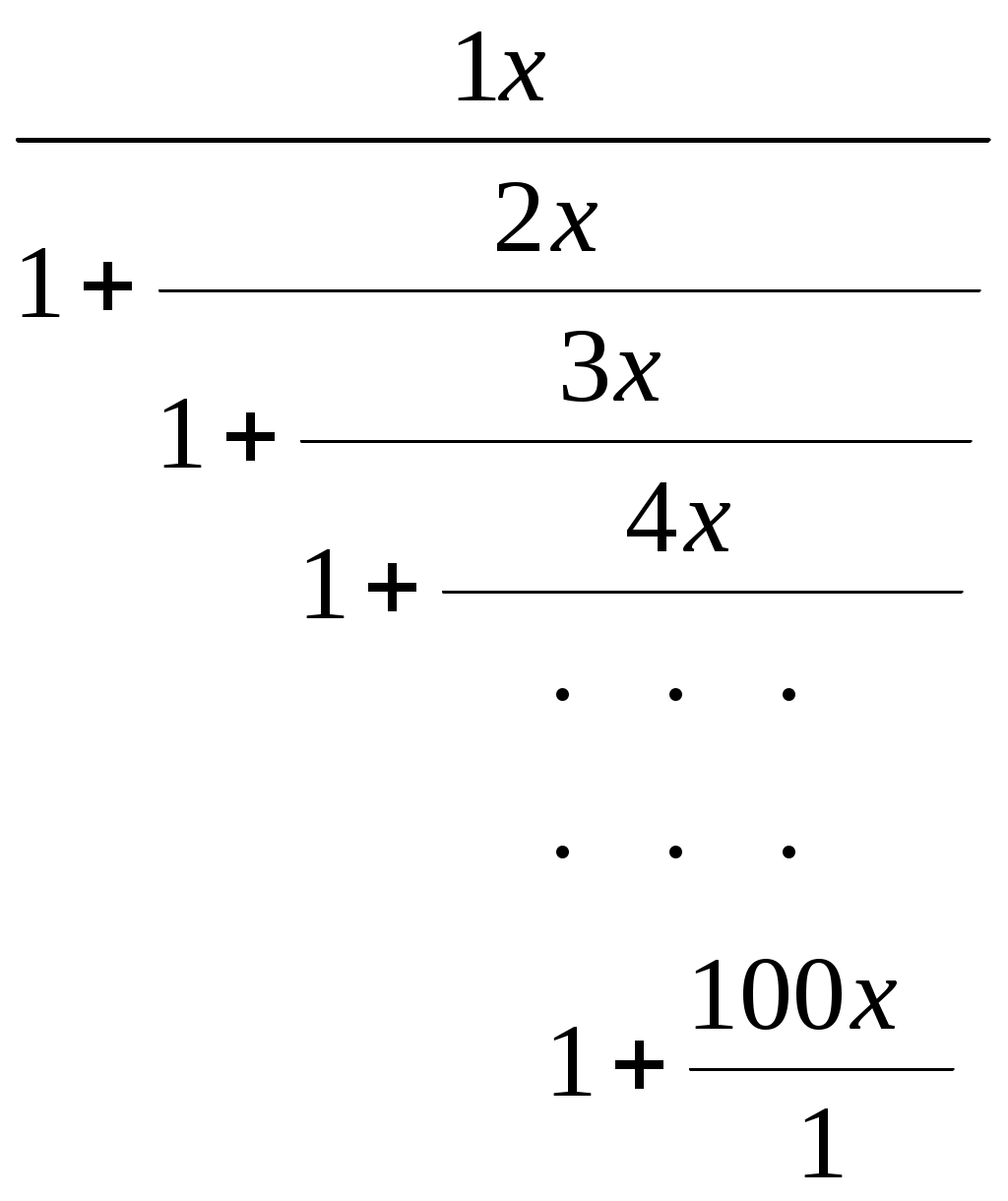 |
| Вариант 20 | Задача 1 Даны натуральное число n, действительные числа x1, x2, …, xn. Найти длину наименьшего отрезка числовой оси, содержащего все числа x1, x2, …, xn. Задача 2 Даны натуральное число n и натуральные (большие 0) числа x1, x2, …, xn. Выяснить, какое число встречается в последовательности x1, x2, …, xn раньше – составное или простое. Если все члены последовательности равны 1, то сообщить об этом. Подсказка: используйте булевскую функцию для проверки, является число простым числом или нет. Задача 3 Д 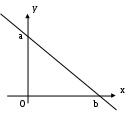 аны вещественные a>0, b>0. Напишите функцию f(a,b), которая считает, сколько точек с целочисленными координатами (x,y) находится в треугольнике. Если точка попадает на сторону треугольника, то она должна тоже учитываться. аны вещественные a>0, b>0. Напишите функцию f(a,b), которая считает, сколько точек с целочисленными координатами (x,y) находится в треугольнике. Если точка попадает на сторону треугольника, то она должна тоже учитываться.Например, f(1,1) = 3. |
0>
1 2 3
Второе контрольное задание
Второе контрольное (текстовое) задание посвящено созданию программ с использованием массивов (одномерных и матриц), переменных строкового типа (строк) и множеств. В этих задачах полезно использовать подпрограммы. Во всех задачах строки вводятся пользователем с клавиатуры.
Задание состоит из четырех задач, вам требуется составить программы на языке Паскаль. Требуется писать программы в рамках структурного программирования. В частности, запрещается использовать операторы перехода и метки.
Примеры задач с решением
ОДНОМЕРНЫЕ МАССИВЫ
1. Дан массив чисел. Найти, сколько в нем пар одинаковых соседних элементов.
Переменные:
mas – массив чисел;
n – размер массива;
i – переменная цикла;
k – количество одинаковых пар соседних элементов.
Алгоритм решения задачи:
-
вводим длину массива n, значение элементов массива и устанавливаем начальное значение k; -
последовательно просматриваем элементы и, если очередной mas[i] равен следующему mas[i+1], то увеличиваем значение k на единицу; -
выводим результат.
const m=100;
var mas : array [1..m] of integer;
i, k, n : integer;
begin
write('Введите размер массива n=');
readln(n);
k:=0;
for i:=1 to n do
begin
write('Введите элемент массива');
readln(mas[i]);
end;
for i:=1 to n–1 do
if mas[i]=mas[i+1] then k:=k+1;
wrietln('Одинаковых пар соседних элементов ',k);
end.
2. Программа. Дано 100 целых чисел. Распечатать их в обратном порядке по 6 чисел в строке.
const n=100; d=6;
var x : array [1..n] of integer;
i, k : integer;
begin
{ввод массива:}
writeln('Введите массив из ', n,' чисел');
for i:=1 to n do read(x[i]);
{вывод массива по d чисел в строке:}
k:=0; {номер числа в строке}
for i:=n downto 1 do
begin
k:=k+1;
write(x[i]:4);
if k=d then
begin
k:=0; writeln
end
end;
if k<>0 then writeln
end.
3. Сортировка слиянием
const k=50; m=20; n=70; {n=k+m}
var x : array [1..k] of real;
y : array [1..m] of real;
z : array [1..n] of real;
i,p,j : integer;
Элементы каждого из массивов x и y упорядочены по неубыванию. Объединить элементы этих двух массивов в один массив z так, чтобы они снова оказались упорядоченными по неубыванию.
const k=50; m=20; n=70; {n=k+m}
var x : array [1..k] of real;
y : array [1..m] of real;
z : array [1..n] of real;
i, p, j : integer;
begin
writeln('Введите массив x');
for i:=1 to k do read(x[i]);
writeln;
writeln('Введите массив y');
for i:=1 to m do read(y[i]);
writeln;
writeln('Введенные Вами массивы');
writeln('Массив x');
for i:=1 to k do write(x[i]:7:3);
writeln;
writeln('Массив y');
for i:=1 to m do write(y[i]:7:3);
writeln;
p:=1; {индекс очередного элемента из z}
i:=1; {из х}
j:=1; {из y}
{пока есть нерассмотренные элементы и в x, и в y: }
repeat if x[i]
begin
z[p]:=x[i]; i:=i+1
end
else
begin
z[p]:=y[j]; j:=j+1
end;
p:=p+1
until (i>k)or(j>m);
{один из массивов x или y исчерпан --> перепись в z
оставшихся элементов другого массива:}
if i>k {исчерпан массив x:}
then repeat z[p]:=y[j]; j:=j+1; p:=p+1 until j>m
else repeat z[p]:=x[i]; i:=i+1; p:=p+1 until i>k;
writeln('Полученный массив: ');
for i:=1 to n do write(z[i]:7:3);
end.
4. type shift=1..99;
scale=array [1..100] of real;
Описать процедуру move(s,k), которая преобразует шкалу s, циклически сдвигая ее элементы на k позиций влево, где k – параметр типа shift.
type shift=1..99;
scale=array [1..100] of real;
var a:scale; m:shift;n,i:integer;
procedure move( var s:scale; k:shift);
var i:integer; t:scale; {вспомогательный массив}
begin
{t[n–k+1..n]:=s[1..k]:}
for i:=1 to k do t[n–k+i]:=s[i];
{t[1..n–k]:=s[k+1..n]:}
for i:=k+1 to n do t[i–k]:=s[i];
s:=t
end;
begin
writeln('Введите размер массива');
readln(n);
writeln('Введите массив');
for i:=1 to n do read(a[i]);
writeln('Введите цикл сдвига <=', n–1);
readln(m);
writeln('Исходный массив');
for i:=1 to n do write(a[i]:7:2);
writeln;
move(a,m);
writeln('Полученный массив');
for i:=1 to n do write(a[i]:7:2);
writeln;
end.
МНОГОМЕРНЫЕ МАССИВЫ
5. Дана матрица NM, состоящая из натуральных чисел. Выбрать в строках самые левые наименьшие элементы и поставить их в первый столбец.
Для решения этой задачи нужно сначала найти самый левый минимальный элемент в каждой строке и запомнить его местоположение, а затем поменять его местами с элементом в первом столбце.
Переменные:
a – двумерный массив;
n, m – количество строк и столбцов массива;
i, j – переменные цикла;
jm – столбец минимального элемента для каждой строки;
min – текущий минимум.
Алгоритм решения задачи:
-
вводим размеры массива А и значения его элементов; -
просматриваем строки массива слева направо, ищем минимальное значение и запоминаем значения индексов; -
для каждой строки меняем местами минимальный элемент и элемент в первом столбце; -
выводим матрицу на экран.
const t=100; s=100;
var a : array [1..t,1..s] of integer;
n, m, jm, i, j, min : integer;
begin
write('Введите количество строк n=');
readln(n);
write('Введите количество столбцов m=');
readln(m);
for i:=1 to n do
begin
write('Введите через пробел', m,'чисел');
for j:=1 to m do
read(a[i,j]);
end;
for i:=1 to n do
begin
min:= a[i,1];