Файл: Контрольная работа По дисциплине Информационные технологии в корпоративных сетях.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 146
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Если целевые функции и допустимые множества участников системы зависят от некоторых параметров, то можно исследовать зависимость структуры системы от этих параметров – при тех комбинациях параметров, при которых имеет место вышеупомянутое условие следует реализовывать матричную структуру, при остальных значениях параметров – линейную структуру. Если известна стоимость изменения этих параметров, то можно ставить решать задачу развития (оптимального изменения параметров с учетом затрат на изменения и эффективности структур) по аналогии с тем, как это делается в [2].
Рассмотрим пример, иллюстрирующий применение описанного общего подхода. Рассмотрим систему, состоящую их одного АЭ и двух центров. Стратегией АЭ является выбор действия
 , содержательно интерпретируемого как доля всего рабочего времени АЭ, отрабатываемого на первый центр. Соответственно, (1 – y) характеризует долю времени, отрабатываемого на второй центр. Центры получают доходы, зависящие от того времени, которое на них отработал АЭ: H1(y) = y, H2(y) = y, где
, содержательно интерпретируемого как доля всего рабочего времени АЭ, отрабатываемого на первый центр. Соответственно, (1 – y) характеризует долю времени, отрабатываемого на второй центр. Центры получают доходы, зависящие от того времени, которое на них отработал АЭ: H1(y) = y, H2(y) = y, где  - некоторый параметр. АЭ несет затраты c(y) = y2 / 2 + (1 – y)2 / 2.
- некоторый параметр. АЭ несет затраты c(y) = y2 / 2 + (1 – y)2 / 2.Определим наиболее выгодное для первого центра действие АЭ (максимизирующее разность между H1(y) и c(y)):

Определим наиболее выгодное для второго центра действие АЭ (максимизирующее разность между H2(y) и c(y)):

Вычисляем соответствующие значения целевых функций центров:
-
в области центры получают (управляя АЭ поодиночке) следующие полезности: W1 = 1 – / 2, W2 = – /2;
центры получают (управляя АЭ поодиночке) следующие полезности: W1 = 1 – / 2, W2 = – /2; -
в области центры получают (управляя АЭ поодиночке) следующие полезности: W1 = - 1 / 2, W2 = [6 – (1 + ) 2 – 2 – 3 + 2 ] / 2 ( – 1)2,
центры получают (управляя АЭ поодиночке) следующие полезности: W1 = - 1 / 2, W2 = [6 – (1 + ) 2 – 2 – 3 + 2 ] / 2 ( – 1)2, -
в области центры получают (управляя АЭ поодиночке) следующие полезности: W1 = - 1 / 2, W2 = - 1 / 2.
центры получают (управляя АЭ поодиночке) следующие полезности: W1 = - 1 / 2, W2 = - 1 / 2.
Определим действие y0, доставляющее максимум [H1(y) + H2(y) – c(y)]: y0 = min [ / (1 + ); 1], и

Условие непустоты области компромисса (и реализуемости матричной структуры) имеет вид:
(15)

Так как каждая из величин W1, W2 и W0 зависит от параметров (; ), то можно найти множество значений этих параметров, при которых условие (15) выполнено. Для рассматриваемого примера на рисунке 16 заштриховано множество значений параметров и , при которых оптимальной является матричная структура. В незаштрихованных областях оптимальна линейная структура, причем в равновесии АЭ оказывается починенным всегда только второму центру.

Рис. 16. Области значений параметров и , в которых оптимальна матричная структура
Параметрический анализ, аналогичный проведенному выше, оказывается эффективным и в динамике, так как знание областей оптимальности различных структур при наличии прогноза изменений существенных параметров позволяет априори синтезировать структуру управляющей компании, обладающую максимальной (или максимальной ожидаемой, или допустимой и т.д. – в зависимости от решаемой задачи) эффективностью.
Тесты к урокам.
Урок 1.
Вопрос 1.
Задача распределения объемов j-ой работы между элементами множества
 имеет вид:
имеет вид:1).
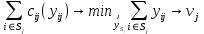 . +
. +2).
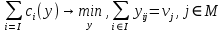 .
.3).
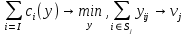 .
.4).
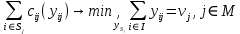
Вопрос 2.
Если
 – функция затрат i-го АЭ, то задача распределения работ может быть сформулирована в виде:
– функция затрат i-го АЭ, то задача распределения работ может быть сформулирована в виде:1).
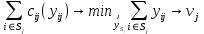
2).
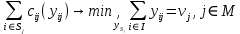
3).
 +
+4).
 .
.Урок 2.
Вопрос 1.
В какую задачу превращается задача распределения объемов j-ой работы между элементами множества
 в частном случае, когда число АЭ равно числу работ, затраты АЭ сепарабельны и удельные затраты cij i-го АЭ по выполнению j-ой работы постоянны,
в частном случае, когда число АЭ равно числу работ, затраты АЭ сепарабельны и удельные затраты cij i-го АЭ по выполнению j-ой работы постоянны, 
1).
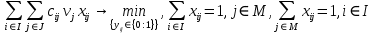 . +
. +2).

3).
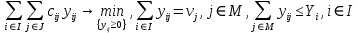 .
.Вопрос 2.
Если задача (4)-(5) является стандартной задачей математического программирования, то задача (6) принадлежит к:
1). задачам дискретной оптимизации +
2). стандартным транспортным задачам
3). стандартным задачам о назначении
Урок 3.
Вопрос 1.
Постановка и решение задач «назначения» позволяет оценивать
1). сравнительную эффективность различных структур и закономерностей их трансформации
2). осуществлять выбор оптимальной или рациональной структуры управляющей компании в зависимости от набора проектов, реализуемых в рамках корпоративной программы
3). Все ответы верны +
Урок 4.
Вопрос 1.
Условие непустоты области компромисса (и реализуемости матричной структуры) имеет вид:
1).
 +
+2).
 .
.3).
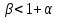
Вопрос 2.
Условием реализации режима сотрудничества является
1). непустота области компромисса +
2). матричная структура
3).
 .
.Заключение
В данной работе была изучена часть 2 параграф 2.4 «Модели и методы оптимизации структуры управляющей компании» из монографии Гламаздина, Е. С. «Управление корпоративными программами». Были составлены уроки по параграфу и созданы тесты по каждому из них.
Работа Гламаздина содержит описание информационного окружения корпоративных систем управления программами (первая часть), а также теоретико-игровые и оптимизационные модели управления корпоративными программами (вторая часть).
1 Под функциональной в общем случае понимается линейная (древовидная) структура, в которой подразделения выделяются по тому или иному признаку (на различных уровнях иерархии признаки могут быть различны): функциональному, территориальному, продуктовому и т.д.
2 Под функциональной в общем случае понимается линейная (древовидная) структура, в которой подразделения выделяются по тому или иному признаку (на различных уровнях иерархии признаки могут быть различны): функциональному, территориальному, продуктовому и т.д.