Файл: Протокол 1 от 28 августа 2020 г. Конспект лекций содержание введение Краткая характеристика дисциплины.doc

На рисунке 6 приведена карта Карно для заданной функции.

Для вертикальной группы простая импликанта равна: .

Эта группа занимает два столбца, в которых аргументы Х1 одинаковые, а Х2разные. Склеивание происходит по аргументу Х2. Так как данная группа занимает все четыре строки, то все аргументы, соответствующие этим строкам, склеиваются.

Горизонтальная группа занимает все четыре столбца, поэтому аргументы Х1 и Х2 склеиваются между собой. В строке данной группы находятся аргументы Х3=1 и Х4=0. Поэтому простая импликанта для этой группы равна: .


00 01 11 10

Х2Х1 Х4Х3

00 01 11 10 00 01 11 10 0	1	3	2
00 01 11 10 4	5	7	6
12	13	15	14
8	9	11	10

1	1	1	0
1	1	1	1
0	1	1	0
1	1	1	0

Х2Х1 Х4Х3

а) шаблон Карты Карно для 4-х аргументов в наборах

б) заполнение карты согласно шаблону

Рисунок 26 - Карта Карно для заданной функции
Для группы, занимаемой крайние соседние клетки, простая импликанта равна: .


П 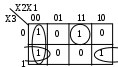ример

---

4: Если в диаграмме или карте Карно присутствует клетка, которую нельзя объединить ни с какой другой клеткой, то она считается одиночной. Ответ для нее записывается в виде минтерма, соответствующего значению данной клетки.

Рисунок 27 – Объединение клеток карты

Минимальная форма такой функции МДФ:

Таким образом, метод Вейча является самым удобным для минимизации логических функций, образованных от небольшого количества аргументов.

1.4.5 Минимизация Неполностью Заданных Логических Функций
Иногда возникает необходимость синтезировать устройства, в которых на его вход некоторые наборы аргументов никогда не подаются. В этом случае значения функций на этих наборах не определены (не заданы). Такие функции называют неполностью заданными, неопределенными.

Чтобы синтезировать такое устройство, необходимо доопределить значения функций на неиспользуемых наборах аргументов. Функции придают значения либо «0» либо «1», при которых можно обеспечить построение наиболее простой схемы. Клетки, соответствующие неиспользуемым наборам аргументов отмечаются звездочкой «*».

Минимизацию неполностью заданной логической функции легче всего осуществить методом Вейча. При объединении клеток диаграммы используют основные правила минимизации функций методом Вейча с учетом клеток, обозначенных звездочкой «*».
Пример 5: Дана функция четырех аргументов, представленная в форме СНДФ.

Ф
1-й набор
7-й набор
14-й набор
10-й набор

ункция не определена на значениях аргументов:
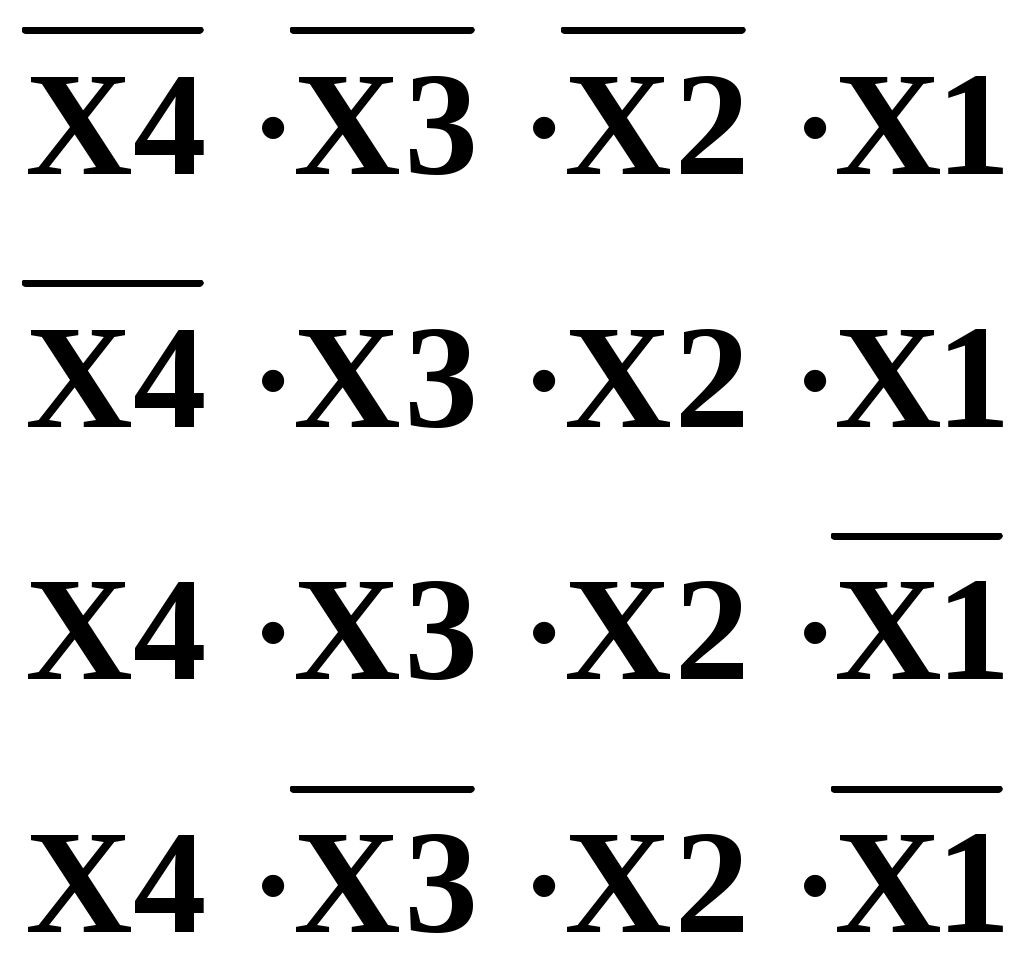
Заполняем диаграмму Вейча в соответствии с заданными значениями наборов (рисунок 8). Оставшиеся незаполненные клетки соответствуют нулевому значению функции.

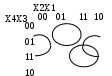
0	*	1	0
1	1	*	1
1	0	1	*
0	0	1	*

---

Рисунок 28—Диаграмма неполностью заданной логической функции

0		1	0
1	1		1
1	0	1
0	0	1

---

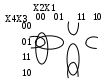
Рисунок 29 –Диаграмма функции СНДФ

В результате минимизации доопределенной функции получим выражение:

Если неиспользуемым наборам аргументов придать значение нуля «0», то диаграмма будет иметь вид, представленный на рисунке 9, а минимальная форма:

При сравнении видно, что минимальная форма доопределенной функции проще, чем минимальная форма неполностью заданной логической функции.

1.4.6 Синтез КЦУ
В процессе проектирования любого устройства приходится выполнять ряд действий, которые могут быть отнесены к задачам анализа и синтеза.

К схемам КЦУ относятся такие устройства, как шифратор, дешифратор, сумматор, преобразователи кодов и другие.

Анализ КЦУ производится по готовой структурной схеме, построенной на логических элементах заданного базиса. В процессе анализа оцениваются некоторые характеристики КЦУ.

Например, запись исходного логического выражения; определение типа логических элементов и экономические затраты на реализацию (т.е. построение) схемы; быстродействие схемы и потребляющую емкость и т.п.

Синтезировать КЦУ, значит построить структурную схему логического устройства по заданному уравнению, т.е. определить тип необходимых логических элементов и соединение между ними с учетом заданной логической функции.

Синтез КЦУ можно выполнить в любом базисе.
1.4.7 СИНТЕЗ КЦУ В БАЗИСЕ И, ИЛИ, НЕ
Для построения схемы в базисе И, ИЛИ, НЕ используются операции:

Инверсия (НЕ)

Конъюнкция (И)

дизъюнкция (ИЛИ)

При построении логической схемы важно определить в какой последовательности следует выполнять действия.

Пример 6: Логическая функция задана в форме НДФ

Произведем анализ логического выражения.

---

Для построения схемы логического устройства необходимо:

1 Выполнить инверсию аргументов Х2 и Х3. Для этого используем два элемента НЕ: ;

2 Выполнить логическое сложение аргументов (т.е. операции в скобках). Для этого используем два элемента ИЛИ на два входа;

3 Выполнить логическое умножение групп аргументов Для этого используем один элемент И на два входа.
Схема логического устройства в базисе И, ИЛИ, НЕ приведена на рисунке 10.
Производим выбор микросхем (смотри ПРИЛОЖЕНИЕ).

При выборе элементов микросхем необходимо ввести их обозначение. Элементы микросхем условно обозначаются двумя буквами DD. Рядом с буквами располагаются две цифры. Первая цифра обозначает порядковый номер выбранной микросхемы, вторая—номер логического элемента в данной микросхеме.

Так логические элементы НЕ схемы (рисунок 10) обозначим DD 1.1, DD1.2 микросхемы К155ЛН1. Она содержит 6 элементов НЕ. Для построения данной схемы используется только 2 элемента из 6, т.е. 2/6 микросхемы.

Логические элементы ИЛИ обозначим в схеме как DD 2.1, DD2.2 и используем микросхему К155ЛЛ1. Она содержит 4 элемента ИЛИ. Для построения данной схемы используется только 2 элемента из 4, т.е. 2/4 микросхемы.

Логические элементы И обозначим DD 3.1 микросхемы К155ЛИ1. Она содержит 4 элемента И. В схеме используется только 1 элемент из 4, т.е. 1/4 микросхемы.

Таким образом, в данной схеме использованы ИМС К155ЛН1-DD1, К155ЛЛ1-DD2, К155ЛИ1-DD3



У=1

Рисунок 30  Логическая схема ЦУ в базисе И, ИЛИ, НЕ
Подаем на входы схемы логические сигналы Х3= 0, Х2=0, Х1=1 и определяем значение сигналов на выходе каждого элемента и значение функции на выходе схемы. Их значение определяется согласно таблицы истинности логических элементов (см. методическую разработку Логические функции одного и двух аргументов).
1.4.8 СИНТЕЗ КЦУ В БАЗИСЕ И—НЕ , ИЛИ-НЕ
Реализация логической функции в базисе И—НЕ либо ИЛИ—НЕ сводится к построению логической схемы с использованием соответствующих элементов:

---