Файл: Построение графиков в Turbo Pascal.doc

Лабораторная работа №1

Составить программу построения графика функции, используя точечный метод. Выбрать произвольно цвет фона, цвет изображения.

1. y=sin(2x+1) на отрезке [-2π, 2π].

2. y=2sin(x) на отрезке [0, 3π].

3. y=sin(3x+1) на отрезке [-π, π].

4. y=3sin(x) на отрезке [-2π, 0].

5. y=sin(1/2x) на отрезке [-2π, 2π].

6. y=cos(2x) на отрезке [-π, π].

7. y=1/2cos(x) на отрезке [-π, π].

8. y=1/3cos(2x) на отрезке [-2π, 2π].

9. y=3cos(x) на отрезке [-2π, 2π].

10. y=4cos(x) на отрезке [-2π, 2π].

11. y=1-cos(x) на отрезке [-π, π].

12. y=2+cos(2x) на отрезке [0, 3π].

13. y=2-sin(x) на отрезке [-2π, 2π].

14. y=2+sin(x) на отрезке [-π, π].

15. y=3-sin(x) на отрезке [0, 3π].

Кусочно-линейный метод построения графика

Составим программу построения графика функции

, используя кусочно-линейный метод.

Алгоритм действия следующий:

1. Из условия задачи следует, что X_min = a, Х_тax= b.

2. Предельные значения функции для данной области значений аргумента х определим, используя подпрограмму поиска максимума. Тогда 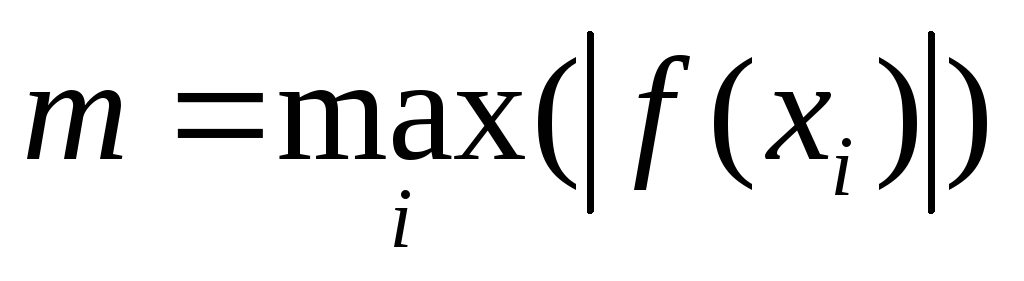в массиве чисел

y_i = │f(x_i)│, где х_i = a + i∙h, ,;

3. Зададим границы графического окна. В программе будем строить график данной функции 2 раза – в пределах следующих графических окон:

а) X_gmin=100; X_gmax=500; Y_gmin= 50; Y_gmax=300

---

б) X_gmin=550; X_gmax=620; Y_gmin= 10; Y_gmax=100.

4. Проведем преобразования формул (*) и получим:

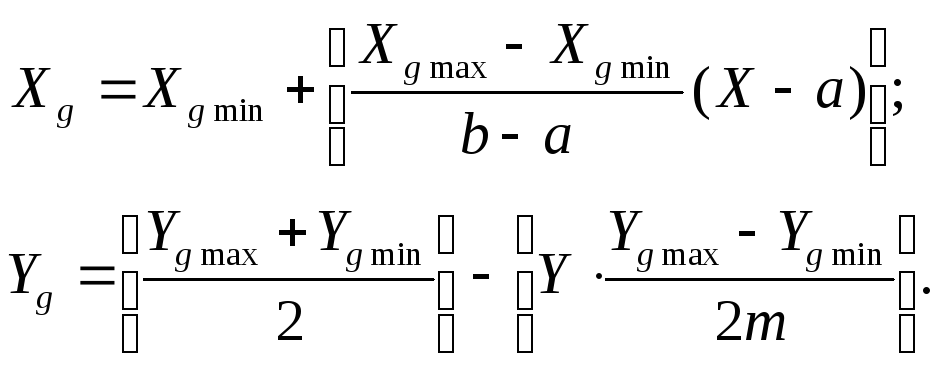
Тогда построение графика функции на экране происходит установкой точек (X_g,, Y_g) соответствующих координатам математическим (x_i, f(x_i)) и эти точки соединяются отрезками ломаной с применением процедуры lineto.

Оси координат на графическом экране строятся с учетом формул для экранного начала координат:

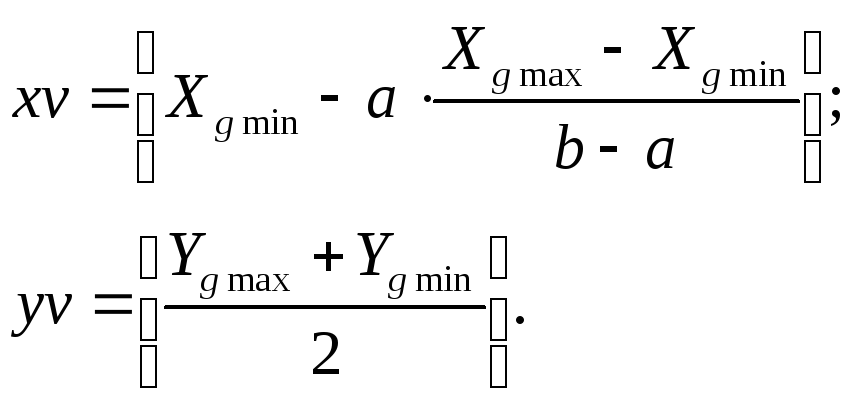
Программа построения графиков:

Program grafik;

Uses crt, graph;

Var d, m, n, i,j: integer;

a, b: real;

Function f (x: real): real;

Begin if x<>0 then f:=x*x*sin(1/x);

End;

Procedure grafun(xgmin,xgmax,ygmin,ygmax,n:integer;a,b:real);

Var h, m, x, t1, t2:real;

i, xg, yg, xv, yv: integer;

Begin h:= (b-a)/n;

m:=abs(f(а));

for i:=1 to n do

if m<abs(f(a+i*h)) then m:=abs(f(a+i*h));

{отношение экранных координат к математическим}

t1:=(xgmax-xgmin)/(b-a);

t2:=(ygmax-ygmin)/(2*m);

{задается цвет и стиль закраски}

Setfillstyle(1, 15);

Bar(xgmin-5, ygmin-5, xgmax+5, ygmax+5);

{задается экранное начало координат}

xv:=round(xgmin-a*t1);

yv:=round((ygmin+ygmax)/2);

setcolor(1);

{нарисовать оси}

Line(xv, ygmin, xv, ygmax);

Line(xgmin, yv, xgmax, yv);

{устанавливаем курсор в начало графика}

Moveto(xgmin, yv-round(f(a)*t2));

Setcolor(4);

for i:=1 to n do

begin x:=a+i*h;

{формулы связи графических и математических координат}

xg:=xgmin+round((x-a)*t1);

yg:=yv-round(f(x)*t2);

lineto(xg, yg);

end;

End;

Begin clrscr; {Очистка экрана}

Writeln(‘ввод a, b, n’);

Readln(a,b,n);

i:=detect;

Initgraph(i, j, ‘ ’);

SetBkColor(7);{задан светло-серый цвет фона}

grafun(100, 500, 50, 300, n, a, b);{первый график строится пределах графического окна (100, 500, 50, 300)}

grafun(550, 620, 10, 100, 200, -0.1, 0.1) {второй график строится в пределах графического окна (550, 620, 10, 100)};

repeat until keypressed; {функция keypressed предназначена для работы с клавиатурой. Она принимает значение true, если буфер клавиатуры не пуст и false, если буфер клавиатуры пуст, эту функцию удобно использовать пока не нажата клавиша}

---

closegraph;

End.

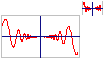
Рисунок 2

Данная программа строит 2 графика. Первый график строится пределах графического окна (100, 500, 50, 300), а второй график строится в пределах графического окна (550, 620, 10, 100). На примере второго графика показано, какие параметры n, a, b могут быть выбраны для подробного построения искомого графика. В первом случае параметры n, a, b устанавливаются пользователем произвольно.

---

Лабораторная работа №2

Построить график заданной функции y=f(x). График построить в пределах данного графического окна (X_gmin, X_gmax, Y_gmin, Y_gmax). Выбрать произвольно цвет фона, цвет изображения.

№ варианта	Функция	Пределы графического окна
1		(130, 530, 30; 430)
2		(100, 500, 150, 400)
3		(150, 550, 50, 400)
4		(130, 530, 40, 310)
5		(80, 480, 100, 400)
6		(50, 450, 100, 400)
7		(100, 500, 150, 400)
8		(150, 550, 150, 400)
9		(50, 450, 100, 400)
10		(50, 450, 80, 330)
11		(30, 430, 30, 430)
12		(50, 550, 30, 530)
13		(40, 500, 50, 350)
14		(40, 500, 50, 350)
15		(50, 550, 30, 530)

---

Пример компьютерной научной графики

Условные цвета, условное контрастирование. Интересный прием современной научной графики – условная раскраска. Она находит широчайшее применение в самых разных приложениях науки.

Приведем примеры. В различных исследованиях температурных полей встает проблема наглядного представления результатов. Самый простой - привести карту (чертеж, план), в некоторых точках которой обозначены значения температуры.

Другой способ – набор изотерм. Но можно добиться еще большей наглядности, учитывая, что большинству людей свойственно, сравнивая разные цвета, воспринимать красный как «горячий», голубой как «холодный», а все остальные - между ними. Допустим, что на некоторой территории температура в данный момент имеет в разных местах значения от -25°С до + 15°С. Разделим этот диапазон на участки с шагом, равным, например, 5°

[-25,-20], [-20,-15],...,[+10,+15],

и закрасим первый из них в ярко-голубой, последний - в ярко-красный, а все остальные - в промежуточные оттенки голубого и красного цветов. Получится замечательная наглядная картина температурного поля.

Пример. Условная раскраска неравномерно нагретого стержня в разные моменты времени (по заранее заготовленным данным).

Рассмотрим динамику изменения температуры в стержне длиной 4 м с теплоизолированными концами, температура на которых поддерживается постоянной и равна 3°С с заданным начальным условием.

Ограничимся пятью узлами на пространственной сетке. В начальный момент (t = 0) температура в пяти узлах задана:

u = 3,0000, u = 3,667, и= 4,333, и= 5,000, и= 3,0000.

Из краевых условий получаем и= и= 3,000, где .

Решая данную задачу, получаем распределение температуры по длине стержня в узлах пространственной сетки в разные моменты времени. (см. решение задачи в части II: «Компьютерное моделирование физических процессов»)

---