Файл: Лекция_3.4.Элементы теории корреляции.doc

Здесь - наблюдаемые значения,;;- частота появления пары;- частота появления;- частота появления;n – число всех наблюдений. Отсюда с учётом частот появлений переменных и

; ;

; ;.

Подставив эти суммы в формулы (2), получим:

;

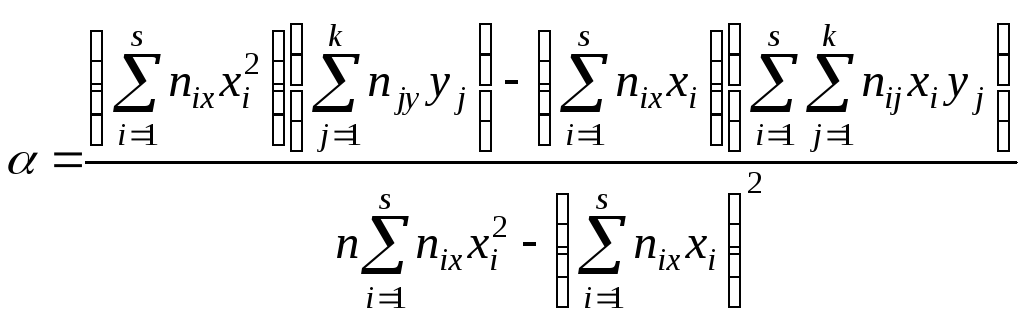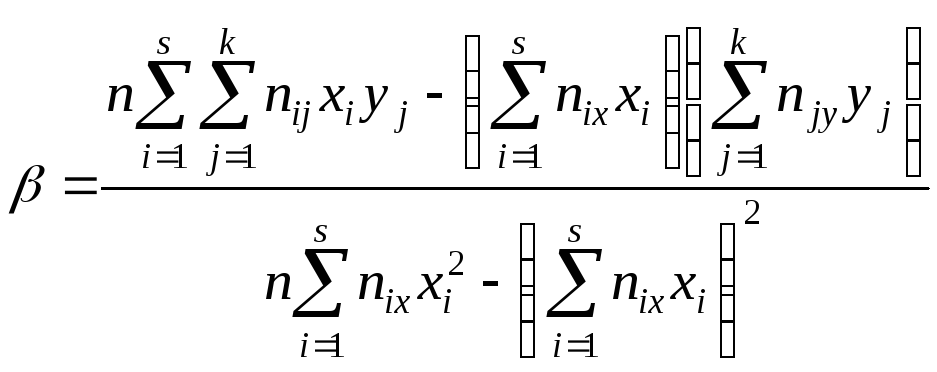. (4)

---

П.2. Линейная корреляция.

Пусть имеется выборка объёмаn. Напомним, что ковариация cov(X,Y) определяется равенством

,

где ,- выборочные средние;- выборочное среднее произведения.

Выборочные дисперсии определяются соотношениями:

;

.

Коэффициент корреляции: .

Тогда, уравнение прямой регрессии Y на X имеет вид

. (5)

Аналогично, уравнение прямой регрессии X на Y имеет вид

. (6)

Величины называютсякоэффициентами линейной регрессии и обозначаются:

; . (7)

П.3. Криволинейная (нелинейная) корреляция.

Если линии регрессий отличны от прямых, то коэффициент корреляции не даёт полного представления о силе связи между величинами X и Y. В этом случае за меру зависимости берут корреляционные отношения, которые вычисляют по формулам:

, , (8)

где

; ;

---

; ;

; .

Корреляционное отношение обладает следующими свойствами:

1) оно всегда заключено между 0 и 1, т.е. и;

2) необходимое и достаточное условие отсутствия корреляционной зависимости признака Y от признака X состоит в том, что ;

3) если корреляционные отношения , то между признакомY и признаком X существует функциональная зависимость ;

4) выборочный коэффициент корреляции между признаками X и Y всегда по абсолютной величине не больше корреляционных отношений и:,;

5) если , а, тои.

Для выбора и обоснования типа кривой регрессии нет универсального метода. Односторонняя зависимость между величинами X и Y может быть описана, например, с помощью полиномиальной регрессии:

Рассмотрим случай, когда график рассеяния значений случайных величин X и Y приближён к параболе

(9)

Пусть дано распределение двумерной выборки для величин X и Y . На основании этих данных составим следующую таблицу

---

			…
			…
			…

где каждому x_i будет соответствовать среднее значение с частотой. Тогда, используя метод наименьших квадратов для нахождения α, β,с, получим систему нормальных уравнений

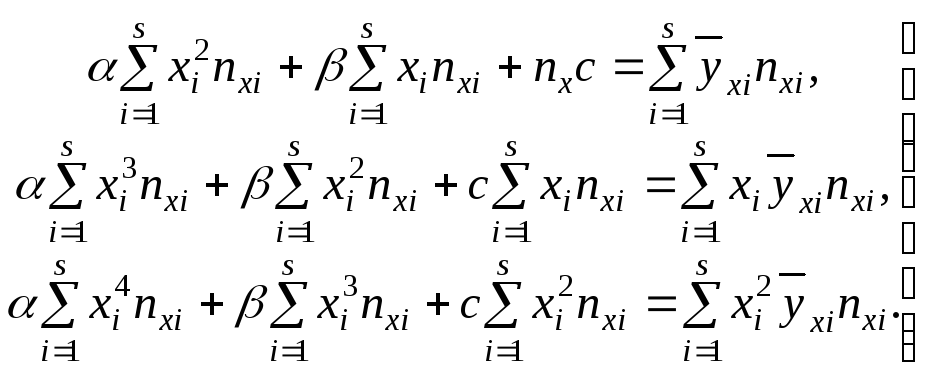(10)

Решая систему (10), находим коэффициенты α, β, с, из которых с является выравнивающей постоянной, α и β – параметры регрессии, характеризующие зависимость величины Y от X.

Если вместо уравнения (9) взять

, (11)

то для вычисления α и с получим нормальную систему уравнений

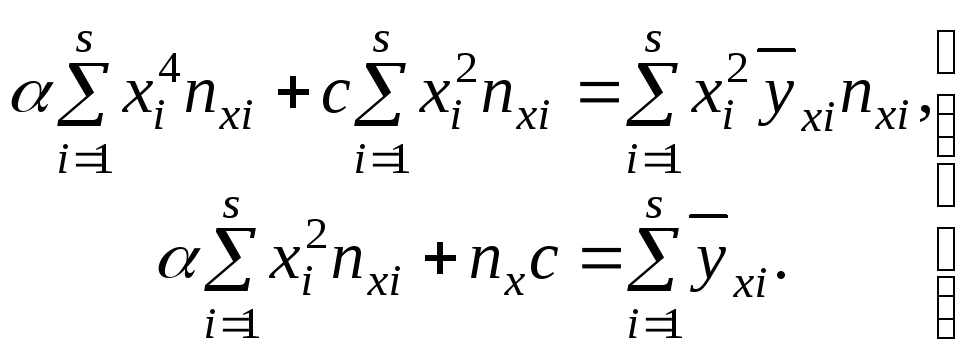(12)

При выборе формы корреляционной зависимости Y от X в виде уравнения гиперболы

---

(13)

получаем систему уравнений

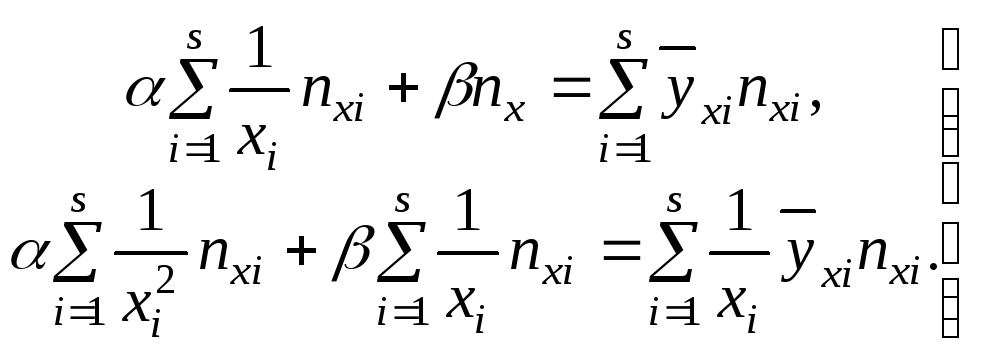(13)

В случае гиперболической регрессии X на Y уравнение гиперболы имеет вид

. (14)

Тогда для определения c и d получаем систему

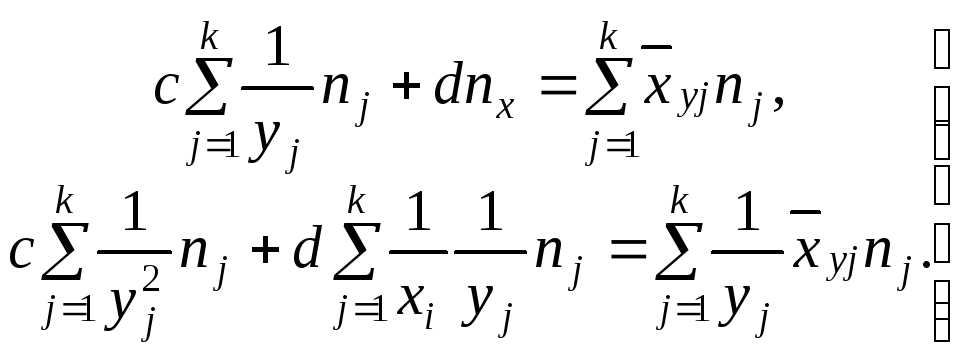(14)

Выбор уравнений (2), (11), (13), (14) производится по корреляционному полю. Могут быть и другие виды уравнений регрессии Y на X и X на Y.

П.4. Ранговая корреляция.

Пусть выборка объёма n содержит независимые объекты, которые обладают двумя качественными признаками: А и В. Под качественным подразумевают признак, который невозможно измерить точно, но он позволяет сравнивать объекты между собой и, следовательно, расположить их в порядке убывания или возрастания качеств. Для определённости условимся располагать объекты в порядке ухудшения качества.

Расположим сначала объекты в порядке ухудшения качества по признаку А. Припишем объекту, стоящему на i-ом месте, число – ранг x_i, равный порядковому номеру объекта: x_i=i. Затем расположим объекты в порядке убывания качества по признаку В и припишем каждому из них ранг (порядковый номер) y_i, причём (для удобства сравнения рангов) индекс i при y по-прежнему равен порядковому номеру объекта по признаку А.

В результате получим две последовательности рангов:

по признаку А x₁ x₂ … x_n

по признаку В y₁ y₂ … y_n

Для оценки степени связи признаков А и В служат, в частности, коэффициенты ранговой корреляции Спирмена и Кенделла.

Выборочный коэффициент ранговой корреляции Спирмена находят по формуле:

,

где ,n – объем выборки.

Абсолютная величина коэффициента ранговой корреляции Спирмена не превышает единицы: .

---