Добавлен: 19.10.2018
Просмотров: 1244
Скачиваний: 10
СОДЕРЖАНИЕ
Задание 1. Решение задач линейного программирования в MS Excel.
Варианты заданий. Решить задачи ЛП в MS Excel.
Задание 2. Решение транспортной задачи в пакете MS Excel.
Варианты заданий. Решить транспортную задачу в MS Excel.
Задание 3. Решение задачи о рюкзаке приближенными и точными алгоритмами.
Задание 4. Реализация алгоритмов решения задачи коммивояжёра.
Методические указания к выполнению
контрольной работы дисциплины
«информационные технологии»
ГР. АХ-14-ЗП
Задание 1. Решение задач линейного программирования в MS Excel.
Задачи линейного программирования (ЛП) являются математическими моделями многих практических задач, возникающих в экономике, планировании, управлении и других областях. Кроме того, в ряде случаев решение задачи линейного программирования является этапом решения более сложной задачи оптимизации (например, задачи целочисленного линейного программирования) [1,3,6,7].
Под задачей
линейного программирования понимается
задача поиска решения
![]() ,
которое удовлетворяет системе линейных
равенств или неравенств и на котором
достигается максимальное или минимальное
значение линейной целевой функции
f(x).
,
которое удовлетворяет системе линейных
равенств или неравенств и на котором
достигается максимальное или минимальное
значение линейной целевой функции
f(x).
Общая постановка задачи ЛП:
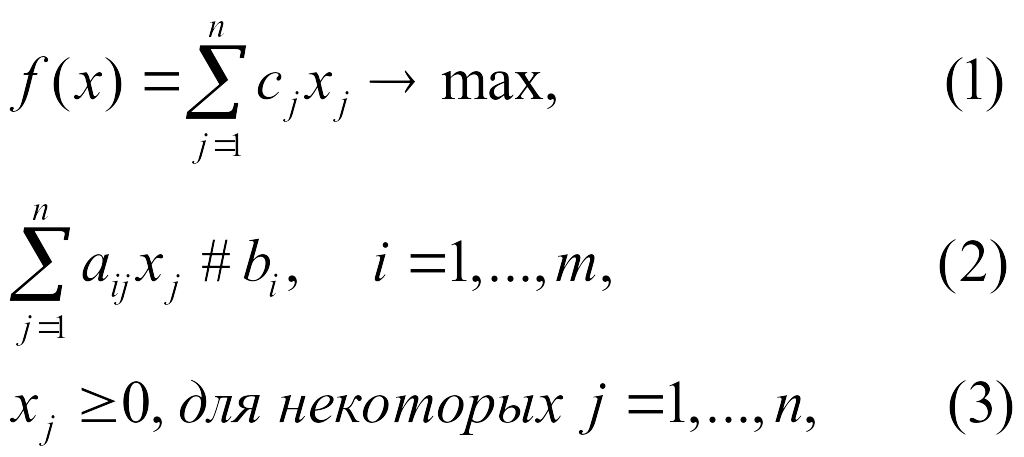
где под знаком “#” понимается любой из знаков “≤”, “≥” и “=”, причем в одной задаче ЛП могут встречаться знаки всех трех типов.
Классическим примером содержательной задачи, математической моделью
которой является задача линейного программирования, служит задача оптимального планирования производства.
Для решения задач ЛП малой и средней размерности (десятки и сотни переменных) используются стандартные программные продукты. Для решения задач ЛП большой размерности (тысячи переменных) требуется разработка специального программного обеспечения.
Далее рассмотрим решение задач ЛП в пакетах MathCAD [5] и MS Excel [4] на примере задачи с двумя переменными, которые, без ограничения общности, будем обозначать x и y.
Решение задачи линейного программирования в Microsoft Excel. Рассмотрим решение задачи ЛП
Требуется найти максимум целевой функции
f (x) = 4x + 2y max,
2x + 3y ≤ 18,
-x + 3y ≤ 9,
2x - y ≤ 10,
x 0, y 0.
Сначала выделим ячейки под значения под значения переменных x и y, например, ячейки С3 и С4. Далее в ячейку С6 введем целевую функцию
= 4*С3 + 2*С4.
В ячейки В9 : В11 введем левые части ограничений
= 2*C3 + 3*C4,
= - 1*C3 + 3*C4,
= 2*C3 - 1*C4,
а в ячейки С9 : С11 – правые части ограничений (см. рис.2).
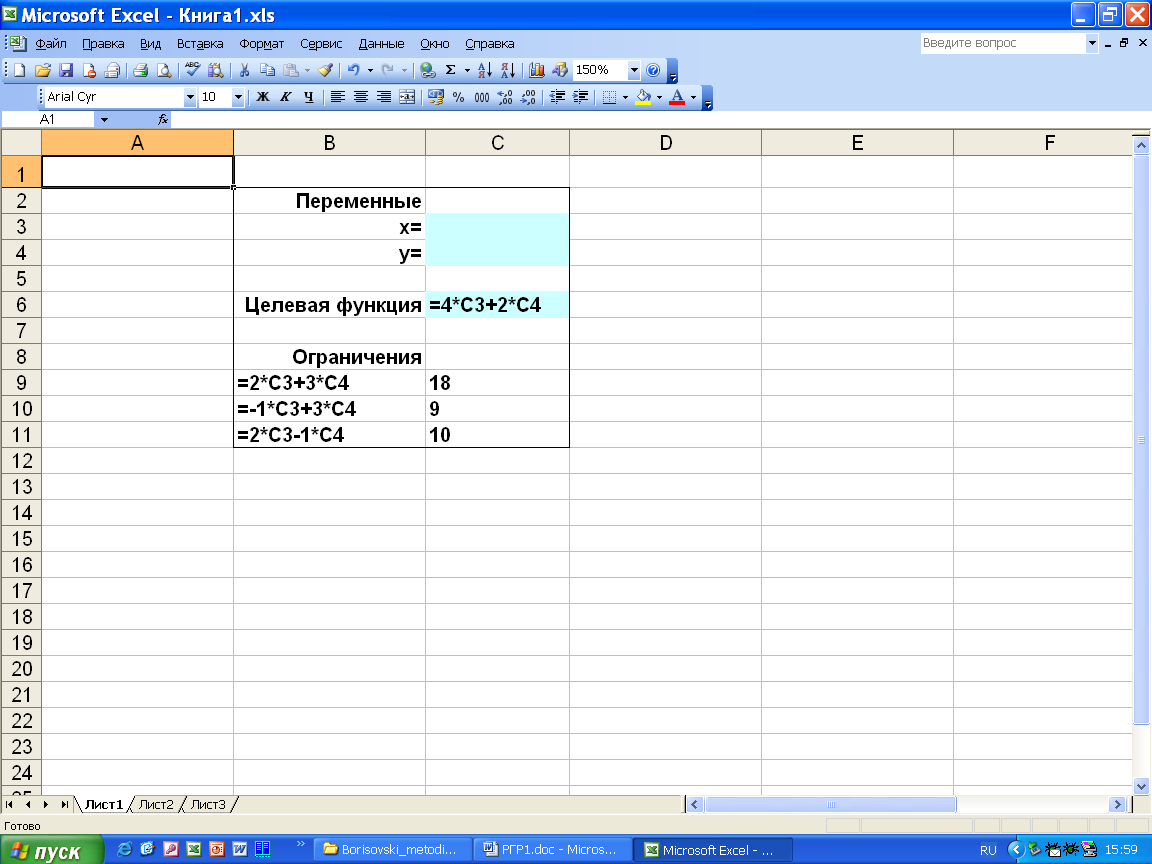
Рис. 2. Диапазоны, отведенные под переменные, целевую функцию и ограничения.
После этого выберем в главном меню команду Сервис, Поиск решения. Если в меню Сервис этого пункта нет, нужно установить надстройку. Для этого выберем в меню Сервис пункт Надстройки. В диалоговом окне "Надстройки" нужно найти в списке надстроек "Поиск решения" и установить слева от него флажок. Загрузится Решатель. В дальнейшем при запуске Ехсеl Решатель будет загружаться автоматически, пока не будет снят флажок в окне "Надстройки".
Заполним открывшееся диалоговое окно Поиск решения, как показано на рис. 3.
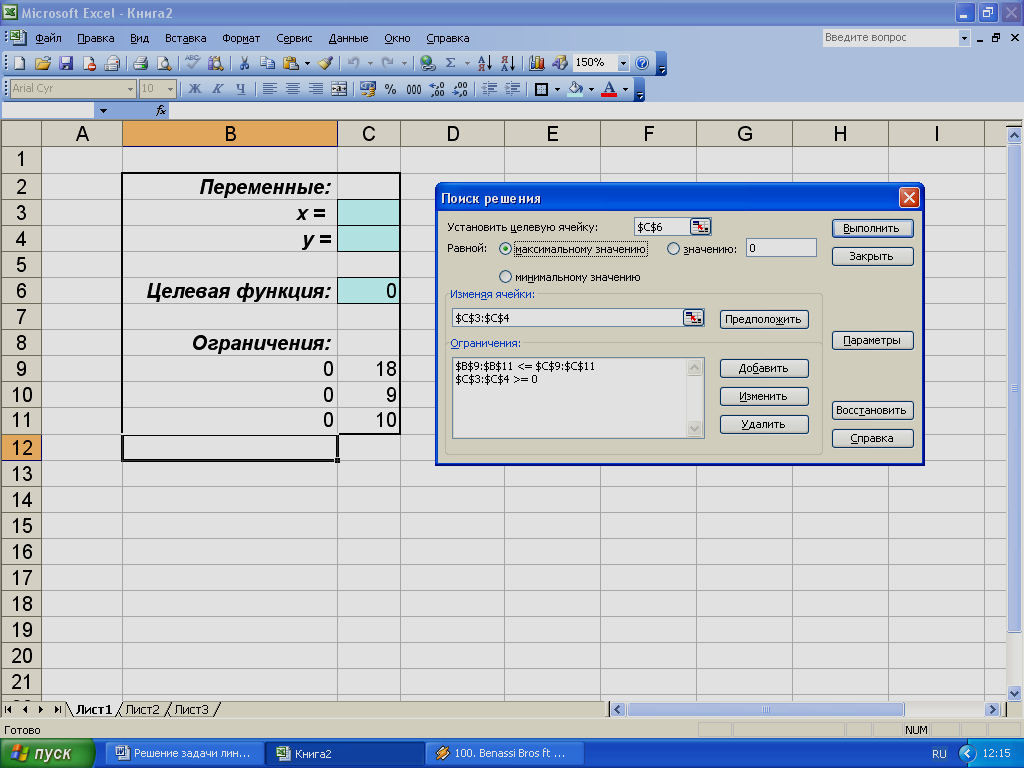
Рис. 3. Диалоговое окно Поиск решений.
После нажатия на кнопку Выполнить открывается окно Результаты поиска решения, которое сообщает, что решение найдено (рис. 4).
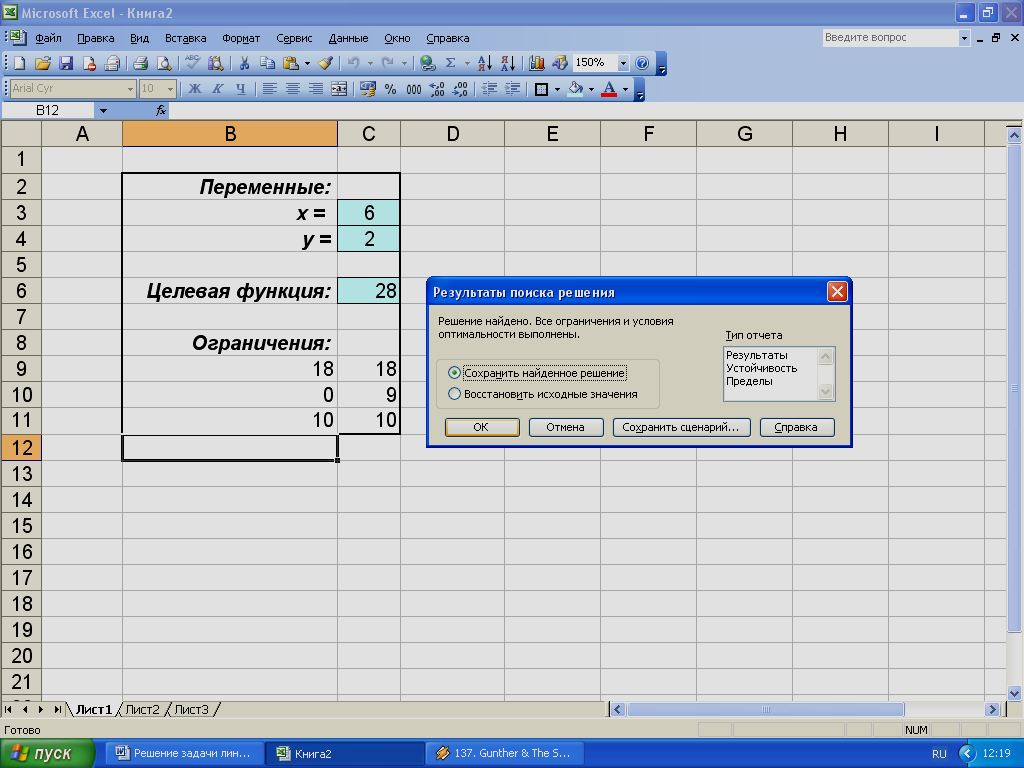
Рис.4. Диалоговое окно Результаты поиска решения.
Оптимальное решение находится в ячейках C3 и C4, а оптимальное значение целевой функции – в ячейке C6 (рис. 5).
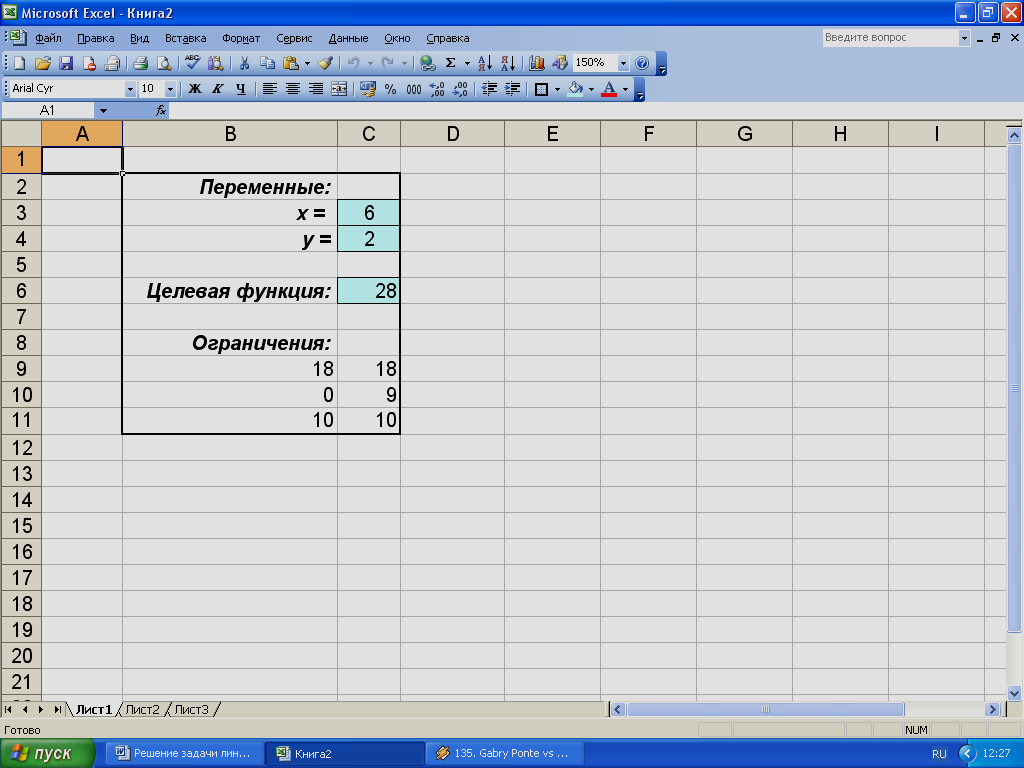
Рис.5. Результаты решения.
Задачи ЛП в общем случае решаются аналогично в обоих пакетах.
Варианты заданий. Решить задачи ЛП в MS Excel.
|
1) 3x1 + 4x2 → max
6x1 + 11x2 ≤ 50 12x1 + 6x2 ≤ 54 6x1 − 3x2 ≥ 15 28x1 + 56x2 ≥ 112 x1, x2 ≥ 0.
|
2) 8x1 + 2x2 → max
22x1 + 7x2 ≤ 77 4x1 + 9x2 ≥ 18 15x1 + 10x2 ≤ 60 4x1 + 8x2 ≤ 16 x1, x2 ≥ 0.
|
|
3) 15x1 +13x2 → max
12x1 + 6x2 ≤ 32 8x1 ≤ 9 6x1 +14x2 ≤ 39 4x1 +15x2 ≤ 18 x1, x2 ≥ 0.
|
4) 12x1 + 4x2 → max
11x1 + 5x2 ≤ 31 7x1 ≤ 7 2x1 −16x2 ≥ 6 9x1 + 3x2 ≤ 38 x1, x2 ≥ 0.
|
|
5) 7x1 + 6x2 → max
16x1 − 2x2 ≤ 18 8x1 + 4x2 ≤ 20 13x1 + 3x2 ≤ 4 x1, x2 ≥ 0.
|
6) 7x1 + 5x2 → max
4x1 + 4x2 ≤ 26 3x1 − 16x2 ≥ −18 14x1 − 2x2 ≤ 10 18x1 + 16x2 ≤ 8 x1, x2 ≥ 0. |
−3x1 + 16x2 ≤ 32 5x1 + 6x2 ≤ 17 14x1 + 5x2 ≤ 30 4x1 + 4x2 ≤ 5 x1, x2 ≥ 0. |
8) −2x1 → max
5x1 + 5x2 ≤ 39 −2x1 + 14x2 ≤ 5 2x1 − 12x2 ≥ 6 −x1 + 10x2 ≤ 6 x1, x2 ≥ 0. |
5x1 + 15x2 ≤ 16 2x1 + 3x2 ≥ −1 − x1 + 14x2 ≤ 7 − x1 + 4x2 ≥ 1 x1, x2 ≥ 0.
|
11x1 +2x2 ≤ 42 −2x1 + 8x2 ≤ 19 14x1 + 6x2 ≤ 38 13x1 + 2x2 ≤ 26 x1, x2 ≥ 0. |
|
11) 3x1 + 5x2 → max
15x1 + 10x2 ≤ 60 2x1 − 3x2 ≥ 1 28x1 + 56x2 ≥ 112 10x1 + 15x2 ≤ 45 x1, x2 ≥ 0. |
12) 2x1 + 11x2 → max
16x1 + x2 ≤ 19 13x1 + 20x2 ≤ 14 10x1 + 6x2 ≤ 13 6x1 − 3x2 ≤ 6 x1, x2 ≥ 0.
|
|
13) 13x1 + 8x2 → max
9x1 + 3x2 ≤ 28 9x1 + 8x2 ≤ 35 x1 + 8x2 ≤ 40 2x1 + 7x2 ≤ 20 x1, x2 ≥ 0.
|
14) 5x1 + 9x2 → max
8x1 − 5x2 ≤ −3 −3x1 + 12x2 ≤ 42 2x1 + x2 ≤ 44 5x2 ≤ 11 x1, x2 ≥ 0.
|
|
15) x1 + 6x2 → max
14x1 + 21x2 ≤ 28 20x1 + 35x2 ≤ 70 12x1 − 9x2 ≥ 12 21x1 + 15x2 ≤ 75 x1, x2 ≥ 0.
|
16) 2x1 + 3x2 → max
8x1 + 9x2 ≤ 36 10x1 +14x2 ≥ 12 4x1 + 8x2 ≤ 16 6x1 − 3x2 ≤ 9 x1, x2 ≥ 0.
|
|
17) 2x1 + x2 → max
14x1 + 10x2 ≤ 23 2x1 + 8x2 ≤ 25 15x1 + 6x2 ≤ 32 18x1 − 5x2 ≤ 26 x1, x2 ≥ 0.
|
18) 5x1 + 6x2 → max
13x1 + 5x2 ≤ 18 3x1 + x2 ≤ 4 4x1 + 8x2 ≤ 10 2x1 +11x2 ≥ 6 x1, x2 ≥ 0.
|
|
19) 4x1 + x2 → max
x1 + 5x2 ≤ 6 16x1 + 4x2 ≤ 12 10x1 + x2 ≤ 6 3x1 − 3x2 ≤ 43 x1, x2 ≥ 0. |
20) 4x1 + 5x2 → max
9x1 ≤ 15 15x2 ≤ 6 −2x1 + 13x2 ≤ 31 2x1 + 3x2 ≤ 39 x1, x2 ≥ 0. |
|
21) 7x1 + 2x2 → min
3x1 + 12x2 ≤ 30 10x1 + 3x2 ≤ 24 9x1 − 2x2 ≥ 12 11x1 + 24x2 ≥ 48 x1, x2 ≥ 0.
|
22) 3x1 + 2x2 → min
2x1 + 7x2 ≤ 17 4x1 + x2 ≥ 8 5x1 + 10x2 ≤ 20 3x1 + 5x2 ≤ 15 x1, x2 ≥ 0.
|
|
23) 5x1 + 7x2 → max
2x1 + 8x2 ≤ 24 6x1 ≤ 9 3x1 +10x2 ≤ 30 4x1 +12x2 ≤ 35 x1, x2 ≥ 0.
|
24) 9x1 + 4x2 → max
13x1 + 2x2 ≤ 22 4x1 ≤ 7 4x1 −10x2 ≥ 5 7x1 + 13x2 ≤ 38 x1, x2 ≥ 0. |
|
25) 2x1 + 6x2 → max
11x1 − 4x2 ≤ 22 6x1 + 4x2 ≤ 21 3x1 + x2 ≤ 14 x1, x2 ≥ 0.
|
26) 3x1 + 2x2 → max
5x1 + 4x2 ≤ 16 3x1 − 10x2 ≥ −11 4x1 − 5x2 ≤ 10 3x1 + 10x2 ≤ 8 x1, x2 ≥ 0.
|
|
27) x1 + 7x2 → max
−2x1 + 13x2 ≤ 26 4x1 + 9x2 ≤ 28 12x1 + 5x2 ≤ 32 x1 + 2x2 ≤ 5 x1, x2 ≥ 0. |
28) 3x1 → max
7x1 + 5x2 ≤ 29 −4x1 + 12x2 ≤ 5 2x1 − 9 x2 ≥ 6 −x1 + 13x2 ≤ 7 x1, x2 ≥ 0.
|
|
29) 4x1 + 7x2 → max
5x1 + 15x2 ≤ 16 2x1 + 3x2 ≥ −1 − x1 + 14x2 ≤ 7 − x1 + 4x2 ≥ 1 x1, x2 ≥ 0.
|
30) 3x1 + 2x2 → max
12x1 +7x2 ≤ 32 −4x1 + 8x2 ≤ 15 12x1 + 6x2 ≤ 38 10x1 + 2x2 ≤ 26 x1, x2 ≥ 0.
|
Задание 2. Решение транспортной задачи в пакете MS Excel.
Транспортная задача – это задача о минимизации транспортных расходов, связанных с обеспечением пунктов потребления определенным количеством однородной продукции, производимой в нескольких пунктах производства [1, 3, 7]. В общем виде задача может быть сформулирована следующим образом.
Однородный
продукт, сосредоточенный в
![]() пунктах производства, необходимо
распределить между
пунктах производства, необходимо
распределить между
![]() пунктами потребления. Стоимость перевозки
единицы продукции известна для всех
маршрутов. Необходимо составить такой
план перевозок, при котором запросы
всех пунктов потребления были бы
удовлетворены за счет имеющихся продуктов
в пунктах производства и общие транспортные
расходы по доставке продуктов были бы
минимальными.
пунктами потребления. Стоимость перевозки
единицы продукции известна для всех
маршрутов. Необходимо составить такой
план перевозок, при котором запросы
всех пунктов потребления были бы
удовлетворены за счет имеющихся продуктов
в пунктах производства и общие транспортные
расходы по доставке продуктов были бы
минимальными.
Примем
следующие обозначения: i
– номер пункта производства, j
–номер пункта потребления,
![]() –
количество продукта, имеющееся в i-ом
пункте производства,
–
количество продукта, имеющееся в i-ом
пункте производства,
![]() – количество продукта, необходимое для
j-го
пункта потребления,
– количество продукта, необходимое для
j-го
пункта потребления,
![]() – стоимость перевозки единицы продукта
из i-го
пункта производства в j-й
пункт потребления,
– стоимость перевозки единицы продукта
из i-го
пункта производства в j-й
пункт потребления,
![]() – количество груза, планируемого к
перевозке из i-го
пункта производства в j-й
пункт потребления, i=1,2,…,m;
j=1,2,…,n.
Математическая модель транспортной
задачи будет выглядеть следующим
образом:
– количество груза, планируемого к
перевозке из i-го
пункта производства в j-й
пункт потребления, i=1,2,…,m;
j=1,2,…,n.
Математическая модель транспортной
задачи будет выглядеть следующим
образом:
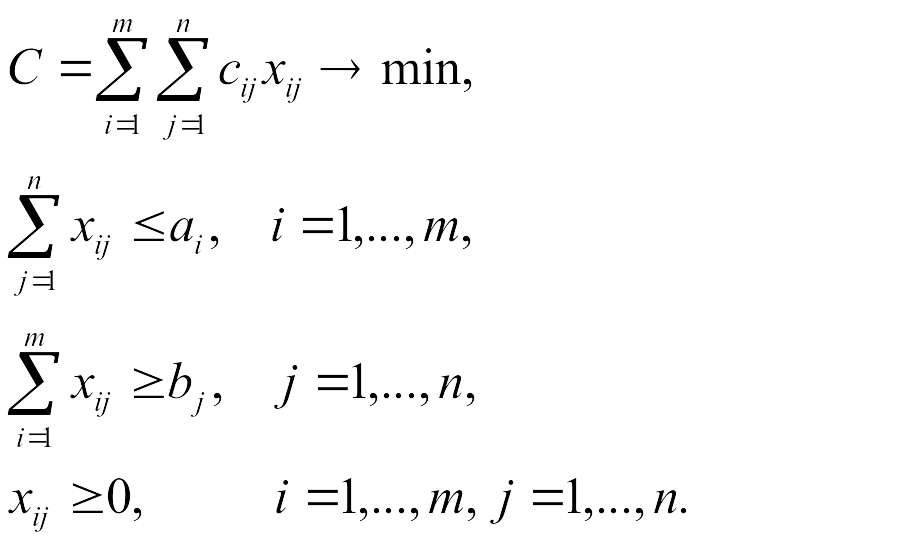
Условия задачи удобно записывать в виде таблицы, которая называется матрицей планирования:
-
с11 с12 … с1n
. . .
сm1 сm2 … сmn
a1
…
am
b1 b2 … bn
Рассмотрим решение транспортной задачи в табличном процессоре MS Excel. Так как транспортная задача является частным случаем задачи линейного программирования, то эту задачу можно решать так, как описано выше. Однако благодаря свойствам задачи, ее можно записать в более компактной форме.
Рассмотрим транспортную задачу, матрица планирования которой имеет вид:
-
Bj
Ai
B1
B2
B3
B4
B5
A1
14
25
18
19
23
33
A2
2
17
16
24
2
25
A3
29
3
7
15
22
25
A4
5
20
17
23
10
17
33
11
11
11
34
bj ai
Для решения транспортной задачи введем данные, как показано на рис.6.
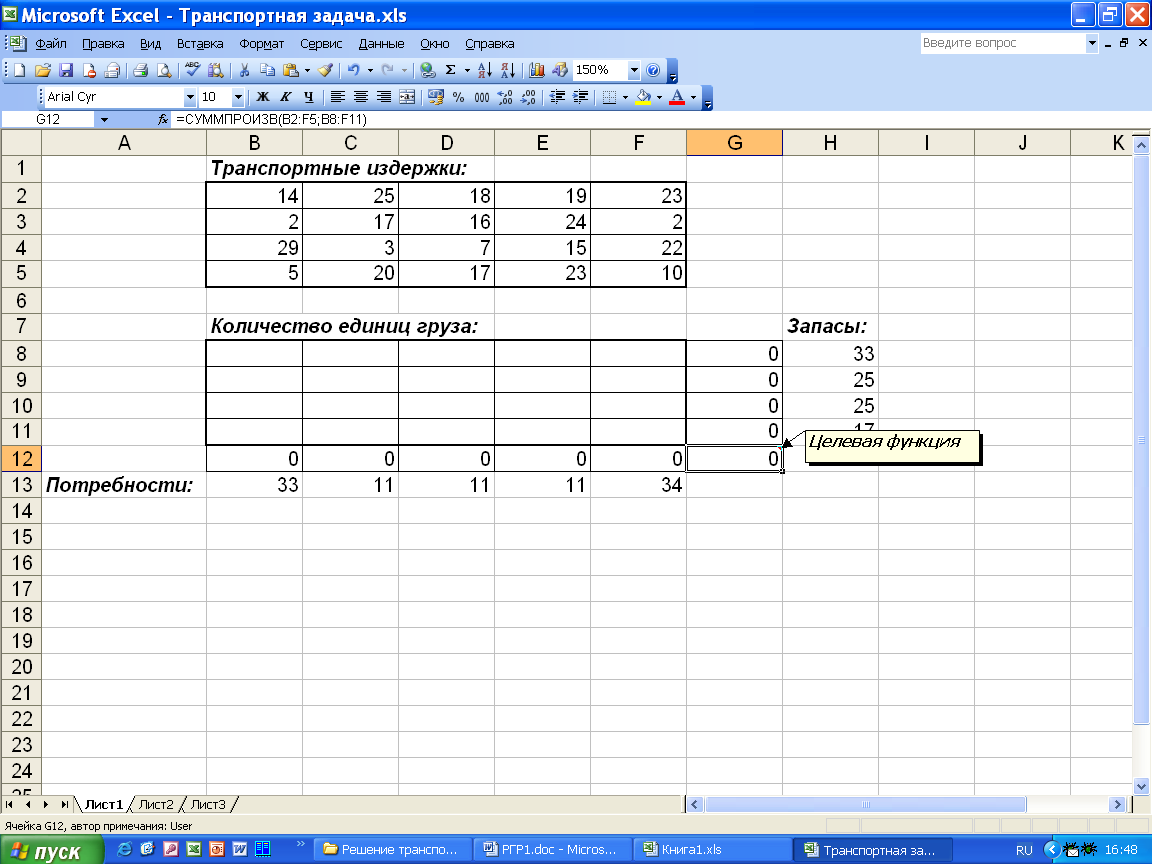
Рис.6. Исходные данные транспортной задачи.
В ячейки B2 : F5 введем стоимость перевозок. Ячейки B8 : F11 отведены под значения объемов перевозок, пока неизвестные. В ячейки H8 : H11 введены объемы производства, а в ячейки B13 : F13 - потребности (спрос) в продукции в пунктах потребления.
В ячейку G12 вводится целевая функция
= СУММПРОИЗВ (B2 : F5; B8 : F11) .
В ячейки B12 : F12 вводятся формулы
= СУММ (B8 : B11),
= СУММ (C8 : C11),
= СУММ (D8 : D11),
= СУММ (E8 : E11),
= СУММ (F8 : F11),
определяющие объем продукции, ввозимой в пункты потребления. В ячейки
G8 : G11 введены формулы
= СУММ (B8 : F8),
= СУММ (B9 : F9),
= СУММ (B10 : F10),
= СУММ (B11 : F11),
характеризующие объем продукции, вывозимой из пунктов производства.
Далее выбираем команду Сервис, Поиск решения и заполняем открывшееся диалоговое окно Поиск решения, как показано на рис.7.
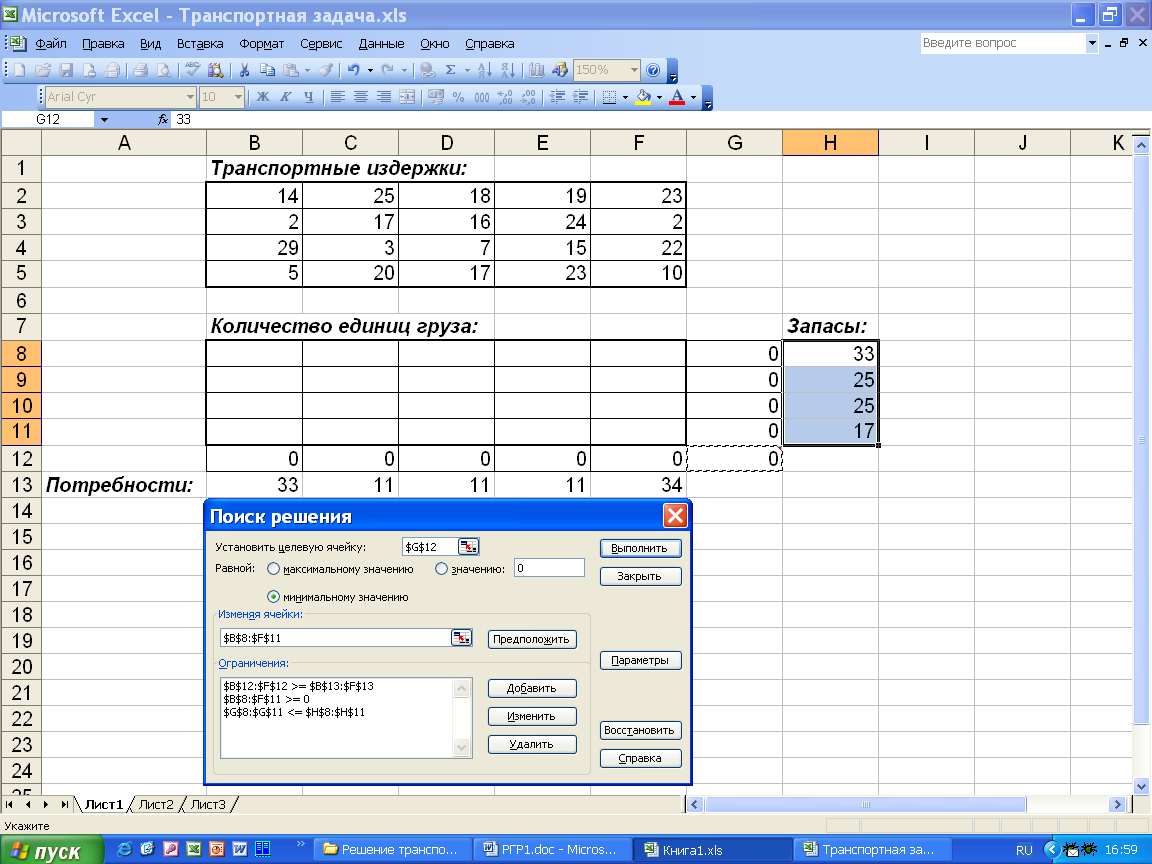
Рис.7. Диалоговое окно Поиск решения для транспортной задачи.
В диалоговом окне Параметры поиска решения установить флажок Линейная модель (рис.8).
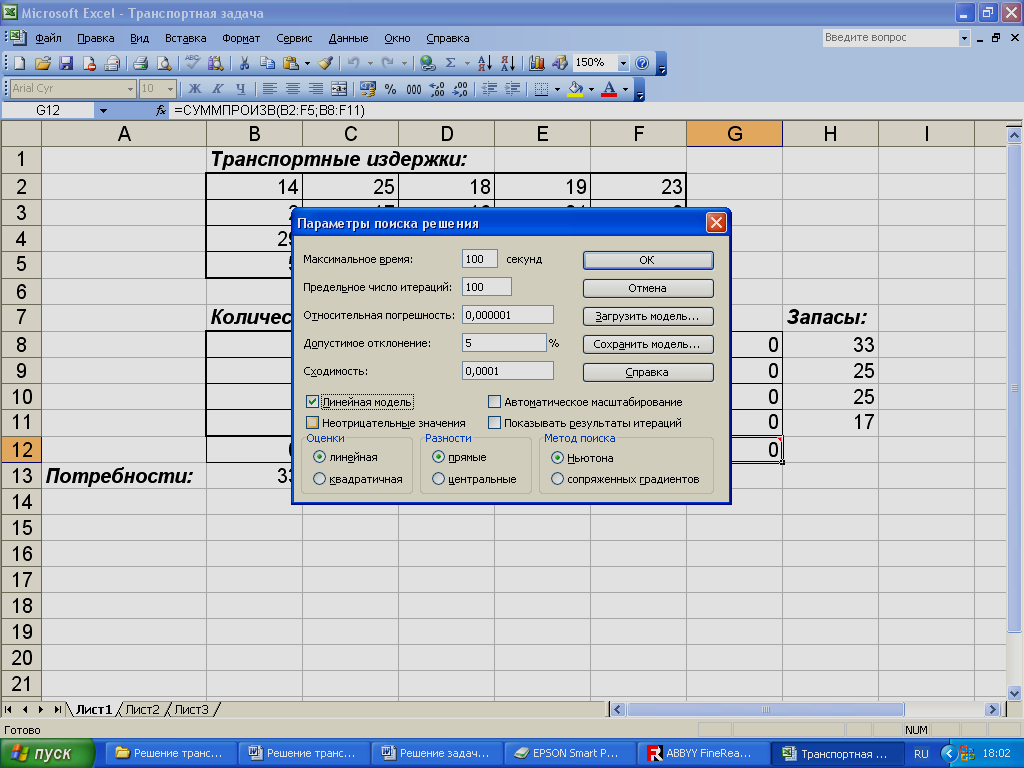
Рис.8. Диалоговое окно Параметры поиска решений.
После нажатия кнопки Выполнить получаем оптимальный план поставок продукции и соответствующие ему транспортные расходы (рис. 9).
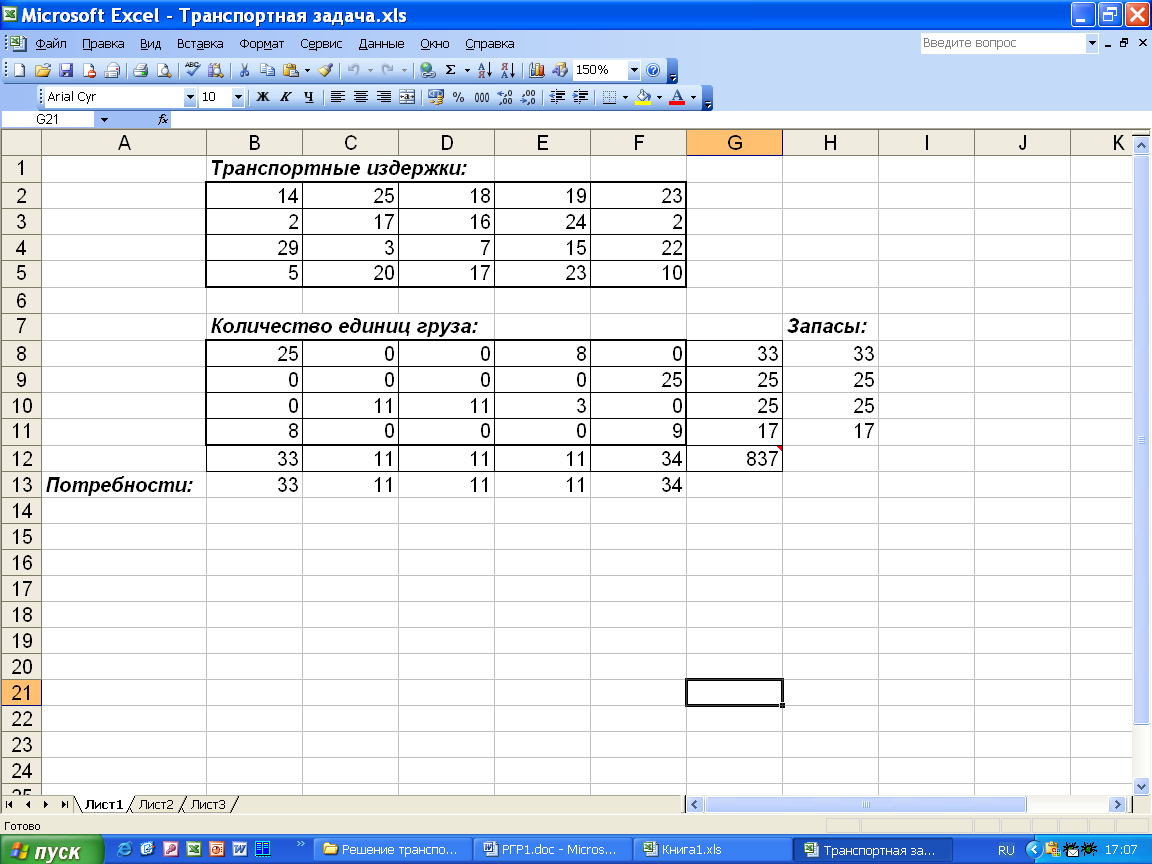
Рис.9. Оптимальное решение транспортной задачи.
Варианты заданий. Решить транспортную задачу в MS Excel.
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Задание 3. Решение задачи о рюкзаке приближенными и точными алгоритмами.
Задача о рюкзаке и ее варианты широко используются для моделирования большого числа практических задач управления, таких как выбор проектов, распределение капитала, комбинаторные аукционы, расположение предметов в системах сборки по заказу и др. [3, 6, 7].
Одним из частных случаев задачи о рюкзаке является одномерная булева задача о рюкзаке, которая может быть сформулирована следующим образом. Рассмотрим рюкзак с объемом равным b. Пусть существует n различных предметов. Предмет j занимает объем aj, при этом его ценность равна cj. Цель задачи состоит в максимизации выгоды от помещенных в рюкзак предметов. Таким образом, задача может быть сформулирована как задача булева линейного программирования в следующем виде:
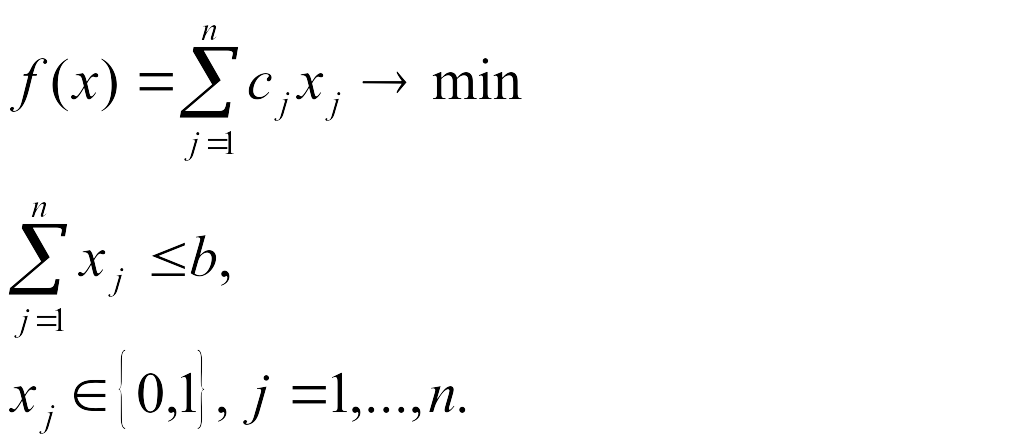
Если условие
![]() заменить условием
заменить условием
![]() ,
то получим задачу об одномерном
целочисленном рюкзаке. В этом случае
имеется n
типов
предметов и требуется определить,
сколько предметов каждого типа нужно
поместить в рюкзак, чтобы они имели
максимальную суммарную ценность.
,
то получим задачу об одномерном
целочисленном рюкзаке. В этом случае
имеется n
типов
предметов и требуется определить,
сколько предметов каждого типа нужно
поместить в рюкзак, чтобы они имели
максимальную суммарную ценность.
Для решения задачи о рюкзаке разработан целый ряд алгоритмов и методов: динамическое программирование [6], метод ветвей и границ [3], метод перебора L-классов [2] и другие.
В случае небольших n одномерная задача о рюкзаке может быть также решена в табличном процессоре MS Excel. При этом исходные данные задачи записываются также, как и для задачи ЛП, но в окне Поиск решения, Ограничения необходимо указать, что переменные являются целыми, либо булевыми (рис. 10).
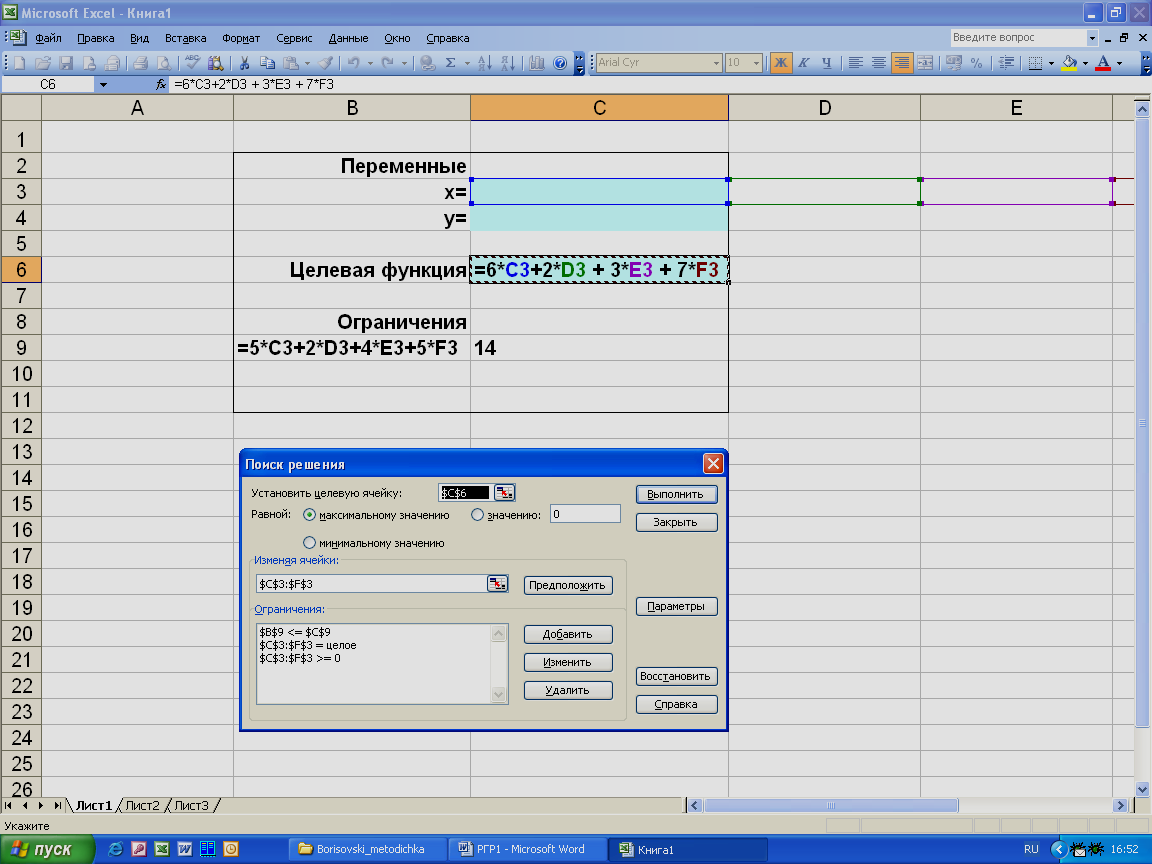
Рис. 10. Диалоговое окно Поиск решения для задачи о рюкзаке.
При больших n точное решение задачи может потребовать значительных затрат машинного времени. Поэтому актуальной является разработка приближенных алгоритмов. Самый известный приближенный алгоритм – это так называемый “жадный” алгоритм. Опишем этот алгоритм по шагам для булевого случая.
«Жадный» алгоритм.
Шаг 1. Упорядочить предметы по не возрастанию удельной полезности cj / aj,
т.е. так, чтобы выполнялось соотношение
![]() ,
,
положить k:=1 и перейти на шаг 2.
Шаг 2. Если ak ≤ b, то положить xk:=1, b:=b – ak, иначе xk:= 0.
Увеличить k на единицу и перейти на шаг 3.
Шаг 3. Если k > n, то алгоритм завершает работу, иначе перейти на шаг 2.
Варианты заданий. Решить задачу о рюкзаке в пакете MS Excel. Разработать алгоритм полного перебора и «жадный» алгоритм для задачи о рюкзаке [8]. Найти точное и приближенное решение задачи о рюкзаке, используя реализованные алгоритмы.
|
1) 6x1+ 2x2+ 3x3+ 7x4 → max
5x1+ 2x2+ 4x3+ 5x4 ≤ 14 xi ≥ 0, xi є Z, i = 1,..,4. |
2) 2x1+ 4x2+ 4x3+ 3x4 → max
2x1+5x2+ 3x3+4x4 ≤ 12 xi ≥ 0, xi є Z, i = 1,..,4.
|
|
3) 3x1+ 6x2+ 5x3+ x4 → max
2x1+ 5x2+4x3+ x4 ≤ 15 xi ≥ 0, xi є Z, i = 1,..,4.
|
4) 2x1+ 2x2+ x3+3x4 → max
2x1+ 3x2+ 2x3+ 3x4 ≤ 13 xi ≥ 0, xi є Z, i = 1,..,4. |
|
5) 5x1+ x2+ x3+ 3x4 → max
4x1+ 3x2+ x3 + 3x4 ≤ 13 xi ≥ 0, xi є Z, i = 1,..,4. |
6) x1+ 5x2+ 2x3+ 3x4 → max
2x1+ 4x2+ 5x3+ 3x4 ≤ 14 xi ≥ 0, xi є Z, i = 1,..,4.
|
|
7) 5x1+ 7x2+ 6x3+ 3x4 → max
4x1+ 5x2+ 8x3+ 3x4 ≤ 14 xi ≥ 0, xi є Z, i = 1,..,4.
|
8) x1+ 7x2+ 3x3+ 4x4 → max
x1+ 5x2+ 2x3+ 3x4 ≤ 13 xi ≥ 0, xi є Z, i = 1,..,4. |
|
9) x1+ 7x2+ 7x3+ 4x4 → max
2x1+ 6x2+ 4x3+ 3x4 ≤ 15 xi ≥ 0, xi є Z, i = 1,..,4.
|
10) 3x1+ 5x2+ 2x3+ 8x4 → max
2x1+ 4x2+ x3+ 6x4 ≤ 15 xi ≥ 0, xi є Z, i = 1,..,4. |
|
11) x1+ 5x2+ 6x3+ 3x4 → max
2x1+ 4x2+ 5x3 + 3x4 ≤ 15 xi ≥ 0, xi є Z, i = 1,..,4.
|
12) 4x1+ 5x2+ 2x3+4x4 → max
2x1+2x2+ x3+ 3x4 ≤ 13 xi ≥ 0, xi є Z, i = 1,..,4. |
|
13) 3x1+ 7x2+ 7x3+ 5x4 → max
4x1+ 7x2+ 5x3+ 6x4 ≤ 13 xi ≥ 0, xi є Z, i = 1,..,4.
|
14) 2x1+ 4x2+ 5x3+ 6x4 → max
2x1+ 3x2+ 4x3+ 5x4 ≤ 14 xi ≥ 0, xi є Z, i = 1,..,4.
|
|
15) 5x1+ 6x2+ 3x3+ 4x4 → max
4x1+ 7x2+ 3x3+ 5x4 ≤ 18 xi ≥ 0, xi є Z, i = 1,..,4. |
16) 5x1+ 6x2+ 9x3+ 4x4 → max 4x1+ 5x2+ 8x3+ 3x4 ≤ 14 xi ≥ 0, xi є Z, i = 1,..,4. |
|
17) x1+ 7x2+ 3x3+ 8x4 → max
x1+ 4x2+ 2x3+ 5x4 ≤ 14 xi ≥ 0, xi є Z, i = 1,..,4. |
18) 9x1+ x2+ 2x3+5x4 → max
8x1+ x2+3x3+4x4 ≤ 15 xi ≥ 0, xi є Z, i = 1,..,4. |
|
19) 2x1+ 3x2+ 6 x3+9x4 → max
4x1+ 7x2+ 8x3+10x4 ≤ 20 xi ≥ 0, xi є Z, i = 1,..,4.
|
20) x1+ 8x2+ 9x3+7x4 → max
x1+ 5x2+ 8x3+ 6x4 ≤ 14 xi ≥ 0, xi є Z, i = 1,..,4.
|
|
21) 2x1+ 3x2+ 3x3+ 4x4 → max
4x1+ 4x2+ 5x3+ 5x4 ≤ 19 xi ≥ 0, xi є Z, i = 1,..,4. |
22) 4x1+ 3x2+ 7x3+ x4 → max 4x1+ 5x2+ 8x3+ 2x4 ≤ 14 xi ≥ 0, xi є Z, i = 1,..,4. |
|
23) x1+ 4x2+ 3x3+ 9x4 → max
x1+ 3x2+ 2x3+ 5x4 ≤ 17 xi ≥ 0, xi є Z, i = 1,..,4. |
24) 7x1+ x2+ 3x3+2x4 → max
6x1+ x2+2x3+3x4 ≤ 20 xi ≥ 0, xi є Z, i = 1,..,4. |
|
25) 2x1+ 3x2+ 6 x3+9x4 → max
4x1+ 7x2+ 8x3+10x4 ≤ 20 xi ≥ 0, xi є Z, i = 1,..,4.
|
26) x1+ 6x2+ 7x3+4x4 → max
x1+ 5x2+ 4x3+ 3x4 ≤ 19 xi ≥ 0, xi є Z, i = 1,..,4.
|
|
27) 2x1+ 5x2+ 3x3+ 7x4 → max
x1+ 3x2+ 2x3+ 5x4 ≤ 27 xi ≥ 0, xi є Z, i = 1,..,4. |
28) 5x1+ x2+ 3x3+7x4 → max
4x1+ x2+2x3+3x4 ≤ 26 xi ≥ 0, xi є Z, i = 1,..,4. |
|
29) 2x1+ 3x2+ 6 x3+7x4 → max
3x1+ 7x2+ 8x3+ 9x4 ≤ 25 xi ≥ 0, xi є Z, i = 1,..,4.
|
30) x1+ 6x2+ 4x3+4x4 → max
x1+ 5x2+ 4x3+ 3x4 ≤ 29 xi ≥ 0, xi є Z, i = 1,..,4.
|