Добавлен: 19.10.2018
Просмотров: 4048
Скачиваний: 59
СОДЕРЖАНИЕ
1.Исследование функции на безусловный экстремум
2. Численные методы безусловной минимизации
Метод конфигураций (Хука-Дживса)
Метод деформируемого многогранника (Нелдера-Мида)
Метод наискорейшего градиентного спуска
Метод сопряженных направлений (Флетчера – Ривса)
Порядок выполнения лабораторной работы
Пример выполнения лабораторной работы
3. Решение задачи минимизации со смешанными ограничениями
Седловые точки функции Лагранжа
Метод седловой точки в задачах квадратичного программирования
Метод проекции градиента для задачи условной оптимизации
Метод условного градиента для задачи условной оптимизации
Метод возможных направлений для задачи условной оптимизации
Порядок выполнения лабораторной работы
Пример выполнения лабораторной работы
4. Основные понятия линейного программирования
Модель задачи линейного программирования
Свойства задачи линейного программирования
Двойственность в линейном программировании
Построение модели транспортной задачи
Методы нахождения начального плана перевозок.
Задание 2. Числовые характеристики симметричной квадратной матрицы.
Задание 3. Формула Тейлора для функции нескольких переменных
Задание 4. Нахождение локальных экстремумов
Задание 5. Одномерная оптимизация
Задание 6. Многомерная оптимизация по направлению
Задание 7. Методы безусловной оптимизации
Задание 8. Методы условной оптимизации
Задание 9. Задача линейного программирования и симплекс-метод
Задание 10. Транспортная задача
(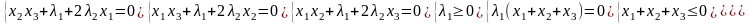 1′)
1′)
(2′)
(3′)
(4′)
(5′)
(6′)
(7′)
Если
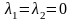 ,
то получаем точку
,
то получаем точку
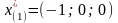 (из (1′)…(3′),(7′)).
(из (1′)…(3′),(7′)).
Остальные «симметричные» точки здесь и далее приводить не будем.
Если
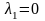 ,
,
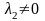 ,
,
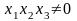 ,
то:
,
то:
(1′),(2′)
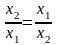
(2′),(3′)
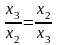
(7′)
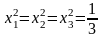
Из
(6′) получаем точки
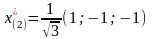 и
и
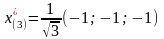 .
.
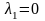 ,
,
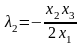 .
Для
.
Для
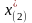 значение
значение
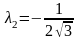 ,
для
,
для
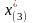 значение
значение
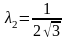 .
.
Если
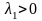 ,
,
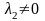 :
:
(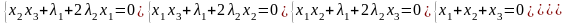 1′′)
1′′)
(2′′)
(3′′)
(4′′)
(5′′)
Если
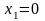 ,
то (2′′),(3′′)
,
то (2′′),(3′′) 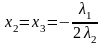 ;
(4′′)
;
(4′′) 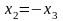 .
.
Следовательно,
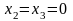 и
и
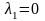 .
Но
.
Но
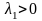 ,
пришли к противоречию.
,
пришли к противоречию.
Значит,
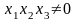 .
.
(1′′)+(2′′)+(3′′):
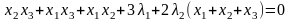
Последнее слагаемое равно нулю согласно (4′′).
Поэтому,
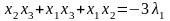 .
.
С
другой стороны,
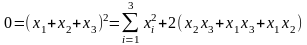
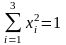 (по
(5′′))
(по
(5′′))
Следовательно,
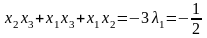
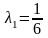 .
.
Если
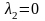 ,
то (1′′)…(3′′)
,
то (1′′)…(3′′) 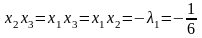 .
.
Разделим
на
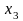 :
:
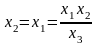 .
Но если
.
Но если
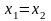 ,
то их произведение не может быть равно
,
то их произведение не может быть равно
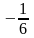 .
Значит,
.
Значит,
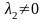 .
.
Если
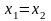 ,
получаем систему:
,
получаем систему:
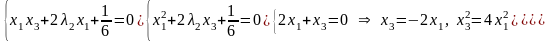
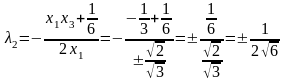
Получаем
точку
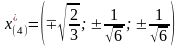 (в силу симметрии переменных
(в силу симметрии переменных
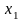 ,
,
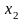 ,
,
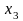 координаты можно переставить),
координаты можно переставить),
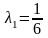 ,
,
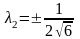 .
.
Предположив
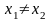 ,
получим те же результаты.
,
получим те же результаты.
Найдены следующие точки:
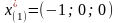 ,
,
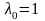 ,
,
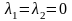 ;
;
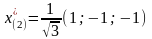 ,
,
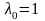 ,
,
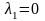 ,
,
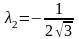 ;
;
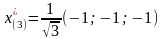 ,
,
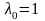 ,
,
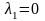 ,
,
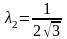 ;
;
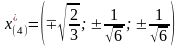 ,
,
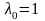 ,
,
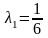 ,
,
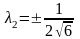 .
.
Запишем второй дифференциал обобщенной функции Лагранжа.
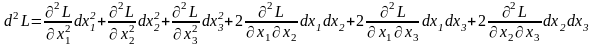
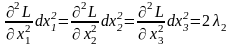
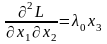 ,
,
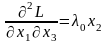 ,
,
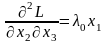
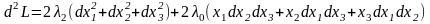
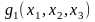 является
активным ограничением только для точки
является
активным ограничением только для точки
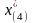 .
.
Применим достаточное условие минимума второго порядка к этой точке:
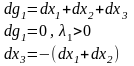
Подставив
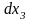 и
и
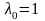 во второй дифференциал функции Лагранжа,
получим:
во второй дифференциал функции Лагранжа,
получим:
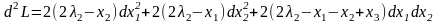
Запишем матрицу квадратичной формы относительно приращений:
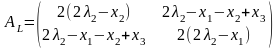
Для
«верхнего» знака
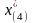 матрица
матрица
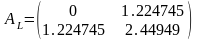 .
Для «нижнего» знака элементы матрицы
меняют знак. Согласно критерию Сильвестра,
в этой точке нет экстремума.
.
Для «нижнего» знака элементы матрицы
меняют знак. Согласно критерию Сильвестра,
в этой точке нет экстремума.
Сравним значения функции в остальных точках:
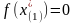
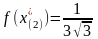
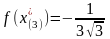
Точкой
глобального минимума является
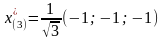 ,
значение функции в этой точке
,
значение функции в этой точке
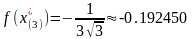 .
.
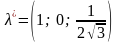
Проверим
справедливость оценки
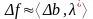 для точки
для точки
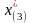 ,
,
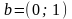 .
.
Возьмем
вектор
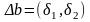 ,
ему соответствуют множители Лагранжа
,
ему соответствуют множители Лагранжа
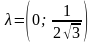 .
.
Следовательно,
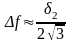 .
.
Перепишем
условие задачи, введя приращение
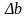 :
:
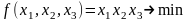
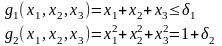
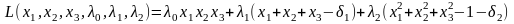
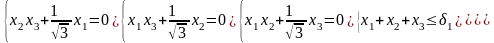
И з
первых трех уравнений получаем
з
первых трех уравнений получаем
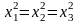 .
.
Подставим
в последнее уравнение:
 ,
,
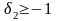 .
.
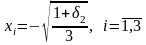 .
.
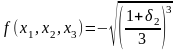 .
.
Возьмем,
например,
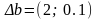 .
.
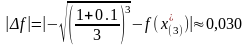 .
.
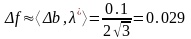
Проверим
для
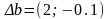 :
:
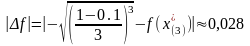
С
другой стороны,
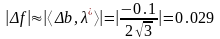 .
.
-
Решить задачу максимизации квадратичной функции

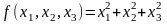 при условиях
при условиях
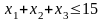 и
и
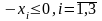 .
.
Решение.
Перепишем условие следующим образом:
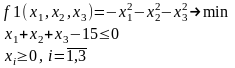
Функция Лагранжа имеет вид:
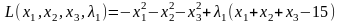
Необходимые и достаточные условия минимума:
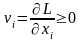
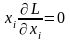
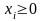
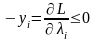
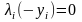
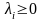
Получаем систему уравнений и неравенств:
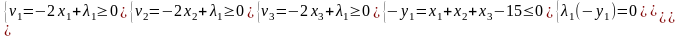
Для решения промежуточной задачи ЛП воспользуемся средствами MS Excel.
Введем формулы, соответствующие системе:
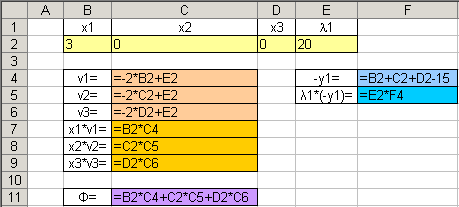
Зададим начальное приближение:
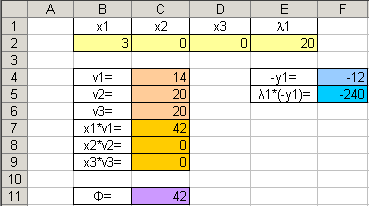
Заполним поля диалога «Поиск решения»:
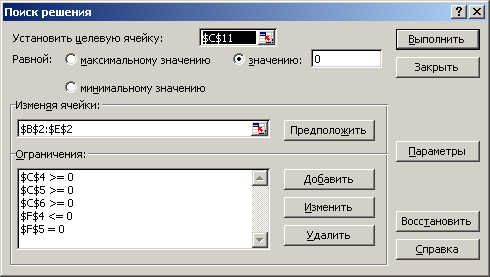
В окне «Параметры» установим флажок «Неотрицательные значения».
Результат поиска решения:
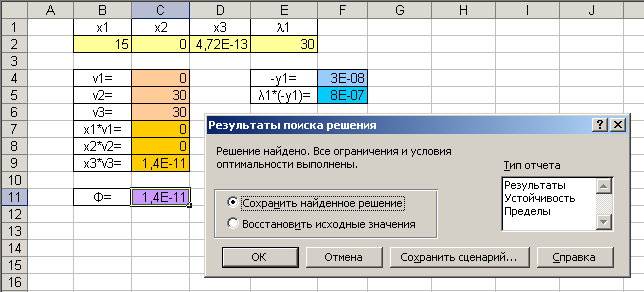
Найдена седловая точка функции Лагранжа: (х* ,λ*) = (15;0;0;30). Оптимальное решение задачи: х* (15;0;0), f(x*) = 152 = 225.
4. Основные понятия линейного программирования
Модель задачи линейного программирования
Линейное программирование – направление математики, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием оптимальности.
Математическая модель задачи линейного программирования (ЗЛП) включает в себя:
1)
целевую
функцию
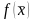 ,
оптимальное значение которой (максимум
или минимум) требуется отыскать:
,
оптимальное значение которой (максимум
или минимум) требуется отыскать:
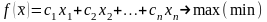 (1)
(1)
2) ограничения в виде системы линейных уравнений или неравенств (функциональные ограничения задачи):
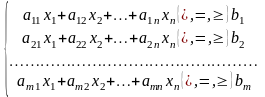 (2)
(2)
3) требование неотрицательности переменных (тривиальные ограничения задачи):
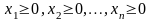 (3)
(3)
В
(1), (2), (3)
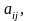
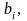
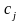 (
(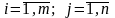 )
–
заданные постоянные величины.
)
–
заданные постоянные величины.
Задача состоит в нахождении оптимального значения функции (1) при соблюдении ограничений (2) и (3).
Вектор
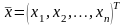 ,
удовлетворяющий ограничениям (2) и (3),
называется допустимым
решением
(планом)
ЗЛП.
,
удовлетворяющий ограничениям (2) и (3),
называется допустимым
решением
(планом)
ЗЛП.
План
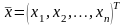 ,
имеющий не более m
компонентов, отличных от нуля, называется
допустимым
базисным планом
ЗЛП.
,
имеющий не более m
компонентов, отличных от нуля, называется
допустимым
базисным планом
ЗЛП.
План
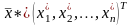 ,
при котором целевая функция
,
при котором целевая функция
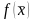 достигает максимального (минимального)
значения, называется оптимальным.
достигает максимального (минимального)
значения, называется оптимальным.
Итого, математическая модель ЗЛП в векторно-матричной форме принимает вид:
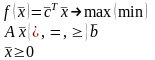 ,
,
где
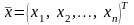 –
оптимизируемый вектор параметров;
–
оптимизируемый вектор параметров;
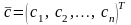 –
целевой вектор;
–
целевой вектор;
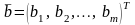 –
вектор
ограничений;
–
вектор
ограничений;
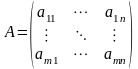 –
технологическая
матрица.
–
технологическая
матрица.
Свойства задачи линейного программирования
Рассмотрим некоторые теоремы (без доказательства), отражающие фундаментальные свойства ЗЛП и лежащие в основе методов их решения.
Теорема. Множество всех планов ЗЛП выпукло (если оно не пусто).
Таким образом, множество всех решений ЗЛП является выпуклым многогранником (многогранником решений).
Теорема. Целевая функция ЗЛП достигает своего максимального (минимального) значения в угловой точке многогранника решений. Если целевая функция принимает минимальное (максимальное) значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.
Итак, если целевая функция ЗЛП ограничена на многограннике решений, то существует такая угловая точка многогранника решений, в которой линейная функция ЗЛП достигает своего оптимума.
Теорема. Каждый допустимый базисный план является угловой точкой множества допустимых планов.
Теорема.
Если
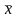 – угловая точка множества допустимых
планов, то она является допустимым
базисным планом задачи.
– угловая точка множества допустимых
планов, то она является допустимым
базисным планом задачи.
Двойственность в линейном программировании
С каждой задачей линейного программирования можно связать двойственную задачу.
Рассмотрим ЗЛП в стандартной форме (прямую задачу):
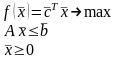
Задача
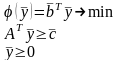
называется двойственной к прямой задаче.
Сравнивая прямую задачу и двойственную, можно заметить пять «зеркальных» соотношений между ними:
1) число переменных прямой задачи равно числу функциональных ограничений двойственной задачи и наоборот;
2) технологические матрицы транспонированы по отношению друг к другу;
3) целевой
вектор
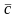 прямой задачи равен вектору ограничений
двойственной задачи и наоборот;
прямой задачи равен вектору ограничений
двойственной задачи и наоборот;
4) направления оптимизации противоположны;
5) знаки неравенств в функциональных ограничениях противоположны.
Если
система функциональных ограничений
прямой задачи состоит из неравенств и
на все переменные
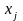 наложено
условие неотрицательности, то прямая
и двойственная задачи образуют
симметричную
пару двойственных задач.
В противном случае, прямая и двойственная
задачи образуют несимметричную
пару двойственных задач.
наложено
условие неотрицательности, то прямая
и двойственная задачи образуют
симметричную
пару двойственных задач.
В противном случае, прямая и двойственная
задачи образуют несимметричную
пару двойственных задач.
В
несимметричном случае двойственная
задача составляется по тем же правилам,
что и в случае симметричной пары, но
если
функциональное ограничение прямой
задачи является равенством, то
соответствующая неизвестная двойственной
задачи может принимать как положительные,
так и отрицательные значения и наоборот.
Более того, если в прямой задаче переменная
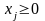 , то
соответствующее j-ое
ограничение двойственной задачи –
неравенство вида «
, то
соответствующее j-ое
ограничение двойственной задачи –
неравенство вида «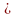 »,
если двойственная задача решается на
минимум, и «
»,
если двойственная задача решается на
минимум, и «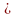 »,
если на максимум.
»,
если на максимум.
Смысл теории двойственности раскрывается с помощью двух теорем, из которых первая является основной, а вторая является следствием из первой. Нас в дальнейшем будет интересовать только первая теорема.
Теорема (Первая теорема двойственности).
I.
Если одна из задач двойственной пары
имеет решение, то и другая имеет решение,
причём экстремальные значения целевых
функций совпадают:
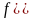 .
.
II. Если одна из задач не имеет решения из-за неограниченности целевой функции, то другая также не имеет решения из-за противоречивости условий и наоборот.
Замечание.
Для первой теоремы двойственности
справедливо обращение: если
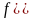 ,
то планы
,
то планы
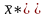 и
и
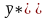 –
оптимальные.
–
оптимальные.
5. Задача транспортного типа
Построение модели транспортной задачи
Под транспортной задачей (ТЗ) обычно понимают задачу выбора плана перевозок некоторого товара от m источников (пунктов производства, поставщиков) к n стокам (станциям назначения, пунктам сбыта), обеспечивающего минимальные транспортные затраты. При этом предполагают, что а) мощность i-го источника равна Si>0, i=1, ..., m; б) мощность j-го стока равна Dj>0, j=1,...,n; в) стоимость перевозки единицы товара от i-го источника к j-му стоку (тариф) равна cij (в условных денежных единицах).
Для математического описания транспортной задачи вводятся переменные хij, обозначающие объемы поставок товара из i-го источника к j-му стоку (в условных единицах объема товара ).
Таким образом, получаем модель ТЗ в виде задачи линейного программирования
ΣΣckjxkj→ min; (1)
Σхij= Si, (i=1,...,m);
Σхij= Dj, (j=1,..., n); (2)
xij≥0, i=1,...,m, j=1,..., n
Задача (1) с ограничениями (2) может быть решена стандартным симплекс-методом. Однако, специфика ограничений (каждое неизвестное входит только в два уравнения системы (2) с коэффициентами, равными 1) позволяет разработать специальные методы решения ТЗ и задач, которые сводятся к задачам транспортного типа (задача о назначениях, задача выбора кратчайшего пути, задача о замене оборудования и т.п.).
Формы представления ТЗ.
Задача (1), (2) может быть представлена в виде так называемой транспортной таблицы (матричная форма) (Рис.1 ) или в виде сети с ориентированными ребрами (Рис.2). Узлы сети соответствуют источникам и стокам ТЗ, ребро, соединяющее узлы i и j, – доставке товара из i-го источника к j-му стоку. Для каждого узла указывается его мощность, для каждого ребра – стоимость доставки груза (тариф).
Систему уравнений (2) можно представить в эквивалентном виде
Σхij= Si, (i=1,...,m);
-Σхij= -Dj, (j=1,..., n); (2’)
Тогда для представления задачи (1), (2’) удобнее использовать следующую форму транспортной таблицы (Рис. 3). Свободные места в таблице соответствуют нулевым коэффициентам при соответствующих переменных. Источникам соответствуют коэффициенты 1, а стокам - коэффициенты -1. В сетевой форме этой записи задачи будут соответствовать мощности стоков, равные (–Dj ).
|
сток источник |
1 |
… |
j |
… |
n |
поставки |
|
1 |
x11 c11 |
… |
x1j c1j |
… |
x1n c1n |
S1 |
|
… |
… |
… |
… |
… |
… |
… |
|
i |
xi1 ci1 |
… |
xij cij |
… |
xin cin |
Si |
|
… |
… |
… |
… |
… |
… |
… |
|
m |
xm1 cm1 |
… |
xmj cmj |
… |
xmn cmn |
Sm |
|
|
|
… |
|
… |
|
|
|
спрос |
D1 |
… |
Dj |
… |
Dn |
|
Рис.1

c23
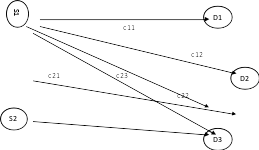
Рис.2.
|
|
|
Объем поставок |
|
|
|||||
|
|
|
x11 x12 ...x1n |
x21 x22 ...x2n |
... |
xm1 xm2 ...xmn |
|
|||
|
Поставки |
1 2 … m |
1 1 … 1 |
1 1 … 1 |
… |
1 1 … 1 |
S1 S2 ,,, Sm |
|||
|
спрос |
1 2 ... n |
-1 -1 … -1 |
-1 -1 … -1 |
… |
-1 -1 … -1 |
-D1 -D2 ... -Dn |
|||
|
|
|
c11 c12 ...c1n |
c21 c22 ...c2n |
... |
cm1 cm2 ...cmn |
|
|||