Добавлен: 19.10.2018
Просмотров: 3277
Скачиваний: 7

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Институт горного дела и строительства
Кафедра ССМиК
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ
КУРСОВОЙ РАБОТЫ №1
по дисциплине
ИНФОРМАТИКА
Тема «Численные методы решения нелинейных уравнений»
Уровень профессионального образования: высшее образование – бакалавриат
Направление подготовки: 08.03.01
«Строительство»
Профиль подготовки:
«Промышленное и гражданское строительство»
«Городское строительство и хозяйство»
Квалификация выпускника: бакалавр
Форма обучения: заочная
Тула 2015

Рассмотрено на заседании кафедры
протокол № от « » 20 г.
Зав. кафедрой А.А.Трещев

1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Сегодня компьютер обычно воспринимается как техническое офисное
средство, инструмент для работы в Internet или игровая приставка. Вместе с
тем, изначально само его название (от англ. computer — вычислитель) указывает,
что по своей природе этот инструмент предназначен в первую очередь для вы-
полнения различного рода расчетов.
Компьютер не только обеспечивает автоматизацию процесса вычислений,
но и позволяет применять для решения задач специальные численные методы,
которые практически не могут использоваться без его поддержки.
Данные методы называются численными потому, что они основаны на
операциях с числами, то есть на четырех арифметических действиях - сло-
жении, вычитании, умножении и делении, но позволяют решать разного вида
уравнения, включая дифференциальные, производить интегрирование функций,
решать задачи оптимизации и т. п.
1.1. Нелинейные уравнения
Довольно часто в инженерной практике встречаются задачи, связанные с
необходимостью отыскания корней нелинейных уравнений. Такие задачи
обычно возникают как элементарные составляющие при решении различных
технических и научных проблем.
1.1.1. Постановка задачи
Рассмотрим в качестве примера процедуру выбора рабочего режима
транзисторного усилительного каскада. Предположим, что зависимость ко-
эффициента усиления каскада от тока эмиттера транзистора i
э
может быть пред-
ставлена формулой
5
5
4
4
3
3
2
2
1
0
)
(
э
э
э
э
э
э
i
a
i
a
i
a
i
a
i
а
а
i
K
где a
0
, a
1
, a
2
, a
3
, a
4
, a
5
- известные постоянные. Если необходимо, чтобы
транзистор обеспечивал требуемый коэффициент усиления K
тр
, то рабочий ток
i
э
должен выбираться таким образом, чтобы выполнялось равенство
K(i
э
)= К
тр
или
тр
э
э
э
э
э
K
i
a
i
a
i
a
i
a
i
а
а
5
5
4
4
3
3
2
2
1
0
Последняя запись по сути дела является уравнением, которое можно пред-
ставить в следующем виде:
0
5
5
4
4
3
3
2
2
1
0
тр
э
э
э
э
э
K
i
a
i
a
i
a
i
a
i
а
а
Решение этого уравнения и дает искомое значение тока i
э
.

Как видно, задача выбора эмиттерного тока транзистора свелась к ре-
шению уравнения вида
f(x) = 0, (1)
где роль неизвестного x играет ток i
э
, аf(x) является некоторой функцией этого
неизвестного. Подобным же образом к решению уравнения могут быть сведены
многие проектные и исследовательские задачи, в которых необходимо найти
значение какого-либо параметра по известной зависимости.
Следует отметить, что обычно характеристики реальных технических
устройств зависят не от одного, а от нескольких параметров. В этом случае
проблема выбора параметров приводит к необходимости решения системы
уравнений со многими неизвестными. Примером такого рода задачи является
выбор сопротивлений резисторов в схеме многокаскадного усилителя. Однако
далее мы будем рассматривать только задачи, связанные с решением одного
нелинейного уравнения с одним неизвестным.
1.1.2. Виды нелинейных уравнений
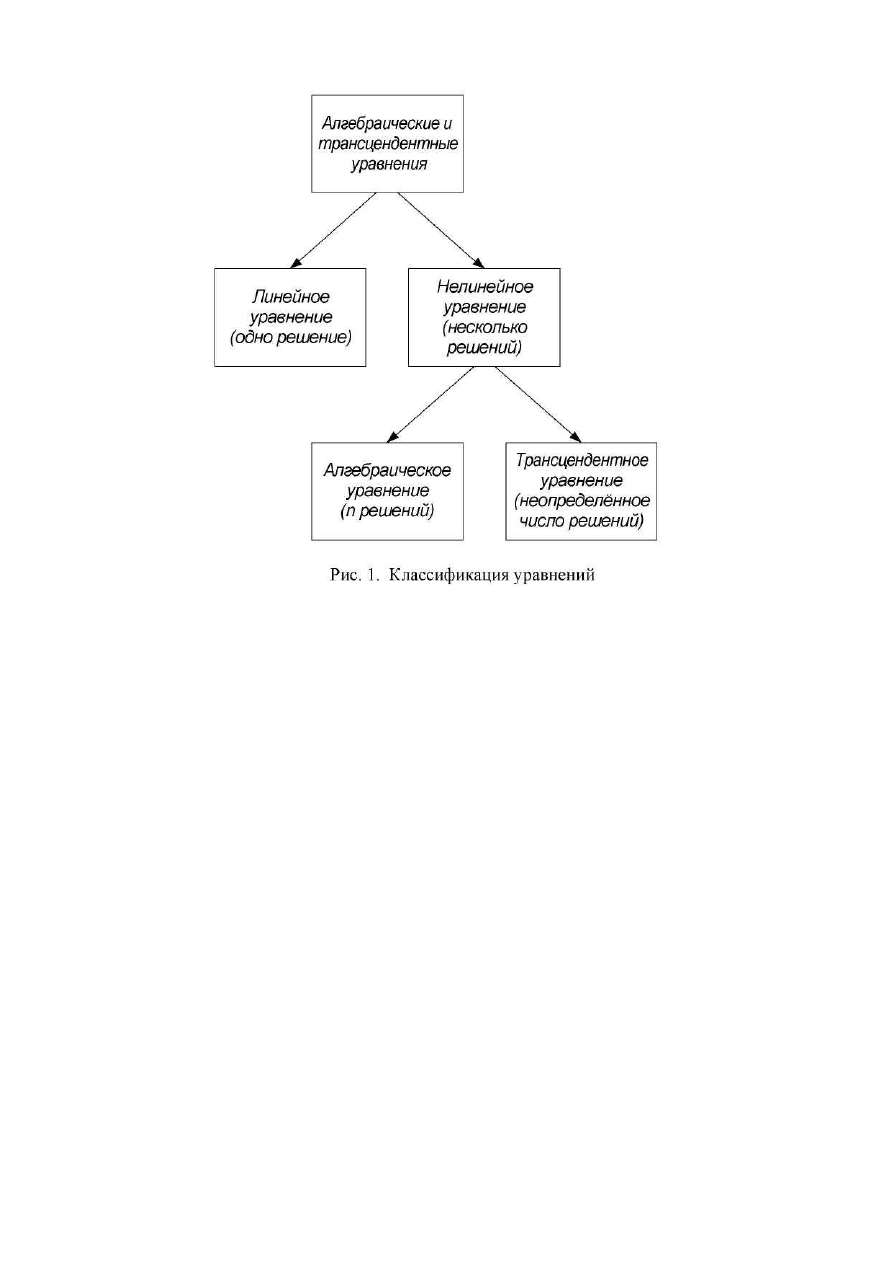
Очевидно, что способ решения уравнения определяется его видом. В
математике принято подразделять нелинейные уравнения на алгебраические и
трансцендентные (см. рис. 1).
К алгебраическим относят уравнения, в которых функцияf(x) является
степенным многочленом, то есть:
0
...
4
4
3
3
2
2
1
0
n
n
x
a
x
a
x
a
x
a
x
а
а
(2)
где a
0
, a
1
, a
2
, a
3
, a
4
, ... , a
n
- коэффициенты, а n - целое число, соответствующее
максимальной степени многочлена. Подобное уравнение было рассмотрено
выше.
К трансцендентным относят уравнения, содержащие трансцендентные
функции, то есть показательную, логарифмическую, тригонометрические
функции.
Например, трансцендентными являются следующие уравнения:
0
4
,
0
1
3
,
0
1
1
,
2
)
2
sin(
2
x
x
x
x
(3)
0
)
sin(
5
,
5
)
44
lg(
6
2
1
,
0
x
x
x
(4)
Свойства алгебраических и трансцендентных уравнений существенно
различаются. Поэтому различны и подходы к их решению.
Для алгебраических уравнений до четвертого порядка включительно из-
вестны прямые точные методы решения. Кроме того, количество корней можно
определить по степени многочлена, а их характер по знакам коэффициентов
этого многочлена.
Для трансцендентных уравнений общих приемов решения кроме при-
ближенных не существует. Количество корней такого уравнения обычно не-
возможно определить заранее по его виду. Трансцендентное уравнение может
не иметь ни одного вещественного корня, иметь счетное количество корней или
бесконечное множество корней. Из двух приведенных выше уравнений первое
имеет семь вещественных корней, а второе - пять корней (попробуйте опреде-
лить их самостоятельно).
1.1.3. Методы решения уравнений
К сожалению, во многих практически важных случаях, когда уравнение
имеет сложный вид, аналитически его точное решение найти не удается. От-
сутствуют методы решения в общем виде алгебраических уравнений высоких
степеней. Для трансцендентных уравнений точное решение найти можно в не-
многих самых простых случаях.
Если решение нельзя найти в явном виде, то для отыскания корня ис-
пользуют другие методы. Например, приближенное решение можно получить
методом последовательных приближений. Сравнительно легко (но и весьма
неточно) корни уравнения определяются графически - достаточно лишь для