ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5529
Скачиваний: 27
56
таких способов размещения равно
.
r
n
P
=
В частном случае, когда каждая ячейка может содержать
только один элемент,
!
!
)
1
)...(
1
(
r
n
n
r
n
n
n
P
−
=
+
−
−
=
.
Число способов размещения
n
одинаковых объектов по
r
различным ячейкам. Возможны две разновидности задач этого
класса:
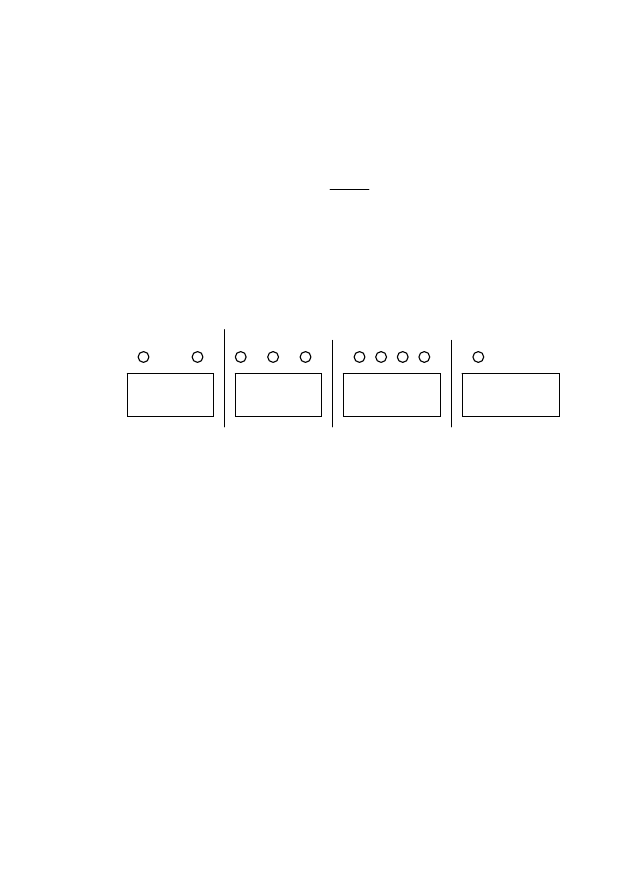
а) Ни одна ячейка не пуста (рис. 3.1). Задача состоит в нахож-
дении числа способов провести
1
−
r
линий в
1
−
n
промежутках.
Это число равно
).
1
,
1
(
−
− r
n
C
Рис.3.1 – Задача о размещениях
Варианты задачи: число способов окрашивания
r
цветами
n
одинаковых объектов; число
r
- сочетаний с повторениями, в кото-
рых каждый элемент использован.
б) Ячейки могут быть пустыми. В этом случае к множеству
элементов присоединяют
r
символических «пустых элементов».
Задача сводится к определению числа способов провести
1
−
r
ли-
ний в
1
−
+ r
n
промежутках между элементами. Число таких спо-
собов равно
).
1
,
(
−
+ r
n
n
C
К этой разновидности относится, на-
пример, задача нахождения числа решений уравнения
n
x
x
x
r
=
+
+
+
...
2
1
в неотрицательных числах.
Решение задач третьего и четвертого классов представляет
значительно большие трудности, однако возможно в ряде простей-
ших случаев.

57
3.6.
Производящие
функции
До сих пор мы занимались прямыми, или «элементарными»,
методами подсчета количества комбинаторных конфигураций. Про-
изводящие функции представляют собой аппарат для реализации
косвенных методов подсчета количества комбинаторных конфигу-
раций.
Метод производящих функций является одним из самых разви-
тых и самых сильных в приложениях методов комбинаторного ана-
лиза. Основные идеи этого метода впервые были высказаны в конце
XVIII века в работах Лапласа по теории вероятностей.
Поясним идею метода на примерах производящих функций для
сочетаний и перестановок.
Производящие функции для сочетаний. Для примера рас-
смотрим три объекта, обозначив их
3
2
1
,
,
x
x
x
, образуем произведе-
ние
).
1
)(
1
)(
1
(
3
2
1
t
x
t
x
t
x
+
+
+
Раскрыв скобки и расположив полином по степеням
t
, полу-
чим
t
x
x
x
t
x
x
x
x
x
x
t
x
x
x
3
2
1
2
3
2
3
1
2
1
3
2
1
)
(
)
(
1
+
+
+
+
+
+
+
или
∑
=
=
+
+
+
3
0
3
2
1
3
3
2
2
1
,
)
,
,
(
1
r
r
r
t
x
x
x
a
t
a
t
a
t
a
где
3
2
1
,
,
a
a
a
- элементарные симметрические функции трех
переменных
.
,
,
3
2
1
x
x
x
Очевидно, что число слагаемых каждого
коэффициента
)
3
,
2
,
1
(
=
r
a
r
равно
).
,
3
( r
C
Следовательно, при
)
3
,
2
,
1
(
1
=
= i
x
i
получим
∑
∑
=
=
=
=
+
3
0
3
0
3
)
,
3
(
)
1
,
1
,
1
(
)
1
(
r
r
r
r
r
t
r
C
t
a
t
Для
n
различных объектов
n
x
x
x
,...,
,
2
1
будем иметь

58
∑
∑
∑
=
=
=
=
=
=
+
=
+
Π
n
r
n
r
r
r
r
n
n
r
r
n
r
r
n
r
t
r
n
C
t
a
t
t
x
x
a
t
x
0
0
0
1
1
.
)
,
(
)
1
,...,
1
(
)
1
(
,
)
,...,
(
)
1
(
(13)
Функцию
n
t
t
f
)
1
(
)
(
+
=
называют (обычной) производящей
функцией сочетаний из
n
различных объектов.
Придавая в (13) различные частные значения переменной
t
,
получим некоторые интересные соотношения:
).
,
(
)
1
(
...
)
3
,
(
)
2
,
(
1
)
,
(
)
1
(
0
:
1
),
,
(
...
)
3
,
(
)
2
,
(
1
)
,
(
2
:
1
0
0
n
n
C
n
C
n
C
n
r
n
C
t
n
n
C
n
C
n
C
n
r
n
C
t
n
n
r
r
n
r
n
−
+
+
+
−
+
−
=
−
=
−
=
+
+
+
+
+
=
=
=
∑
∑
=
=
Почленное сложение и вычитание этих равенств дает
∑
∑
=
−
−
=
+
=
n
r
n
r
n
r
n
C
r
n
C
0
0
1
,
2
)
1
2
,
(
)
2
,
(
а простая разбивка сомножителей
m
m
n
n
t
t
t
)
1
(
)
1
(
)
1
(
+
+
=
+
−
и приравнивание коэффициентов при
r
t
приводят к равенству
)
0
,
(
)
,
(
...
)
1
,
(
)
1
,
(
)
,
(
)
0
,
(
)
,
(
m
C
r
m
n
C
r
m
C
m
n
C
r
m
C
m
n
C
r
n
C
−
+
+
−
−
+
−
=
или
∑
=
−
−
=
r
K
k
r
m
C
k
m
n
C
r
n
C
0
).
,
(
)
,
(
)
,
(
Пример 1.
Найти производящую функцию для
r
-сочетаний с
ограниченным числом повторений из
n
элементов.
Здесь нельзя воспользоваться произведением биномов вида
t
x
k
+
1
, как для
r
-сочетаний без повторений, так как всякий такой

59
бином отражает лишь две возможности: элемент
k
x
множества либо
не появляется в
r
-сочетании, либо появляется в нем один раз. Пусть
k
x
появляется в
r
-сочетаниях с повторениями
j
,...,
2
,
1
,
0
раз. То-
гда ровно
i
появлениям элемента
k
x
соответствует одночлен
,
i
k
i
k
t
x
а по обобщенному правилу суммы появлениям элемента
k
x
”либо 0, либо 1,…, либо
j
раз“ соответствует полином
j
j
k
k
k
t
x
t
x
t
x
+
+
+
+
...
1
2
2
и значит производящая функция в этом случае имеет вид
).
...
1
(
)
(
2
2
1
j
j
K
K
K
n
K
t
x
t
x
t
x
t
F
+
+
+
+
Π
=
=
Если в этой задаче важен не вид производящей функции, а чис-
ло
соответствующих
r
-сочетаний,
то
принимаем
1
...
2
1
=
=
=
=
n
x
x
x
и представляем производящую функцию в
виде
∑
=
=
+
+
+
+
n
r
r
r
n
j
t
a
t
t
t
0
2
.
)
...
1
(
Пример 2.
Найти производящую функцию для
r
-сочетаний с
неограниченным числом повторений из
n
-элементов.
Построим эту функцию на основе предыдущего примера при
:
,...
2
,
1
,
0
=
j
∑
∑
∑
∑
∞
=
∞
=
∞
=
∞
=
−
−
+
=
−
+
+
=
−
+
−
−
−
−
−
=
−
−
=
−
=
−
=
+
+
+
=
0
0
0
0
2
,
)
,
1
(
!
)
1
)...(
1
(
)
1
(
!
)
1
)...(
1
)(
(
)
)(
,
(
)
1
(
)
1
1
(
...)
1
(
)
(
r
r
r
r
r
r
r
r
r
n
n
n
t
r
r
n
C
t
r
r
n
n
n
t
r
r
n
n
n
t
r
n
C
n
t
t
t
t
f
откуда
имеем
последовательность
,...
1
,
0
),
2
,
1
(
...},
,
{
1
0
=
−
+
=
r
r
n
C
a
a
a
r
чисел
r
-сочетаний с
60
повторениями из
n
элементов. Этот результат согласуется с полу-
ченным ранее.
Производящие функции для перестановок. По определению
в случае
n
различных элементов число сочетаний равно
.
!
)
,
(
)
,
(
r
r
n
P
r
n
C
=
Поэтому из (13) следует, что
∑
=
=
+
n
r
r
n
r
t
r
n
P
t
0
,
!
)
,
(
)
1
(
(14)
т.е. число перестановок
)
,
(
r
n
P
есть коэффициент при
!
r
t
r
.
Это и есть (экспоненциальная) производящая функция для числа
r
-
перестановок.
При возможности неограниченного повторения элементов не-
обходимо в левой части равенства (14) бином
t
+
1
заменить на ряд
вида
...
!
3
!
2
!
1
1
3
2
+
+
+
+
t
t
t
.
В случае, если соответствующий элемент допускает
l
K
K
K
,...
,
2
1
повторений в выборках в выборках, бином следует
заменить выражением
.
!
...
!
!
2
1
2
1
l
Kl
K
K
K
t
K
t
K
t
+
+
+
Представление соответствующего произведения в виде поли-
нома по степеням
t
дает в качестве коэфффициентов при
!
r
t
r
числа
r
-перестановок, допускающих указанные повторения.
Производящие функции для упорядоченных выборок называ-
ются экспоненциальными в силу того, что для
r
-перестановок с
неограниченным числом повторений из
n
элементов производящая
функция имеет вид степени ряда для функции
:
t
e