Файл: Лабораторной работы 2.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 24.10.2023

Просмотров: 50

Скачиваний: 7

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


Лабораторной работы № 2


«Исследование распределения магнитного поля, образованного прямым и круговым токами»

Цель работы:

  • Ознакомление с методикой измерения индукции магнитного поля.

  • Экспериментальное исследование магнитного поля, созданного прямым и круговым токами.

  • Приобретение навыков расчета магнитного поля с помощью закона Био – Савара – Лапласа.

Краткое теоретическое содержание работы:

Индукция магнитного поля 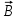– векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой 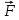магнитное поле действует на заряд 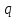, движущийся со скоростью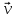

Схема установки

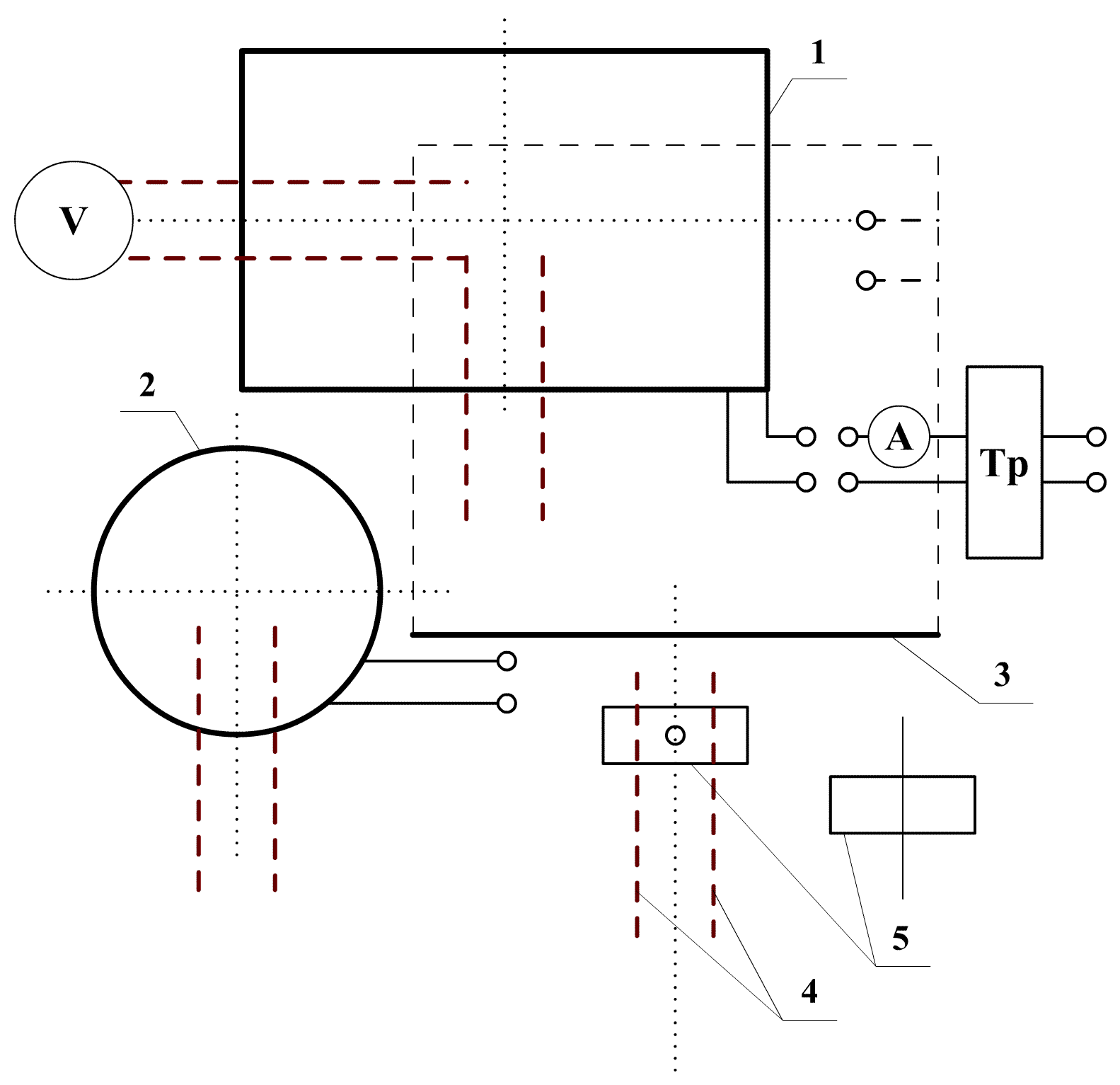
Рис. 1. Схема экспериментальной установки

Обозначения:

1 – прямоугольный контур;

2 – круговой контур;

3 – отрезок прямолинейного проводника;

4 – гнезда;

5 – штепсельная вилка;

А – амперметр;

V – вольтметр;

Тр – питающий трансформатор.
Метод измерения индукции магнитного поля основан на использовании явления электромагнитной индукции. Через проводники пропускают переменный ток, в результате чего в окружающем эти проводники пространстве образуется переменное магнитное поле.
Расчётные формулы

1. При измерениях:



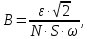
где 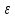– действующее значение ЭДС, индуцируемой в измерительной катушке;

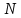– число витков измерительной катушки;


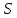– площадь витка измерительной катушки;

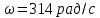– циклическая частота переменного тока.

2. Для вычисления значений индукции магнитного поля от отрезка прямого тока применяется формула:



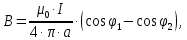
где 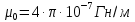– магнитная постоянная;

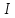– ток, протекающий по проводнику;

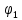– угол, образованный осью проводника и прямой, соединяющей начало отрезка прямого тока и точку, в которой определяется магнитная индукция;

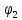– угол, образованный осью проводника и прямой, соединяющей конец отрезка прямого тока и точку, в которой определяется магнитная индукция;

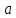– расстояние от прямолинейного отрезка проводника с током до точки, в которой определяется магнитная индукция

3.Для вычисления значений индукции магнитного поля в центре кругового контура применяется формула:



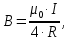
где 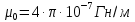– магнитная постоянная;

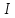– ток, протекающий по проводнику;

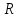– радиус проводника с токо

Результаты измерений
1. Для кругового контура

Таблица 1



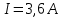
r (см)
1
2
3
4
6
7
8
9
10

ε (мВ)
5,7
9,8
19,8
50,5
104,1
66,5
54,3
49,3
48,8

B (мТл)
0,33
0,57
1,16
2,96
6,09
3,89
3,18
2,88
2,86

2. Для отрезка прямого тока

Таблица 2




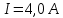
r (см)
1
2
3
4
5
6

ε (В)
48,1
22,8
13,8
9,3
6,3
4,3

B (Тл)
2,81
1,33
0,81
0,54
0,37
0,25


Обработка результатов

1. Графические зависимости
B = f(r) (по данным таблицы 1)


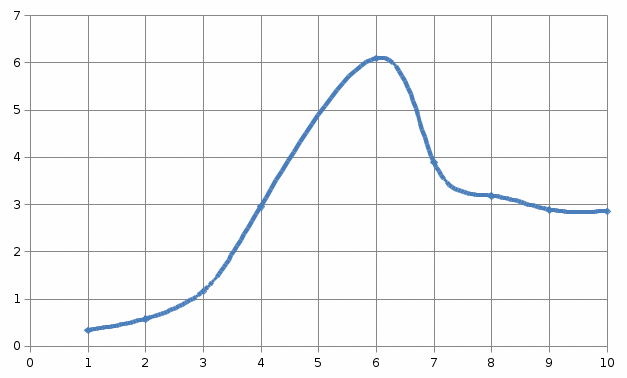
Рис. 2. График зависимости 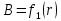для кругового контура

B = f(r) (по данным таблицы 2)


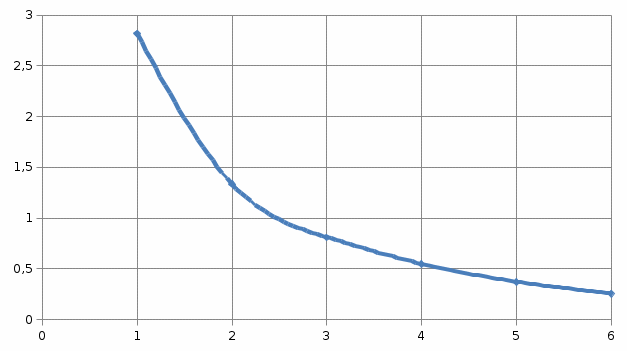
Рис. 3. График зависимости 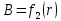для отрезка прямого тока
2.Сравните экспериментальные данные с расчётными:


Круговой контур

Экспериментальное значение в
в центре контура, мТл
Расчётное значение в
в центре контура, мТл

4,97
6,09



Отрезок прямого тока

Расстояние от катушки
до проводника (см)
Экспериментальное
значение B
Расчётное
значение B

1
2,81
2,22

2
1,33
1,09

3
0,81
0,70

4
0,54
0,50

5
0,37
0,38

6
0,25
0,30



Выводы:

1. Ознакомились с методикой измерения индукции магнитного поля.

2. Экспериментальное исследовали магнитное поле, созданное прямым и круговым токами.

3. Приобрели навыки расчета магнитного поля с помощью закона Био – Савара – Лапласа.

4. Зависимость индукции магнитного поля 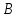от расстояния 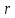от измерительной катушки до центра кругового контура имеет четко выраженный максимум, соответствующий точке, соответствующей центру контура.

5. Зависимость индукции магнитного поля
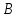
от расстояния от измерительной катушки до проводника с током для отрезка прямого тока имеет монотонно убывающий характер.

6. Сравнение экспериментальных данных с результатами, полученными расчетным путем, показывает достаточное (погрешность не превышает 20 %) их соответствие друг другу.

Смотрите также файлы