Добавлен: 24.10.2023
Просмотров: 47
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
№10 Задача 1 (формулировка полностью):
Найти модуль и главное значение аргумента комплексных чисел, записать это число в тригонометрической и показательной формах.
.Решение:
Комплексное число задано в алгебраической форме записи:
,где
– действительная часть;
– мнимая часть.Изобразим это число на комплексной плоскости.
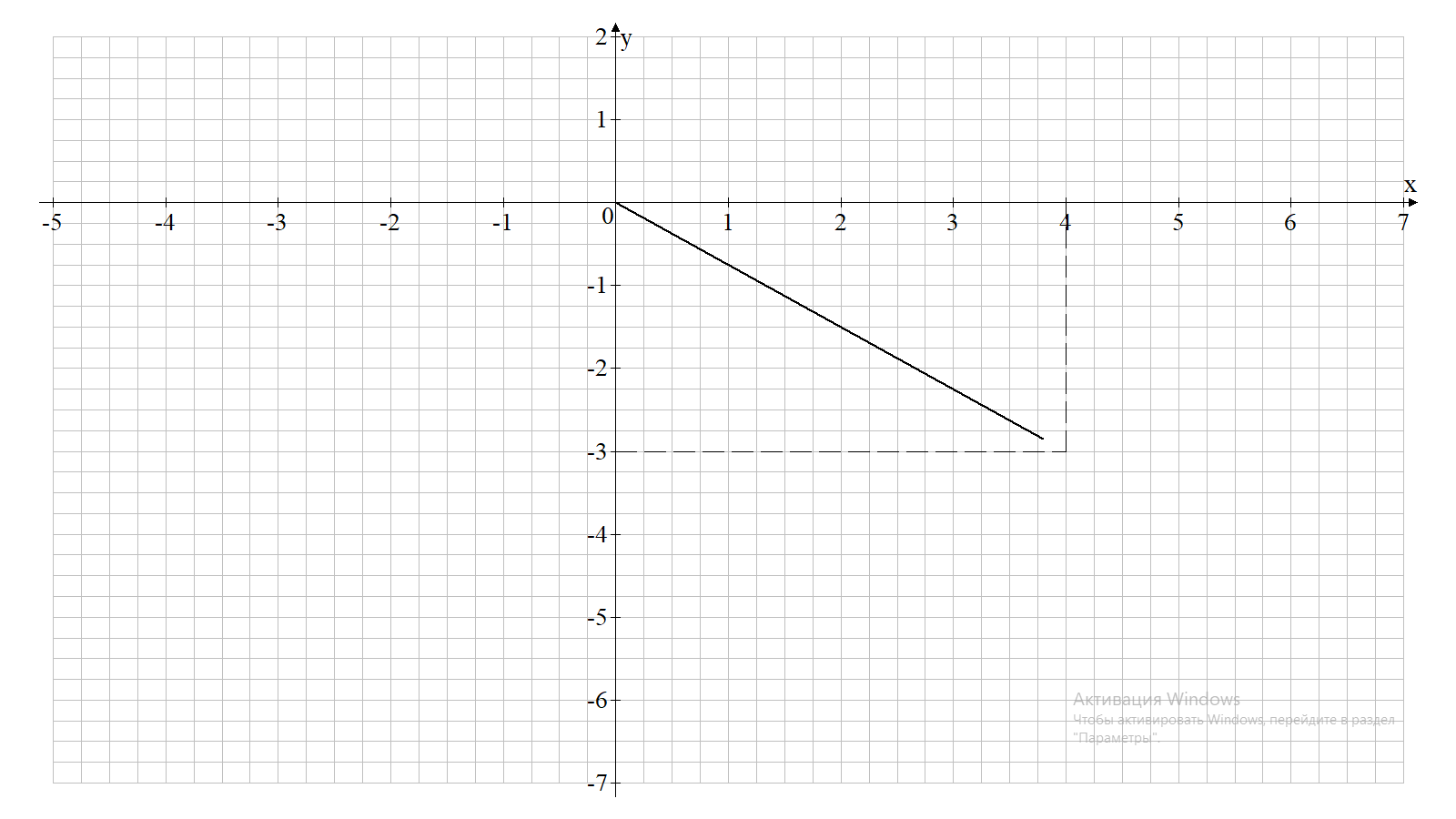
Найдём модуль комплексного числа:
.Найдём аргумент комплексного числа (
):
рад.Запишем комплексное число в тригонометрической форме:
.Запишем комплексное число в показательной форме:
.Ответ:
, 
, 
.№11 Задача 2 (формулировка полностью):
Вычислите.
а)
;б)
.Решение:
а)
.Избавимся от комплексного знаменателя в дроби:
;
.Найдём модуль и аргумент числа
и запишем его в тригонометрической форме:
;
;
рад;
.Возведём полученное число в степень, используя формулу Муавра:
Или в алгебраической форме:
.б)
.Преобразуем заданное выражение:
.Найдём модуль и аргумент числа
и запишем его в тригонометрической форме:
;
.Корень n-й степени из комплексного числа, заданного в тригонометрической форме
, находится по формуле:
, где 
.Найдём заданные корни:
;при k = 0 получаем:
;при k = 1 получаем:
при k = 2 получаем:
Ответ:_а)'>Ответ:
а)
;б)
;
;
.№12 Задача 3 (формулировка полностью):
Найдите значение действительной и мнимой частей функции.
.Решение:
Приведём функцию к виду
(учтём, что 
, 
):
Таким образом:
– действительная часть функции;
– мнимая часть функции.Ответ:
, 
.№13 Задача 4 (формулировка полностью):
Дана функция
. Найти значение функции при заданном значении z.
.Решение:
Вычислим значение функции при заданном значении z:
, 
;
;
.Ответ:
.№14 Задача 5 (формулировка полностью):
Найти Ln z.
.Решение:
Определим модуль r и аргумент φ комплексного числа:
;
;
рад.Запишем логарифм комплексного числа:
;
.Ответ:
.№15 Задача 6 (формулировка полностью):
Пользуясь условиями Коши – Римана, выяснить, является ли функция
дифференцируемой хотя бы в одной точке.
.Решение:
Приведём функцию к виду
(учтём, что 
, 
):
;
– действительная часть функции;
– мнимая часть функции.Найдём частные производные от функций u(x; y) и v(x; y):
Проверим, выполняются ли условия Коши-Римана:
;
.Заметим, что первое условие не выполняется ни при каких значениях x и y. Следовательно, функция ω(z) не является дифференцируемой ни в одной из точек.
Ответ: функция ω(z) не является дифференцируемой ни в одной из точек.