Добавлен: 20.10.2018
Просмотров: 1494
Скачиваний: 4

n
j
k
j
n
k
jk
k
j
n
j
j
j
x
x
R
A
A
x
D
A
y
D
1
1
1
2
)
(
j
k
4
4
3
3
2
2
1
1
x
b
x
b
x
b
x
b
y
M(x
j
)
)
(
j
x
x
M
j
j
x
D(x
j
)
R
13
R
24
A
j
A
jj
A
13
A
24
M(x
1
)=
M(x
2
)=
M(x
3
)=
M(x
4
)=
Табл. №2. Сводная таблица для вычислений M(y) и D(y).
)
)
(
)
(
(
2
1
)
(
2
1
4
44
3
33
2
22
1
11
24
24
13
13
4
2
3
1
x
D
A
x
D
A
x
D
A
x
D
A
R
A
R
A
x
x
x
x
)
( y
M
4
2
3
1
24
4
2
13
3
1
4
2
4
3
2
3
2
2
2
1
2
1
)
(
)
(
)
(
)
(
)
(
x
x
x
x
R
A
A
R
A
A
x
D
A
x
D
A
x
D
A
x
D
A
y
D
Получить следующие величины:
-
Вычислим функцию чувствительности A
j
-
Вычислить математическое ожидание M(y) и дисперсию D(y) выходных параметров
Задание №2
Анализ надежности системы с восстановлением элементов после их отказа
Анализ проведем для двух случаев, когда система состоит из двух и трех элементов.
1. Система состоит из двух элементов: технологического агрегата (ТА) и обслуживающего
этот агрегат промышленного робота (ПР) ( Рис. 1 ).
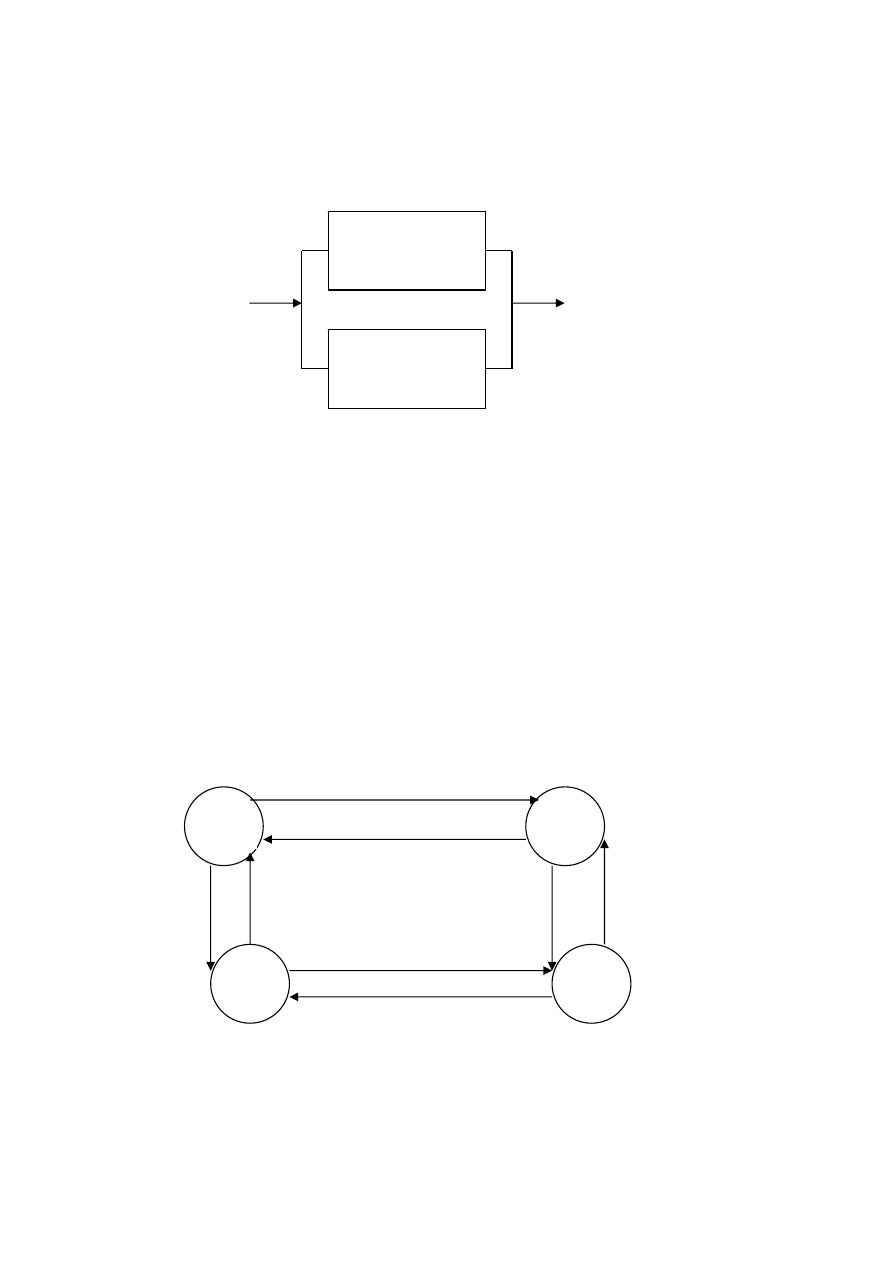
Рис. 1. Система из двух элементов
Интенсивности отказов и восстановлений каждого элемента независимы и известны.
Отказ любого элемента приводит к отказу всей системы.
Считаем, что:
Интенсивность отказов ТА-
1
,
ПР-
2
Интенсивность восстановлений ТА-
1
,
ПР-
2
Общее число возможных состояний -
4
2
2
.
Составим граф возможных состояния системы ( Рис.2.).
Рис. 2. Граф возможных состояния системы
11
S
10
S
01
S
00
S
)
(
11
t
P
)
(
10
t
P
)
(
00
t
P
)
(
01
t
P
2
1
2
2
2
1
1
1
ТА
ПР

Обозначения:
S – состояния системы, P(t)- вероятность нахождения в этом состоянии.
S
11
– работают ТА и ПР;
S
10
– работает ТА, ПР -отказал в работе;.
S
01
– ТА отказал в работе, ПР- работает ;
S
00
– отказали оба элемента
Первая цифра в индексе соответствует состоянию ТА, вторая –ПР
Уравнения состояния системы:
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
00
2
00
1
10
1
01
2
00
01
1
00
2
11
1
01
2
01
10
2
00
1
11
2
10
1
10
01
1
10
2
11
2
11
1
11
t
P
t
P
t
P
t
P
dt
t
dP
t
P
t
P
t
P
t
P
dt
t
dP
t
P
t
P
t
P
t
P
dt
t
dP
t
P
t
P
t
P
t
P
dt
t
dP
1
)
(
00
01
10
11
t
P
t
P
t
P
t
P
Для установившегося режима системы левые части уравнений равны нулю и дифференциальные
уравнения преобразуются в систему алгебраических уравнений.
2. Система состоит из трех элементов и представляет собой робототехнический комплекс ( РТК
) состоящий из: сборочного технологического оборудования ( ТО ) , загрузочного и разгрузочного
промышленных роботов ( ПР1 и ПР2 ). После отказа любого элемента необходимо восстановить
его работоспособность и, следовательно, работоспособность всей системы. Для оценки
надежности такой системы необходимо:
-задать интенсивности потока отказов элементов
-составить граф состояний системы
-по графу составить систему уравнений состояния системы и решить их.
Задача
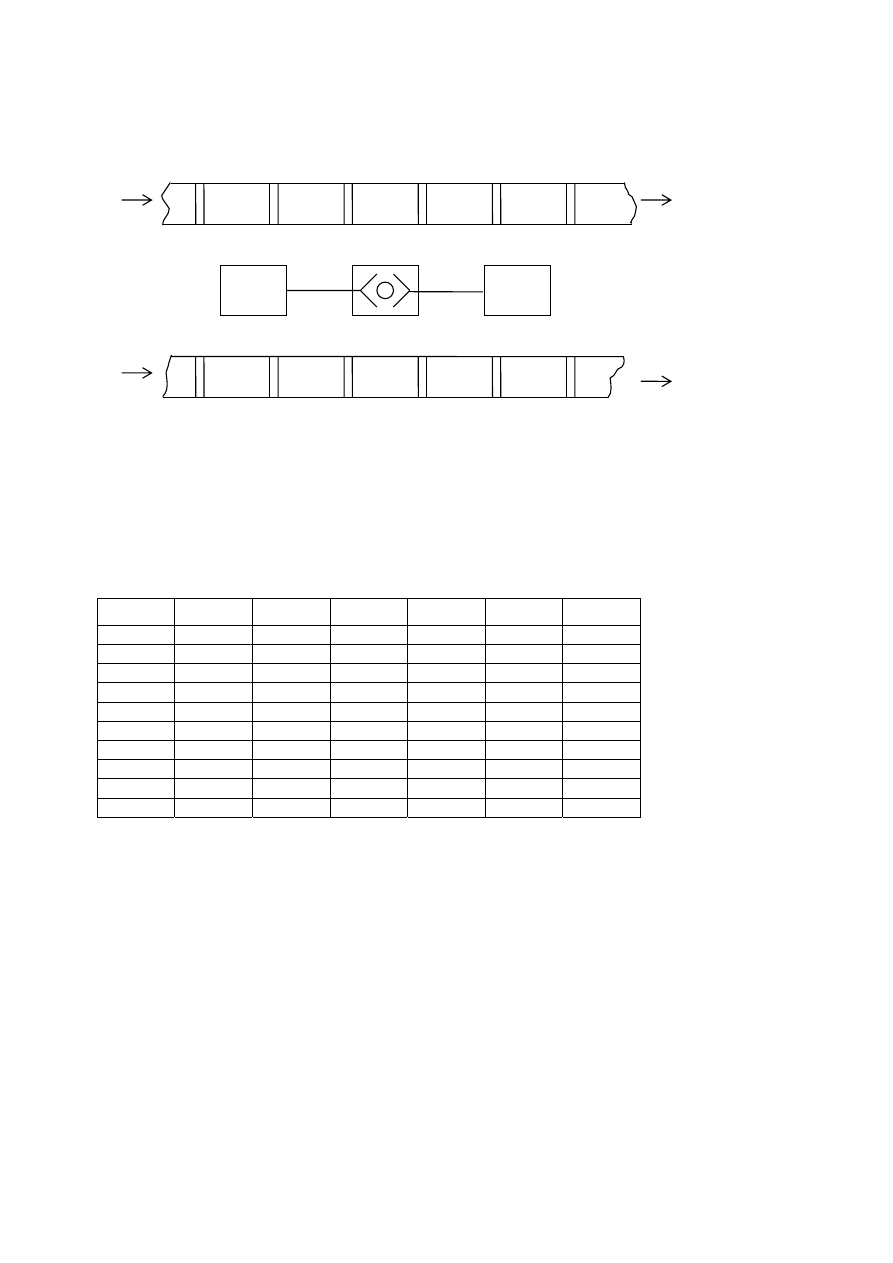
Рис. 3. Схема РТК
РТК состоит из трёх элементов ( Рис. 3.):
загрузочного робота ПР1 (интенсивность отказа –
1
; интенсивность восстановления –
1
)
Сборочного технологического оборудования ТО (интенсивность отказа –
2
; интенсивность
восстановления –
2
)
разгрузочного робота ПР2 (интенсивность отказа –
3
; интенсивность восстановления –
3
)
Варианты
Вариант
1
1
2
2
3
3
1
1/10
1
1/100
1
1/15
1
2
1/20
2
1/200
2
1/30
1
3
1/30
3
1/300
3
1/40
1
4
1/40
4
1/400
4
1/70
1
5
1/10
1
1/500
5
1/10
1
6
1/20
2
1/600
6
1/25
1
7
1/40
3
1/700
7
1/55
1
8
1/30
4
1/800
8
1/75
1
9
1/20
1
1/900
9
1/5
1
10
1/10
2
1/150
1
1/35
1
Найти
Вероятность того, что все элементы находятся в рабочем состоянии;
вероятность того, что все элементы отказали;
остальные вероятности.
вероятность отказа системы
Система имеет 2
3
возможных состояний: 000, 001, 010, 011, 100, 101, 110, 111. Где 1 – элемент в
работоспособном состоянии, 0 – отказ. Позиционно первая цифра соответствует ПР1, вторая – ТО,
ПР 1
ПР 2
ТО
детали
изделия

третья – ПР2. Система неработоспособна при отказе любого элемента. Отказы независимы (отказ
одного элемента не влечёт за собой отказ другого).
Граф состояний будет иметь вид …..
Запишем уравнения Колмогорова:…….
В стационарном режиме после переходного периода элементарные вероятности состояний не
меняются и производные по вероятности стремятся к нулю, следовательно, в стационарном
режиме система дифференциальных уравнений превращается в систему алгебраических
уравнений, которую можно решить (например, в МATHLAB).
…..
Вывод:
В результате получили следующие значения.
Вероятность того, что все элементы находятся в рабочем состоянии
111
P
;
вероятность того, что все элементы отказали
000
P
.
Остальные вероятности.
101
100
011
010
001
P
P
P
P
P
110
P
.
В итоге получаем вероятность отказа системы
отк
P
Задача №3
Автоматизированные поточные линии.
Теоритическая часть
АПЛ состоят из АТО и автоматизированных транспортных средств.
Под ПЛ понимается производственный участок, на котором ТП организован на основе принципов
пропорциональной производительности всех элементов, параллельности( при параллельной
структуре ТП ), ритмичности и непрерывности (отсутствие перерывов между ТО ).
Классификация ПЛ.
В зависимости от номенклатуры изделий ПЛ подразделяются на ОНПЛ и МНПЛ.
По степени синхронизации ТО на непрерывные и прерывные.
По степени автоматизации на автоматизированные и неавтоматизированные.
Расчет организационно-производственных параметров ОНПЛ.
При проектировании ОНПЛ рассчитываются следующие ОПП:
1. ритм ОНПЛ
2. число рабочих мест на каждой ТО,
3. число мест обработки на линии,
4. коэффициент загрузки ОНПЛ,
5. необходимые заделы на поточной линии.
6 .выбор схемы расположения оборудования
Расчеты производятся по формулам: