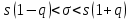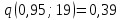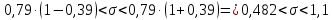Файл: Решение Выполним замену Выполним замену переменной.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 34
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Выборочное среднее:
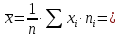
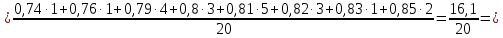
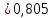
Выборочная дисперсия:
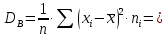
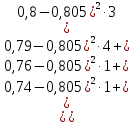
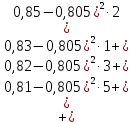
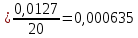
Исправленная выборочная дисперсия:
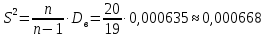
Исправленное СКО:
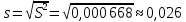
Доверительный интервал для неизвестного математического ожидания:
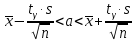
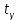 найдем по таблице распределения Стьюдента при
найдем по таблице распределения Стьюдента при 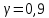 и
и 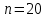
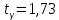
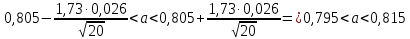
Доверительный интервал для неизвестного СКО:
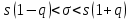
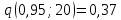
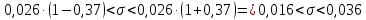
Задание №6
Результаты независимых наблюдений над случайной величиной
 , характеризующей отклонение длины детали, от требуемой по техническим условиям, представлены в виде простого статистического ряда. Необходимо построить статистический (вариационный) ряд и гистограмму, найти оценки для математического ожидания и дисперсии, построить соответствующие доверительные интервалы для данного значения
, характеризующей отклонение длины детали, от требуемой по техническим условиям, представлены в виде простого статистического ряда. Необходимо построить статистический (вариационный) ряд и гистограмму, найти оценки для математического ожидания и дисперсии, построить соответствующие доверительные интервалы для данного значения 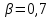 . Подобрать теоретическую функцию распределения.
. Подобрать теоретическую функцию распределения.| 19,5 | 19,72 | 20,1 | 20,21 | 20,44 |
| 19,8 | 20,05 | 20,6 | 22,3 | 22,1 |
| 21,2 | 21,35 | 21,58 | 21,62 | 20,71 |
| 20,89 | 21,1 | 21,15 | 21,8 | |
Решение:
Объем выборки
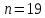
Упорядочим данные в выборке по возрастанию:
| 19,5 | 19,72 | 19,8 | 20,05 | 20,1 |
| 20,21 | 20,44 | 20,6 | 20,71 | 20,89 |
| 21,1 | 21,15 | 21,2 | 21,35 | 21,58 |
| 21,62 | 21,8 | 22,1 | 22,3 | |
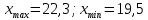
Размах выборки:
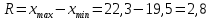
Разобьем выборку на 5 интервалов
Длина интервала:
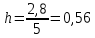
Вычислим частоты
 попадания в интервалы, относительные частоты
попадания в интервалы, относительные частоты 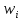 , и плотности относительных частот
, и плотности относительных частот 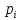 . Вычислим середины интервалов
. Вычислим середины интервалов 
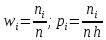
| Интервал | 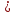 | 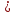 | 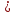 |  | 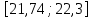 |
 | 19,78 | 20,34 | 20,9 | 21,46 | 22,02 |
 | 4 | 4 | 4 | 4 | 3 |
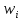 | 0,211 | 0,211 | 0,211 | 0,211 | 0,158 |
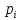 | 0,376 | 0,376 | 0,376 | 0,376 | 0,282 |
Построим гистограмму относительных частот – столбчатую диаграмму, основаниями которой служат частичные интервалы, а высотами плотности относительных частот:
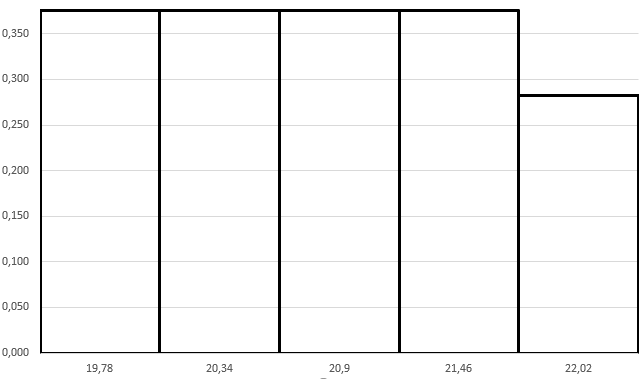
Выборочное среднее:
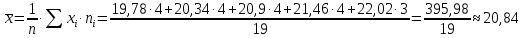
Выборочная дисперсия:
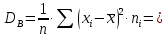
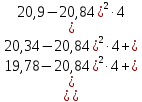
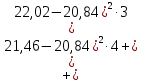
Исправленная выборочная дисперсия:
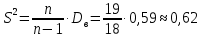
Исправленное СКО:
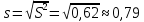
Доверительный интервал для неизвестного математического ожидания:
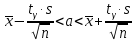
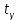 найдем по таблице распределения Стьюдента при
найдем по таблице распределения Стьюдента при 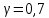 и
и 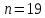
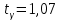
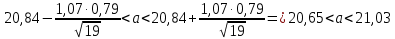
Доверительный интервал для неизвестного СКО: