Файл: Двойные углы 3 Sin2X Рассмотрим выражение sin2x представим его аргумент в виде 2xxx и воспользуемся известной формулой синуса суммы аргументов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 152
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– полуоси эллипса, причём 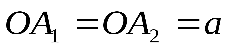 – большие полуоси;
– большие полуоси; 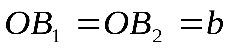 – малые полуоси.
– малые полуоси.
4. Когда фокусы эллипса расположены на оси , имеем, что
, имеем, что 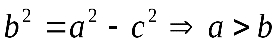 . Когда фокусы располагаются на оси
. Когда фокусы располагаются на оси  ,
, 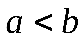 , тогда
, тогда 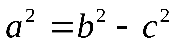 .
.
Определение 9.3. Фокальными радиусами точки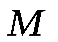 , принадлежащей эллипсу, называются отрезки, соединяющие эту точку с фокусами и . Для каждой точки эллипса существует два фокальных радиуса. Обозначаются:
, принадлежащей эллипсу, называются отрезки, соединяющие эту точку с фокусами и . Для каждой точки эллипса существует два фокальных радиуса. Обозначаются: 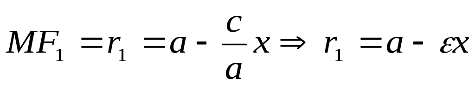 ,
,
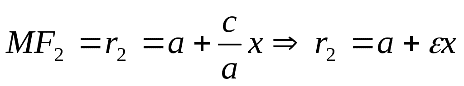 .
.
ведем прямоугольную систему координат. Пусть фокусы гиперболы
лежат на оси Ох, причем - середина отрезка , тогда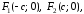 т. е.
т. е.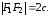 Пусть
Пусть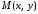 – произвольная точка гиперболы. Величины
– произвольная точка гиперболы. Величины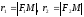 –фокальные радиусыточки М гиперболы.(чертеж 17.)
–фокальные радиусыточки М гиперболы.(чертеж 17.)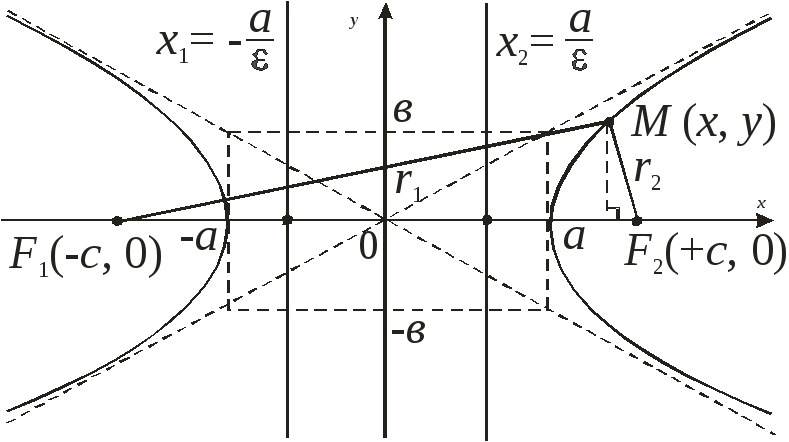
По определению гиперболы: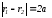 , отсюда
, отсюда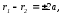 где
где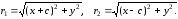
Следовательно, уравнение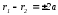 имеет вид:
имеет вид: 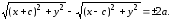 (7)
(7)
Умножим равенство (7) на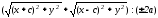 , получим:
, получим: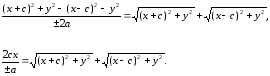
Сложим уравнения (7) и (8), получим: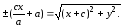 (9)
(9)
Возведем (9) в квадрат: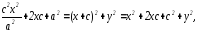 следовательно, имеем:
следовательно, имеем: 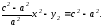
Пусть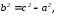 так как
так как 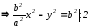
, отсюда имеем уравнение: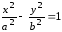 (10) где (10) каноническое уравнение гиперболы с центром в начале координат.
(10) где (10) каноническое уравнение гиперболы с центром в начале координат.
Соответственно, уравнение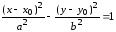 где каноническое уравнение гиперболы с центром в точке
где каноническое уравнение гиперболы с центром в точке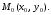
Числа a и b соответственно действительная и мнимая полуоси гиперболы
4)Исследование свойств гиперболы по ее уравнению 1) Пересечение гиперболы с осями координат: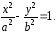
Очевидно, что гипербола состоит из двух ветвей: правой и левой, простирающихся в бесконечность.
В уравнении (12) положим, что y=0, получим: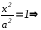
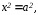 отсюда . Следовательно, точки
отсюда . Следовательно, точки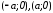 являются точками пересечения гиперболы с осью (чертеж 18.).
являются точками пересечения гиперболы с осью (чертеж 18.).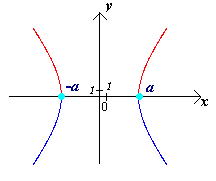
Положим, что в уравнении (12) х=0, и получим: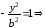
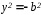 , следовательно, уравнение гиперболы не пересекает ось .
, следовательно, уравнение гиперболы не пересекает ось .
ЗАМЕЧАНИЕ: Если мнимая ось гиперболы имеет длину 2a и направлена по оси (OX), а действительная ось длиной 2b совпадает с осью (OY), то уравнение гиперболы имеет вид: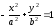 . [1.С.107-108]
. [1.С.107-108]
Определение 3.2. Гиперболы, заданные уравнениями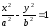 и
и 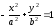
, называются сопряженными гиперболами.
Определение 3.3. Если a=b, гипербола называется равносторонней.
2) Симметрии гиперболы относительно координатных осей и:
Пусть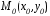 принадлежит гиперболе, то есть
принадлежит гиперболе, то есть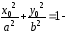 верное равенство. Точка
верное равенство. Точка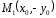 симметрична точке относительно оси ОХ:
симметрична точке относительно оси ОХ:
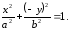
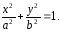 - верное равенство. Следовательно, принадлежит гиперболе, следовательно, гипербола симметрична относительно ОХ.
- верное равенство. Следовательно, принадлежит гиперболе, следовательно, гипербола симметрична относительно ОХ.
Точка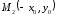 симметрична точке относительно оси ОУ, следовательно, гипербола симметрична относительно оси ОУ.
симметрична точке относительно оси ОУ, следовательно, гипербола симметрична относительно оси ОУ.
Точка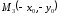 симметрична точке относительно О (центра), отсюда следует, что гипербола симметрична относительно начала координат. [1.С.108]
симметрична точке относительно О (центра), отсюда следует, что гипербола симметрична относительно начала координат. [1.С.108]
Асимптота: Текущая точка гиперболы при движении по ней в бесконечность неограниченно приближается к некоторой прямой, которая называется асимптотой гиперболы. Асимптотами являются прямые, которые имеют следующие уравнения: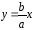 и
и 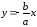 ,
,
Пусть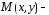 текущая точка гиперболы, ее проекция на ось абсцисс. Прямая пересекает прямую , заданную указанным уравнением в точке . Докажем: что
текущая точка гиперболы, ее проекция на ось абсцисс. Прямая пересекает прямую , заданную указанным уравнением в точке . Докажем: что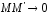 при .
при .
Доказательство: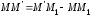 .Расстояние это ордината точки , лежащей на прямой . Она равна
.Расстояние это ордината точки , лежащей на прямой . Она равна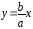 . Расстояние э
. Расстояние э
то ордината точки гиперболы, которую находим из её канонического уравнения: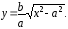 Тогда
Тогда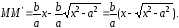
Умножим и разделим равенство (13) на ( ),следовательно, получим: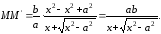
При знаменатель дроби неограниченно увеличивается, следовательно, дробь стремится к нулю.
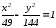 - уравнение гиперболы,
- уравнение гиперболы,
в которой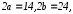 а
а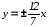
4. Когда фокусы эллипса расположены на оси
Определение 9.3. Фокальными радиусами точки
Вопрос 15
ведем прямоугольную систему координат. Пусть фокусы гиперболы
лежат на оси Ох, причем - середина отрезка , тогда

По определению гиперболы:
Следовательно, уравнение
Умножим равенство (7) на
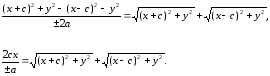
Сложим уравнения (7) и (8), получим:
Возведем (9) в квадрат:
Пусть
, отсюда имеем уравнение:
Соответственно, уравнение
Числа a и b соответственно действительная и мнимая полуоси гиперболы
4)Исследование свойств гиперболы по ее уравнению 1) Пересечение гиперболы с осями координат:
Очевидно, что гипербола состоит из двух ветвей: правой и левой, простирающихся в бесконечность.
В уравнении (12) положим, что y=0, получим:

Положим, что в уравнении (12) х=0, и получим:
ЗАМЕЧАНИЕ: Если мнимая ось гиперболы имеет длину 2a и направлена по оси (OX), а действительная ось длиной 2b совпадает с осью (OY), то уравнение гиперболы имеет вид:
Определение 3.2. Гиперболы, заданные уравнениями
, называются сопряженными гиперболами.
Определение 3.3. Если a=b, гипербола называется равносторонней.
2) Симметрии гиперболы относительно координатных осей и:
Пусть
Точка
Точка
Вопрос 16
Асимптота: Текущая точка гиперболы при движении по ней в бесконечность неограниченно приближается к некоторой прямой, которая называется асимптотой гиперболы. Асимптотами являются прямые, которые имеют следующие уравнения:
Пусть
Доказательство:
то ордината точки гиперболы, которую находим из её канонического уравнения:
Умножим и разделим равенство (13) на ( ),следовательно, получим:
При знаменатель дроби неограниченно увеличивается, следовательно, дробь стремится к нулю.
в которой