5.3.2.5. Построим графики зависимостей , , , и сравним их с аналогичными зависимостями, полученными в п. 5.3.1.5.





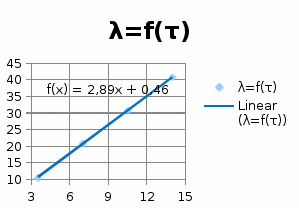
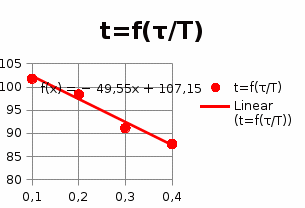
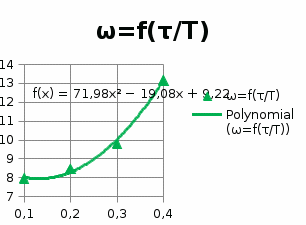
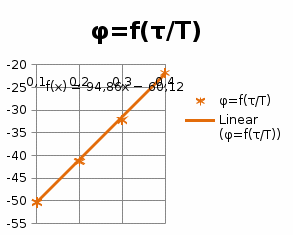
5.3.2.6. Оценим влияние постоянной времени форсирующего звена на характеристики инерционного форсирующего звена.

Из графиков видно, что линейная функция, т.е., с увеличением линейно уменьшается , , в пределах ошибки измерения, не является линейной функцией, т.е., с увеличением уменьшается не линейно, – линейная функция, т.е., с увеличением линейно увеличивается . Зависимость является линейной, т.е., с увеличением

---

увеличивается .

5.3.3 Исследование звеньев второго порядка

5.3.3.1. Собираем схему модели звена второго порядка в соответствии с рис. 5.11. Приняв кОм, мкФ, и выбрав значения постоянной времени и коэффициента передачи из табл. 5.2 согласно индивидуальному варианту, рассчитаем значения остальных параметров модели по формулам:

, , .






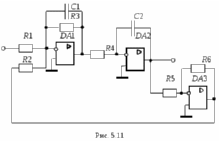
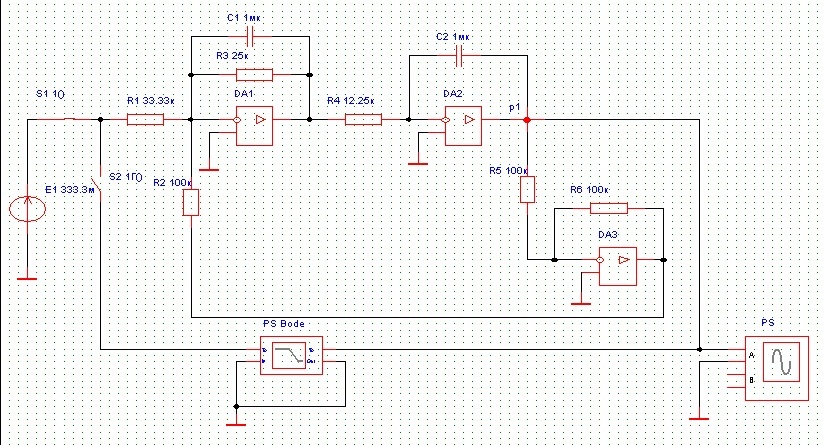
5.3.3.2. Установим напряжение питания модели, равное , снять переходную характеристику и определим время переходного процесса , фиксируя при этом осциллографом максимальное значение выходного напряжения.

5.3.3.3. Рассчитаем перерегулирование

,

Где В. При правильном расчете параметров электронной модели колебательного звена перерегулирование не должно превышать 5 %.



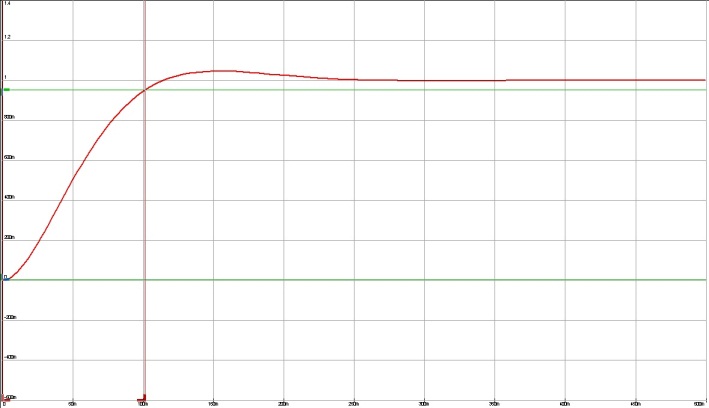
5.3.3.4. Получим экспериментальные ЛАЧХ и ЛФЧХ, замерим частоту среза

---

, значение фазы на частоте среза и определить запас устойчивости по фазе .



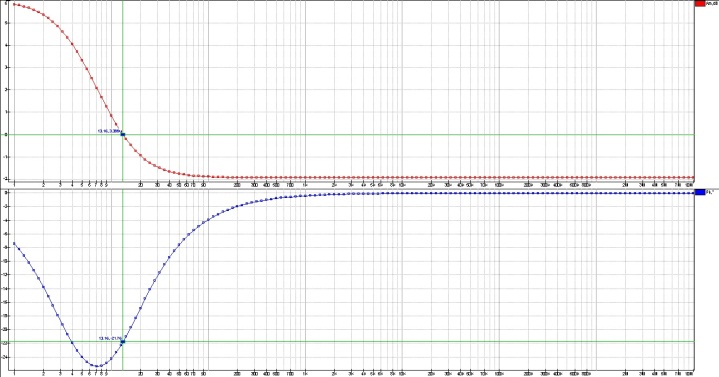
5.3.3.5. Установим значения , , , а также , , и повторим выполнение пп. 5.3.3.2— 5.3.3.4.

Результаты измерения в таблице:

ξ	Umax	U	σ	t	ω	φ	Δφ
0,1	1,7306	1	73,06	56,1	9,129	-172,4	7,6
0,3	1,3726	1	37,26	65,5	8,669	-156,4	23,6
0,5	1,165	1	16,5	78,75	8,233	-141,3	38,7
0,7	1,0476	1	4,76	100,95	7,819	-129	51
1	1	1	0	165,4	6,661	-110,8	69,2
2	1	1	0	299,9	3,422	-81,76	98,24
3	1	1	0	316,95	2,095	-74,05	105,95
4	1	1	0	330,2	1,704	-73,56	106,44

---

5.3.3.6. Построим графики зависимостей , , и .





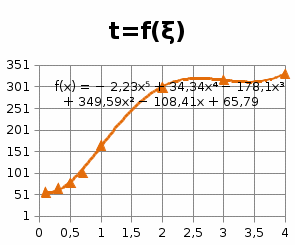
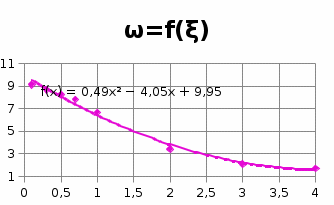
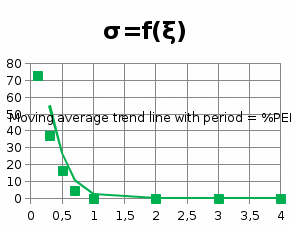
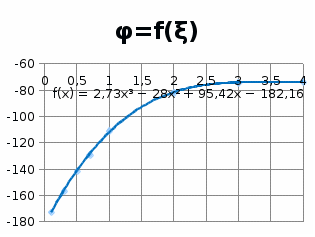
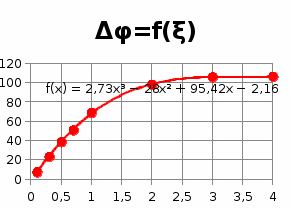
5.3.3.7. Оценить влияние коэффициента демпфирования на характеристики звеньев второго порядка.

Анализ результатов работы.

Влияние постоянной времени на апериодическое звено:

- при увеличении постоянной времени увеличивается время переходного процесса, уменьшается частота среза, сдвиг фазы не меняется, т.е. запас устойчивости по фазе не зависит от постоянной времени.

Влияние форсирующего звена на инерционное:

- увеличивается время переходного процесса, полоса пропускания частот уменьшается снижается запас устойчивости по фазе.

Влияние коэффициента демпфирования на колебательное звено:

- коэффициент демпфирования колебательного звена увеличивает полосу пропускания частот, время переходного процесса увеличивается, перерегулирование увеличивается, запас устойчивости по фазе снижается.

5.3.4 Контрольные вопросы

1. 
   Как количественно величина постоянной времени связана с временем переходного процесса в инерционном звене?
   

Исходя из экспериментальных данных (график, таблица), можно увидеть зависимость , следовательно, постоянная времени T инерционного звена пропорционально увеличивается с увеличением времени переходного процесса .

2. 
   Как изменятся характеристики инерционного форсирующего звена при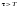 и его реализация на электронной модели?
   

---

Характеристики изменятся следующим образом:

в начальный момент будет скачок напряжения, время переходного процесса уменьшится.

АЧХ и ФЧХ будут иметь следующий вид:

Исчезнет частота среза ωср (т.е. звено будет иметь усилительные свойства на всех частотах). Значение фазы φ ср изменяется от близкого к нулю, затем с увеличением АЧХ принимает отрицательное значение, а потом снова близкое к нулю.

3. 
   В каком случае колебательное звено становится консервативным и как при этом изменятся его характеристики?
   

Колебательное звено становится консервативным, когда коэффициент демпфирования равен нулю, колебания переходного процесса становятся незатухающими, амплитуда на сопрягающей частоте становится бесконечной, фаза скачком из 0 становится равной –π.

4. 
   Как нужно изменить схему, приведенную на рис. 5.11, чтобы получить электронную модель консервативного звена?
   

Исключив сопротивление R3-обратной связи первого каскада, получим из колебательного звена консервативное.

5. 
   Чему равен запас устойчивости по амплитуде в звеньях второго порядка?
   

Запас устойчивости по амплитуде в звеньях второго порядка для всех ξ показан на таблице:

ξ	G(ωπ)
0,1	85,06
0,3	104,4
0,5	113,5
0,7	118,9
1	125,4
2	137,5
3	144,7
4	149,7

6. 
   Чем объяснить наличие точки перегиба на переходной характеристике апериодического звена второго порядка?
   

Апериодическое звено второго порядка состоит из двух последовательно соединенных апериодических звеньев первого порядка, в связи с этим при суммировании двух экспоненциальных составляющих происходит перегиб.

---

Смотрите также файлы

• Когда принял заказ, и не записал его Действующее лицо девушка официант.docx

• Выявление ошибок системных компонентов.docx

• Курсовая работа по дисциплине ботаника происхождение и основные направления в эволюции водорослей.docx

• Проведения занятий.rtf

• Введение 3 глава теоретическая часть. Теоретические вопросы анализа финансового состояния. 5.docx