Задача №1. Циклы поршневых двигателей внутреннего
сгорания.

Для идеального цикла поршневого двигателя внутреннего сгорания с подводом теплоты при постоянном давлении или постоянном объеме определить параметры рабочего тела в характерных точках цикла, полную работу, количество подведенной и отведенной теплоты, термических КПД цикла. Изобразить цикл
двигателя в p-v и T-s диаграммах. Константы рабочего тела (продуктов сгорания) принять по воздуху. Удельную теплоемкость воздуха принять независящей от температуры и равной с_р = 1,04 кДж/(кг·К), k = с_р/с_v = 1,4.

Начальное давление p₁ принять равным атмосферному, начальную температуру t₁ – равной температуре окружающего воздуха.

Данные для решения задачи выбрать из табл. 1.

Таблица 1

Данные для расчета цикла ДВС

№ варианта	ε	λ	ρ	t1, °С	Атмосферное давление, мм.рт.ст
1	11	-	2,2	5	750

Решение:

Определим c_v = c_p/k = 1,04/1,4 =0,743 кДж/(кг·К), R = c_p – c_v = 1,04 – 0,743 = 0,297 кДж/(кг·К).

1) Определим параметры в характерных точках цикла.

а) точка 1, зная P₁ = 750 мм.рт.ст, t₁ = 5 °С, зная что 1 мм.рт.ст. = 133,3 Па P₁ = 750·133,32 = 99975 Па = 0,99975 бар, T₁ = 5 + 273 = 288 К

определим значение v₁

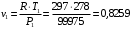м³/кг

б) точка 2, так как процесс 1-2 адиабатный, k = 1,4

v₂ = v₁/ ε = 0,8259/11 = 0,0751 м³/кг

P₂ = P₁· ε^k = 0,99975·11^1,4 = 28,697 бар

T₂ = T₁· ε^{k – 1} = 278·11^{1,4 – 1} = 725,4 К = 452,4 ⁰С

в) точка 4, процесс 3-4 изобарный

P₃ = P₂ = 22,697 бар

v₃ = v₂· ρ = 0,0751·2,2 = 0,1652 м³/кг

T₄ = ρ ·λ ·T₁· ε^{k -1} = 2,2·1·278·11^{1,4 – 1} = 1596,0 К = 1323,0 ⁰С

г) точка, процесс 3-4 адиабатный, процесс 4-1 изохорный

v₄ = v₁ = 0,8259 м³/кг

P₄ = ρ^k ·λ ·P₁ = 2,2^1,4·1·0,99975 = 3,015 бар

---

T₄ = ρ^{k - 1} ·λ ·T₁ = 2,2^{1,4 - 1}·1·278 = 838,4 К = 565,4 ⁰С

Полученные результаты сведем в таблицу

Точка	1	2	3	4
P, бар	0,99975	28,697	28,697	3,015
v, м3/кг	0,8259	0,0751	0,1652	0,8259
T, К	278,0	725,4	1596,0	838,4
t, 0C	5,0	452,4	1323,0	565,4

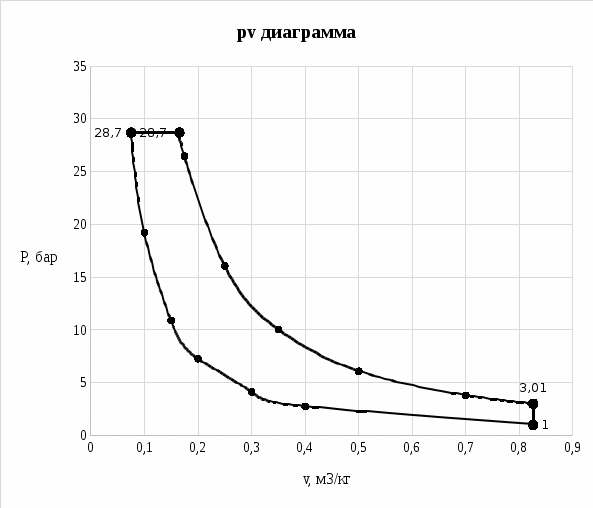
2) Полезная работа цикла

l₀ = =

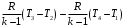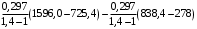= = 488,84 кДж/кг

3) Количество подведенной, отведенной и полезной теплоты

количество подведенной теплоты

q₁ = c_p·(T₄ – T₃) = 1,04·(1596,0 – 725,4) = 905,35 кДж/кг

количество отведенной теплоты

q₂ = c_v·(T₄ – T₁) = 0,743·(838,4 – 278) = 416,36 кДж/кг

Полезная работа цикла

l = l₀ = q₁ – q₂ = 905,35 – 416,36 = 488,99 кДж/кг

4) термический КПД







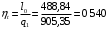
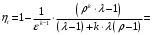
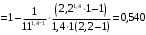
Вопросы

1) Как влияет степень сжатия на термический КПД цикла?

При повышении степени сжатия кпд цикла увеличивается. Это видно из формулы цикла с подводом теплоты при постоянном объеме



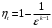
2) КПД какого цикла (при р = const или v = const) больше при одинаковых степенях сжатия? Ответы иллюстрировать изображением циклов в p-v и T-s диаграммах.

---

КПД цикла v = const больше при одинаковых степенях сжатия.



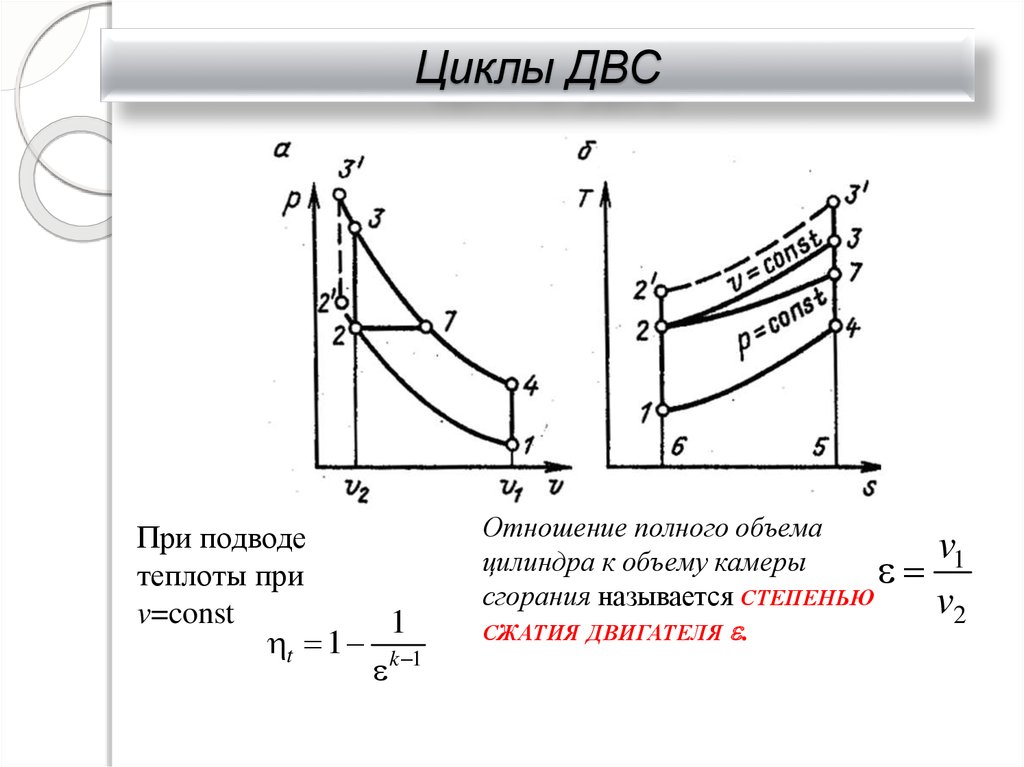
3) Как изменится КПД ДВС с уменьшением показателя адиабаты k?

При уменьшении показателя адиабаты k, для уравнения кпд величина знаменателя уменьшается, соответственно уменьшается и значение кпд.




Задача №2 Второй закон термодинамики.
Изменение энтропии в равновесных процессах.

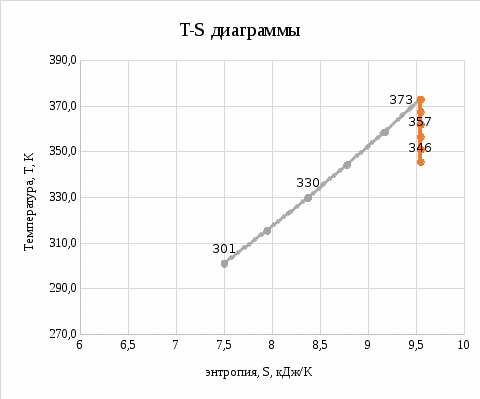
Газ массой М имеет начальные параметры - давление р₁, и температуру t₁. После политропного изменения состояния объем газа стал V₂ а давление р₂^пол. Определите характер процесса (расширение или сжатие газа), показатель политропы n, конечную температуру t₂, теплоемкость политропного процесса с, работу и теплоту в процессе, а также изменение внутренней энергии и энтропии газа. Определите эти же величины и конечное давление р₂, если изменение состояния газа до того же объема V₂ происходит: а) по изотерме и б) по адиабате. Составьте сводную таблицу результатов расчета, изобразите совмещено все процессы в pv- и Ts- диаграммах.

Данные для решения задачи выберите из таблицы 2.

Предпоследняя цифра шифра	Газ	t1, °С	p1, МПа3	Последняя цифра шифра	M, кг	p2пол, МПа	V2, м3
0	NH3	100	0,5	0	5,0	0,25	3,3
1	O2	150	0,55	1	10,0	0,32	4,6

Решение

Молярная масса NH₃ μ_NH3= 17 кг/кмоль.

---

Газовая постоянная NH₃:

R_NH3 = μR/ μ_NH3 = 8314/17 = 489,1 Дж/кг К = 0,4891 кДж/кг·К

Изохорная теплоемкость NH₃, k = 1,33 – показатель адиабаты для многоатомного газа

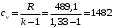Дж/кг К = 1,482 кДж/кг·К

Изобарная теплоемкость NH₃, k = 1,33 – показатель адиабаты для многоатомного газа

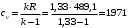Дж/кг К = 1,971 кДж/кг·К

Объем V₁ аммиака найдем из уравнения состояния



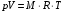
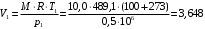кг

Так V₁ < V₂, то происходит расширения газа

Показатель политропы определим из соотношения





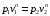
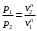
Прологарифмируем выражение



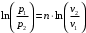
откуда показатель политропы



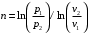
Отсюда



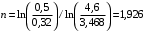
Температура в конце процесса

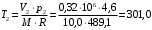К = 28,0 ⁰С

Количество теплоты

Q = c·M·(T₂ – T₁) = 10·0,954·(28,0 – 100) = -686,7 кДж

Теплоемкость политропного процесса



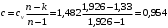
Работа в политропном процессе

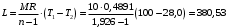кДж/кг

Работа

L = R/(n – 1)·M·(T₁ – T₂) = 0,4891/(1,926 – 1)·10·(28.0 – 100) = 380 кДж

Изменение внутренней энергии

ΔU = c_v·(T₂ – T₁) = 10·1,482·(28.0 – 100) = -1067,24 кДж

Изменение энтропии



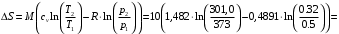
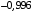= кДж/К

а) изотермический процесс

Параметры конечного состояния газа

p₂ = p₁V₁/V₂ = 0,5·3,468/4,6 = 0,3966 МПа

T₂ = T₁ = (100 + 273) = 373 К = 100 °С

Количество теплоты

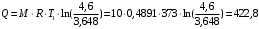кДж

Работа

L = Q = 422,8 кДж

Изменение внутренней энергии

ΔU = c_v

---

·(T₂ – T₁) = 1,482·(373– 373) = 0

Изменение энтропии

1,336 кДж

б) адиабатный процесс

Параметры конечного состояния газа

p₂ = p₁/ε^k = 0,5/1,261^1,33 = 0,367 МПа

T₂ = T₁/ε^k-1 = (100 + 273)/1.261^1,33-1 = 345,6 К = 72,5 °С

Количество теплоты

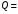0 кДж

Работа

L = R/(k – 1)·M·(T₁ – T₂) = 0,4891/(1,33 – 1)·10·(100 – 72,5) = 407.0 кДж

Изменение внутренней энергии

ΔU = c_v·(T₂ – T₁) = 10·1,482·(72.5 –100) = -407.0 кДж

Изменение энтропии

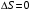кДж



Задача №1 Термодинамические процессы в идеальных

Газовая смесь массой M₁, заданная по объемному составу, нагревается
при постоянном объеме V₁ от температуры t₁ до температур t₂, охлаждается при постоянном давлении до начальной температуры t₁.

Определите конечные давления и объем смеси, величину работы и теплоты, участвующих в процессах, изменение внутренней энергии и энтропии смеси в каждом процессе. Расчет иллюстрировать изображением процессов в pv- и Ts- координатах.

Данные для решения задачи выбрать из таблицы 1.

Предпоследняя цифра шифра	M, кг	V1, м3	t1, °С	t2, °С	Последняя цифра шифра	Состав газовой смеси.%
						N2	O2	CO2	Н2O	СО	Н2
0	25	20	80	550	1	79	21	-	-	-	-

---

Смотрите также файлы

• Методические рекомендации для обучающихся по составлению и выполнению отчета о прохождении всех видов практики специальность 40. 02. 01. Право и организация социального обеспечения.doc

• Сущность и содержание проблемы утечки умов 4 Основные причины интеллектуальной миграции 6.doc

• Эпимизий (покрывает мышцу снаружи)Перимизий (окружает пучки волокон)Эндомизий.pdf

• Занятие 1 Тема 1 деньги сущность, функции, виды и обращение задание 1.doc

• Рецензия на книгу " в кварталах дальних и печальных Избранная лирика. Роттердамский дневник".docx