Файл: Лабораторная работа 10 Решение задач по основам количественной теории информации Фамилия Имя Отчество.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 68
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,
СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ
Дисциплина: Теория информации, знания, данные
ЛАБОРАТОРНАЯ РАБОТА 10
«Решение задач по основам количественной
теории информации»
Фамилия:
Имя:
Отчество
Группа №: ИБ-16с
№ Зач:
Проверил:______________
Санкт-Петербург
2023
Таблица 1
| Последняя цифра шифра | 1 |
| p1 | 0,3 |
| p2 | 0,3 |
| p3 | 0,3 |
| p4 | 0,1 |
| M | 6 |
| N | 64 |
| t | 1 |
Задача 1
Источник сообщений выдает символы из алфавита A = {ai}, i = 1, …, 4 с вероятностями (см. таблицу 1) p1, p2, p3, p4. Найти энтропию и избыточность источника сообщений.
Результаты выполнения работы
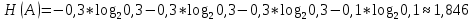 бит
бит По определению избыточности
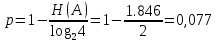
Задача 2
Рассмотрим следующий процесс: мы замеряем некоторую величину ξ, которая является количеством фотонов, которые регистрируются фоточувствительной пластиной. Пусть источник света в единицу времени генерирует N фотонов. Каждый фотон с вероятностью
p1 может рассеяться на частицах среды, находящейся между источником и пластиной и не достичь фоточувствительной пластины. С вероятностью p2 фотон, достигший фоточувствительной пластины, может быть зарегистрирован пластиной.
Какое количество информации содержится в сообщении, что зарегистрировано M фотонов?
Результаты выполнения работы
С помощью формулы Бернулли найдем вероятность того, что за едини-
цу времени будет зарегистрировано 8 фотонов из 256:
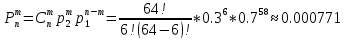
С помощью следующей формулы найдем количество информации и
получим ответ:
I = -log20.000771= 9,60(бит) занимает сообщение о том, что зарегистрировано 8 фотонов из 256.
Задача 3
Первичный алфавит состоит из трех знаков с вероятностями p1, p2,p. При этом p1 и p2 заданы в табл.1 и p1+p2+p=1. Для передачи по каналу без помех используется равномерный двоичный код. Средняя длительность передачи одного элемента сообщения в канале τ=10-6 с. Определить пропускную способность канала и скорость передачи информации. Можно ли приблизить скорость передачи к пропускной способности данной системы?
Результаты выполнения работы
Найдем энтропию источника:
H = −0.3 · log2 0.3 − 0.3 · log2 0.3 − 0.4 · log2 0.4 ≈ 1.57 (бит)
Так как код равномерный, получаем
Найдем скорость передачи информации:
J = KV · H = 10000002 · 1.57 = 78000 (бит/с)
Таким образом, реальная скорость передачи информации меньше пропускной способности. Это происходит из-за того, что каждый символ первичного алфавита, занимая два разряда, несет меньше двух бит информации. Если приблизить длину кода К к значению реальной энтропии, можно увеличить скорость передачи информации.
Задача 4
Сколько информационных и проверочных символов содержится в двоичном коде, исправляющем ровно t ошибок при общем числе разрешенных кодовых комбинаций
, равном N (см. таблицу 1).
Результаты выполнения работы
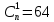
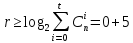
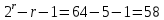
В двоичном коде содержится 58 информационных, 5 проверочных символов.
Выводы по работе
В ходе работы были решены четыре задачи на темы количественной меры информации, энтропии, основ теории передачи информации и помехоустойчивого кодирования сообщений. В процессе решения задач использовались формулы из теории вероятностей (Бернулли) и формулы для нахождения значения энтропии, избыточности источника сообщения, определения количества информации, пропускной способности канала и скорости передачи информации, а также формулы для работы с корректирующими способностями кода и кодом Хемминга.