Файл: Учебное пособие Томск 2001 удк.doc

5. ТЕПЛОПЕРЕДАЧА СО СЛОЖНЫМ ТЕПЛООБМЕНОМ
НА ПОВЕРХНОСТЯХ СТЕНКИ ПРИ СТАЦИОНАРНОМ РЕЖИМЕ. ИНТЕНСИФИКАЦИЯ ТЕПЛОПЕРЕДАЧИ

5.1. Теплопередача через плоскую стенку
со сложным теплообменом

Сложный теплообмен – это одновременная передача теплоты двумя или тремя способами (конвекцией, теплопроводностью, излучением).

Пусть теплота передается от горячей воды с температурой через плоскую стенку толщиной к окружающему спокойному воздуху с температурой (рис. 5.1).

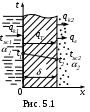Дано:; ; ; коэффициент теплопроводности стенки ; коэффициенты конвективной теплоотдачи ₁, ₂; степень черноты поверхности стенки _с.

Определить: плотность передаваемого теплового потока (q, Вт/м²) и температуры на поверхностях стенки t₁ и t₂.

От воды к поверхности теплота передается путем конвективного теплообмена ( ), через стенку – теплопроводностью ( ), от стенки к воздуху – конвекцией ( ) и излучением ( ).

Таким образом,

, ,	(5.1) (5.2)
,	(5.3)
,	(5.4)
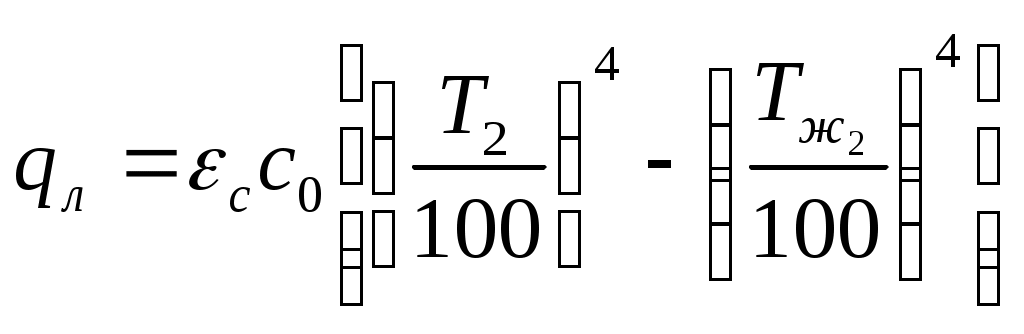.	(5.5)

---

При расчетах теплопередачи со сложным теплообменом на поверхностях суммарную теплоотдачу заменяют эквивалентным тепловым потоком, например конвективным:

.

(5.6)

При подстановке (5.4) в (5.6) получим формулу для расчета эквивалентного коэффициента теплоотдачи

.

(5.7)

Слагаемое учитывает передачу теплоты излучением и называется лучистым коэффициентом теплоотдачи.

В наиболее общем виде формулу для расчета эквивалентного коэффициента теплоотдачи можно записать так:

,

(5.8)

где - абсолютная величина разности температур поверхности и среды.

Таким образом, систему 4^х уравнений (5.2)-(5.5)заменяем системой
3^х уравнений:

,	(5.9)
,	(5.10)
,	(5.11)

совместное решение которых дает расчетную формулу для плотности теплового потока

.

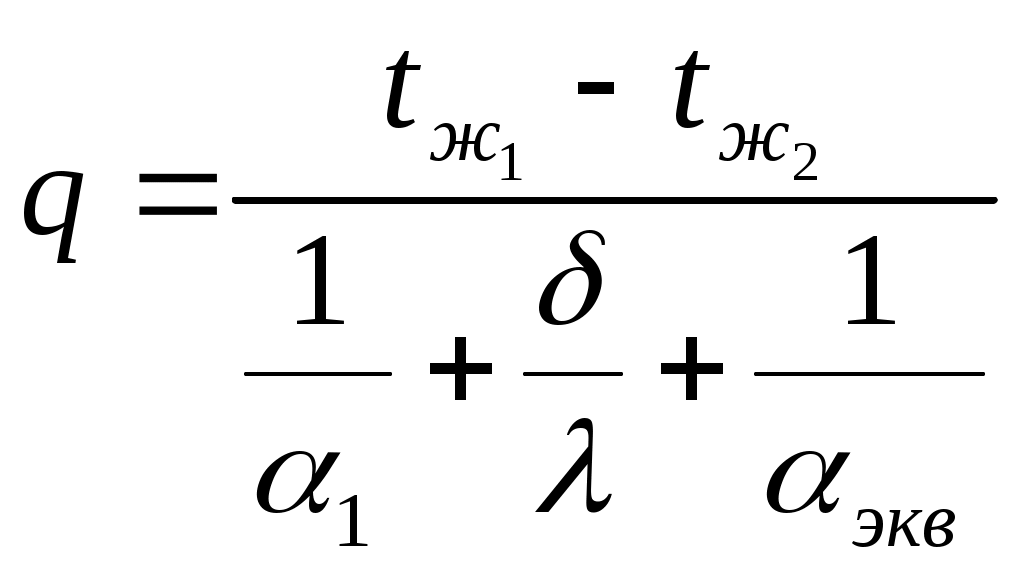(5.12)

Формула (5.12) включает эквивалентный коэффициент теплоотдачи (_экв), который требует знания температуры поверхности со сложным теплообменом (t₂). Так как эта температура неизвестна, то ее задают; по (5.7) с учетом (5.5) рассчитывают _экв, затем по (5.12) рассчитывают q. Правильность задания температуры

---

t₂ проверяют уравнением (5.11). Если температура поверхности t₂,рассчитанная по (5.11), совпадает с заданной – расчет закончен. В противном случае расчет повторяют с температурой t₂, вычисленной по (5.11), до тех пор, пока проверка не подтвердит заданную температуру. Такой метод расчета называется методом последовательных приближений и его не избежать при расчетах теплопередачи со сложным теплообменом на поверхностях.

После того, как найдены qи t₂, рассчитывают температуру t₁ по уравнениям (5.9) или (5.10).

---

5.2. Теплопередача через цилиндрическую стенку
со сложным теплообменом

Рассмотрим передачу теплоты через стенку трубы водяного экономайзера парового котла от дымовых газов со средней температурой , омывающих наружную поверхность трубы, к нагреваемой воде со средней температурой , движущейся по трубе (рис. 5.2).

Д ано: геометрические размеры трубы (d₁, d₂, ), коэффициент теплопроводности материала трубы (λ), температура дымовых газов ( ) и воды ( ), конвективные коэффициенты теплоотдачи (α₁, α₂), степень черноты наружной поверхности трубы (_с).

Определить:передаваемый через стенку трубы тепловой поток (Q, Вт) и температуры на поверхностях трубы (t₁ иt₂).

Теплота от дымовых газов, содержащих в своем составе излучающие газы (СО₂ и Н₂О), к наружной поверхности трубы передается конвекцией ( ) и излучением (Q_л), через стенку трубы – теплопроводностью (Q_т), от внутренней поверхности трубы к воде – путем конвективного теплообмена ( ).

Таким образом, передаваемый тепловой поток

,	(5.13)
,	(5.14)
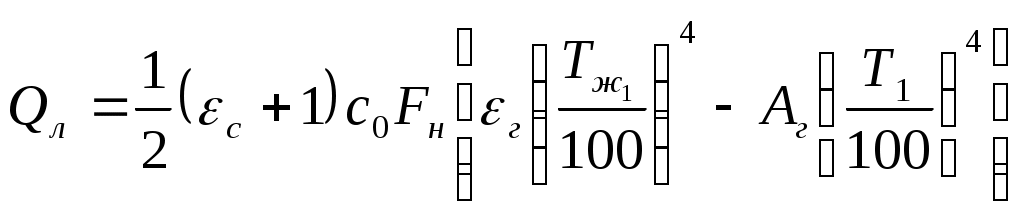,	(5.15)
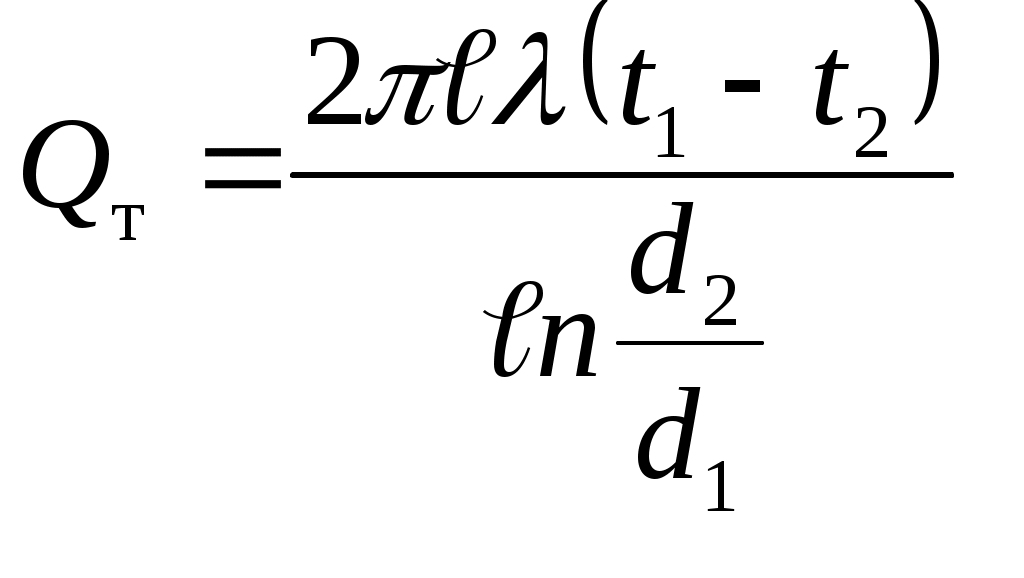,	(5.16)

---

,

(5.17)

где F_н = πd₂ , F_в = πd₁ - площади наружной и внутренней поверхностей трубы; ε_г, А_г – степень черноты и коэффициент поглощения газов (см. формулу 4.40).

Заменяя суммарную теплоотдачу от дымовых газов к поверхности трубы эквивалентным конвективным тепловым потоком

,

(5.18)

получим формулу для расчета эквивалентного коэффициента теплоотдачи

,

(5.19)

где , Вт/м² – плотность потока излучения.

Таким образом, приходим к системе трех уравнений:

,	(5.20)
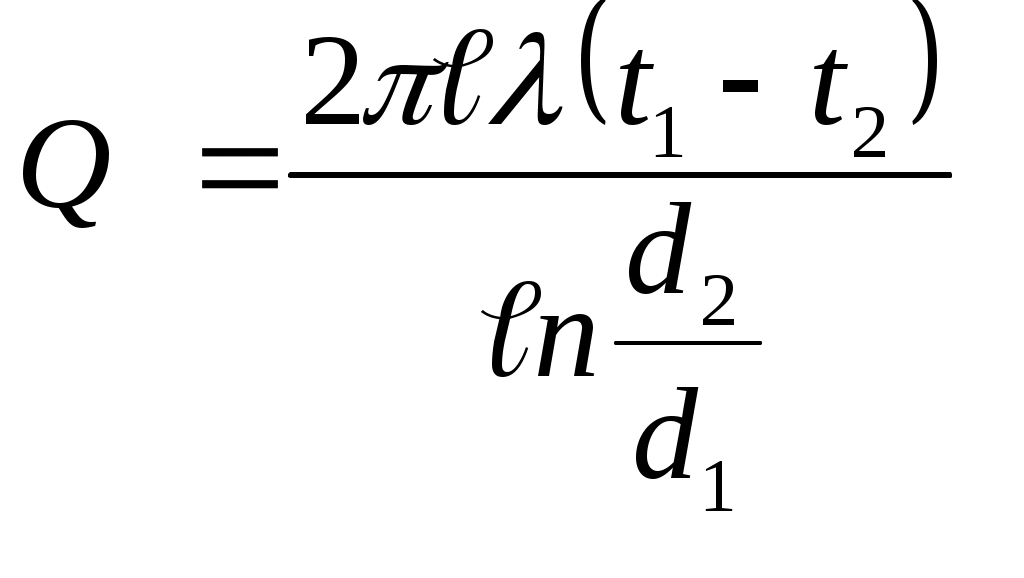,	(5.21)
,	(5.22)

совместное решение которых дает расчетную формулу для теплового потока

.

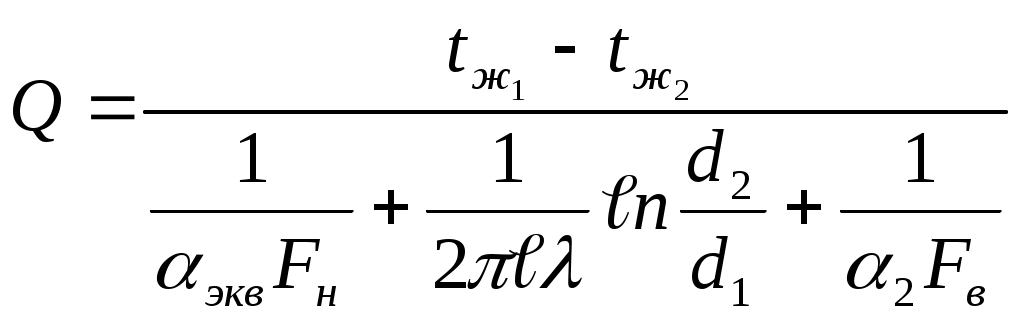(5.23)

А далее расчет производят по той же схеме: задают температуру на поверхности со сложным теплообменом t₁, рассчитывают α_экв, тепловой поток по формуле (5.23), сравнивают заданную температуру

---