Файл: Учебное пособие Томск 2001 удк.doc

t₁ с найденной температурой t₁ из уравнения (5.20). Повторяют расчет до их совпадения. Затем рассчитывают температуру t₂ по уравнениям (5.21) или (5.22).

---

5.3. Интенсификация теплопередачи

К ак известно, назначение тепловой изоляции – уменьшить передаваемую теплоту. Наряду с этим в технике приходится решать обратную задачу – увеличить теплопередачу. Примерами таких технических устройств являются теплообменники, токоведущие части электрических аппаратов и т.д.

Рассмотрим передачу теплоты от горячей воды с температурой к воздуху с температурой , через плоскую стенку толщиной δ с площадью поверхности F (рис. 5.3).

Передаваемый через стенку тепловой поток

,

(5.24)

прямо пропорционален коэффициенту теплопередачи



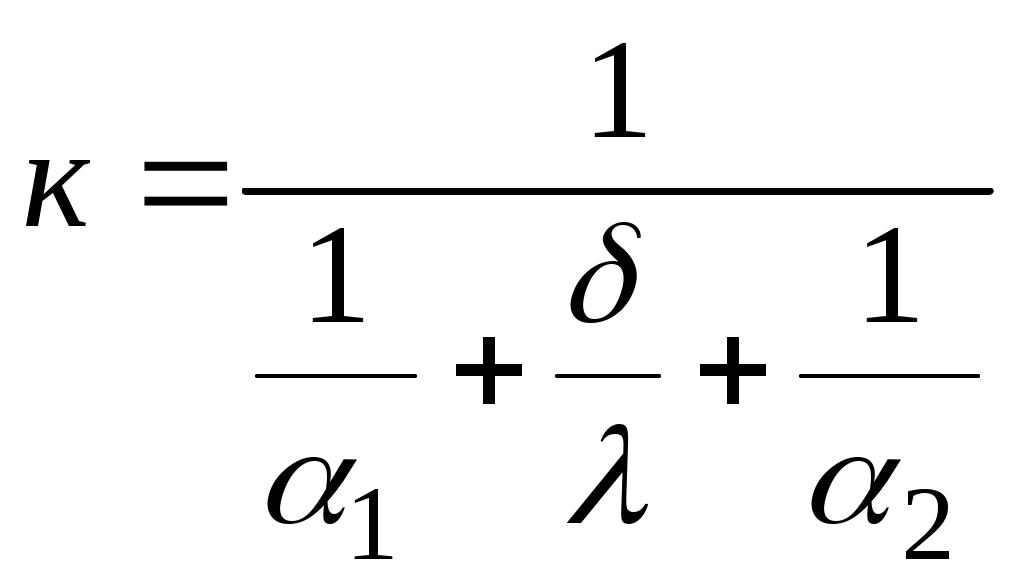
и обратно пропорционален сумме термических сопротивлений

.

Уменьшить термические сопротивления можно за счет увеличения коэффициентов теплоотдачи α₁ и α₂, уменьшения толщины стенки δ и увеличения коэффициента теплопроводности стенки (λ).

Если формулу (5.24) записать в виде

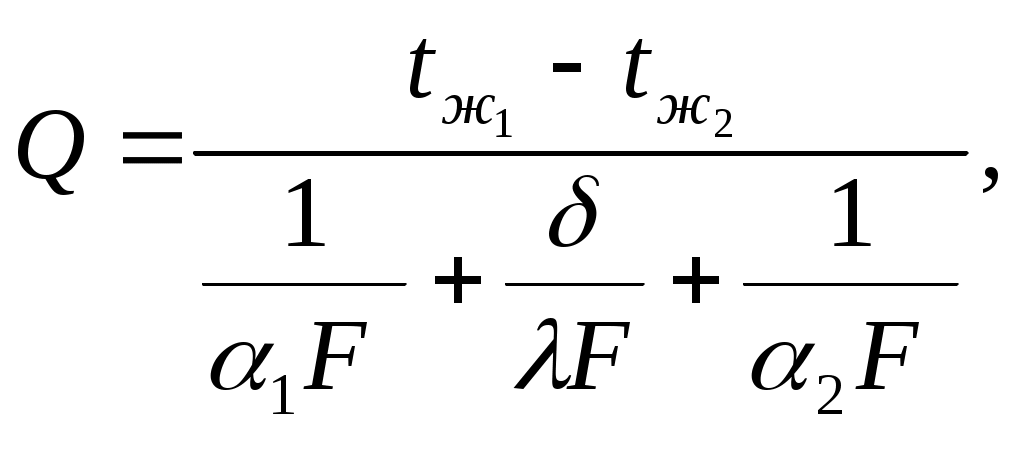(5.25)

то появится еще один способ уменьшения термических сопротивлений – увеличение площади поверхности теплообмена Fза счет оребрения стенки.

Именно этот способ чаще всего применяется для интенсификации теплопередачи.

Учитывая, что термическое сопротивление стенки мало , увеличивать площадь поверхности теплообмена следует со стороны меньшего коэффициента теплоотдачи. При α₁>> α₂ (рис. 5.3, теплоотдача от воды к стенке на 2 порядка больше, чем от стенки к воздуху) термическое сопротивление

---

, следовательно, теплопередачу (Q) определяет термическое сопротивление . Если оребрить поверхность стенки со стороны воздуха (рис.5.4), то термическое сопротивление уменьшится:

,

а теплопередача

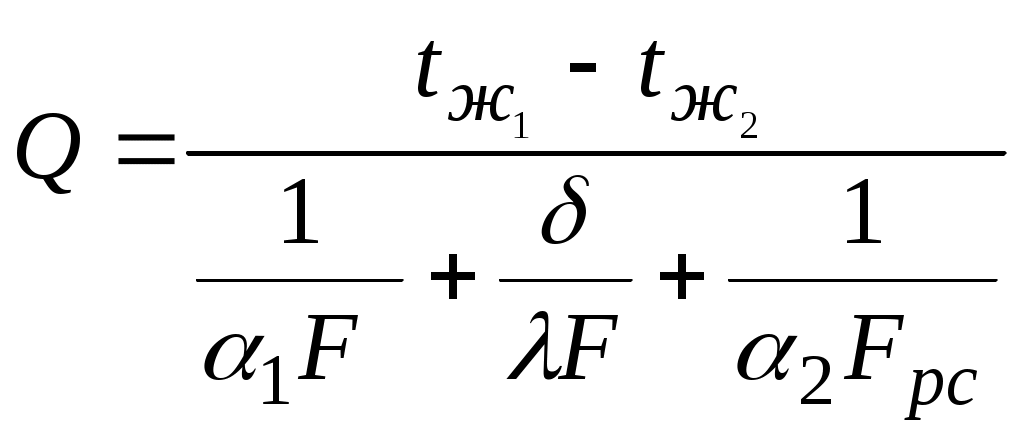(5.26)

увеличится.

Отношение называют коэффициентом оребрения. Увеличивать F_pc можно до тех пор, пока термическое сопротивление не сравняется с любым из двух других ( или ). Дальнейшее увеличение F_pc малоэффективно.

Формула (5.26) для расчета теплопередачи через оребренную стенку является приближенной, т.к. не учитывает форму, размеры, ориентацию ребер.

Расчетные уравнения для оребренных стенок можно получить, если рассмотреть задачу о теплопроводности стержня (ребра) постоянного поперечного сечения, нагреваемого с одного конца (рис. 5.5).

Т 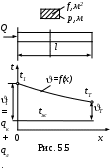онкий стержень с высокой теплопроводностью λ, длиной , поперечным сечением f(p– периметр сечения f), с температурой в начальном сечении t₁ находится в среде с постоянной температурой t_ж. Коэффициент теплоотдачи от поверхности стержня к окружающей среде – α .

Ввиду высокого коэффициента теплопроводности стержня и малых размеров сечения f по сравнению с длиной стержня , можно пренебречь изменением температуры по сечению и учитывать изменение температуры только по длине стержня.

Математическая формулировка задачи включает в себя дифференциальное уравнение температурного поля стержня (5.27) и граничные условия в начальном сечении(5.28) и на торце стержня (5.29)

---

	(5.27)
при x =0  = 1,	(5.28)
.	(5.29)

Здесь  = t - t_ж – избыточная температура стержня; ₁ = t₁ - t_ж – избыточная температура начального сечения стержня; , 1/м;
f, м² – площадь поперечного сечения стержня; р, м –периметр этого сечения.

Решением системы уравнений (5.27) – (5.29) является уравнение температурного поля стержня

,

(5.30)

по которому можно вычислить температуры на любой координате x по длине стержня (рис. 5.5). Закон распределения температуры по длине стержня =f(x) – степенной, т.к. гиперболические функции

,	(5.31)
,	(5.32)
	(5.33)

описываются степенными зависимостями.

На основании (5.30) при x= можно получить формулу для расчета избыточной температуры торца стержня _Т = t_T - t_ж

.

(5.34)

Количество теплоты, отдаваемое поверхностью стержня в окружающую среду, равно количеству теплоты, подводимой к основанию стержня,

---

(5.35)

Совместное решение (5.35) и (5.30) дает расчетную формулу для теплового потока, рассеиваемого стержнем

, Вт.

(5.36)

Формулы (5.30), (5.34), (5.36) применяются для расчета температуры и тепла, рассеиваемого ребрами.

5.3.1. Теплоотдача поверхности с прямыми ребрами

На рис. 5.6 показана стенка с прямыми горизонтальными ребрами.

Тепловой поток, рассеиваемый оребренной поверхностью, рассчитывается по формуле

,

(5.37)

где Q_p, Q_c – тепловые потоки, рассеиваемые одним ребром и межреберной поверхностью соответственно:

,	(5.38)
,	(5.39)

Обозначения: _р,_с – коэффициенты теплоотдачи от ребер и межреберной

поверхности соответственно; t_ж – температура среды;

t₁– температура межреберной поверхности и основания ребер;


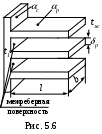
_р – толщина ребра; - длина ребра; b – ширина ребра;

F_c – площадь межреберной поверхности; n – число ребер

,

(5.40)

, .

---