Файл: Учебное пособие Томск 2001 удк.doc

Учитывая малую толщину ребер, можно принять р = 2b и тогда значение m, наряду с (5.40), можно рассчитывать по формуле (5.41)

(5.41)

Отношение теплового потока, рассеиваемого ребром (Q_p) к максимально возможному тепловому потоку ( ), при условии постоянной избыточной температуры по длине ребра (₁ = const), называют коэффициентом эффективности ребра и обозначают E:

,

(5.42)

где F_p = 2b , м² – площадь поверхности ребра.

После подстановки в (5.42) значений m, f, F_p и последующих алгебраических преобразований получим формулу для коэффициента эффективности ребра в виде

.

(5.43)

Анализ (5.43) дает, что E 1 при mℓ 0, т.е. чем меньше длина ребра ( ), чем больше его теплопроводность (λ), тем больше коэффициент эффективности ребра (Е).

На основании (5.42) можно записать формулу для теплового потока, рассеиваемого ребром, в виде

.

(5.44)

Избыточная температура торца прямого ребра рассчитывается по формуле (5.34).

5.3.2. Теплоотдача оребренных труб

Труба с прямыми продольными ребрами постоянного сечения (рис. 5.7)

В

---

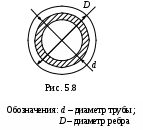
се расчеты производятся по вышеприведенным формулам для прямых ребер.
Труба с круглыми поперечными ребрами (рис. 5.8).

Тепловые потоки, рассеиваемые оребренной трубой (Q), межреберной поверхностью (Q_c) и круглым ребром (Q_p), рассчитываются по формулам (5.37), (5.39), (5.44), значение m – по формуле (5.41).

Коэффициент эффективности круглого ребра рассчитывается по уравнению

,

где - длина круглого ребра.

Площадь поверхности круглого ребра рассчитывается по формуле

.

Труба с поперечными прямоугольными ребрами (рис. 5.9)

Т 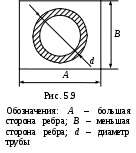епловые потоки Q,Q_c,Q_p и величина т рассчитываются по тем же формулам, что и для трубы с круглыми ребрами.

Коэффициент эффективности прямоугольного ребра рассчитывается по формуле

г

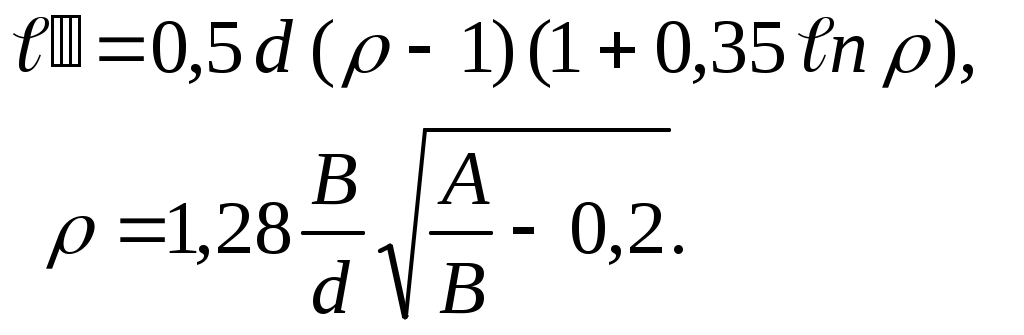
де

Площадь поверхности прямоугольного ребра определится по формуле

5.3.3. Теплопередача через оребренные стенки

Теплопередача от одной жидкости с к другой с через оребренную стенку рассчитывается по формулам:

• 
  д ля плоской стенки (рис. 5.10)
  

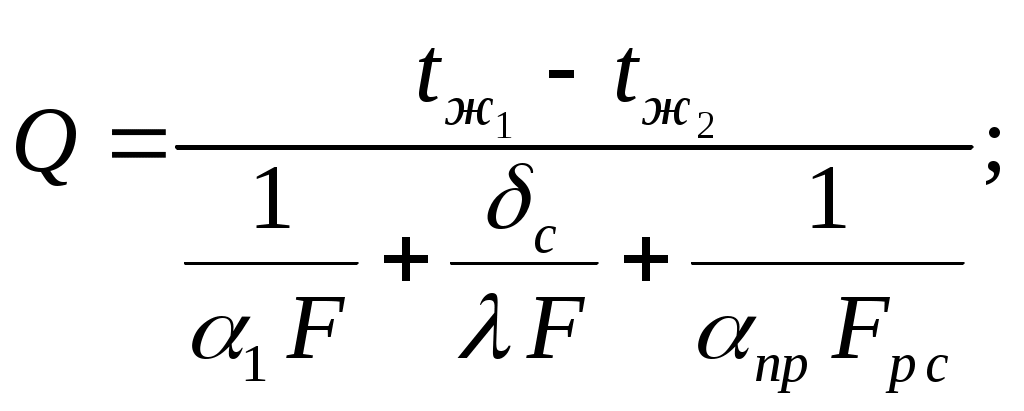
(5.45)

---

- для оребренной стенки трубы

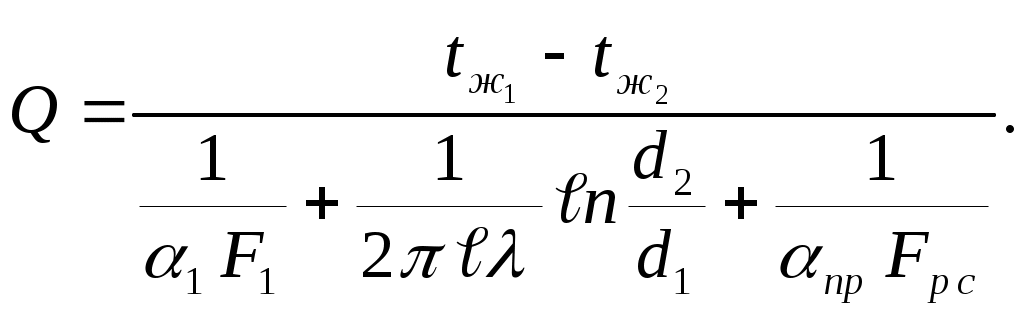
(5.46)

В формулах (5.45) и (5.46) приведенный коэффициент теплоотдачи (_пр) и площадь оребренной поверхности (F_pc) рассчитываются по формулам

,	(5.47)
,	(5.48)

где F_p – площадь поверхности ребра; n– число ребер.

Учитывая, что , в (5.47) можно принять α_с = α_p.

Контрольные вопросы и задания

1. 
   Дайте определение эквивалентного коэффициента теплоотдачи (формула 5.8) "Эквивалентный коэффициент теплоотдачи – это …". Закончите фразу.
   
2. 
   От наружной поверхности трубы диаметром d= 50 мм с температурой t_с = 90С теплота передается к окружающему спокойному воздуху с температурой t_ж = 10С. Конвективный коэффициент теплоотдачи
   = 8 Вт/м²К. Степень черноты поверхности трубы _с= 0,9.
   

Рассчитайте лучистый (_л) и эквивалентный (_экв) коэффициенты теплоотдачи.

3. 
   Для условия предыдущей задачи сравните конвективный () и лучистый (_л) коэффициенты теплоотдачи. Как изменится соотношение между ними:
   

а) при уменьшении температуры поверхности трубы до t_c = 40С;

б) при увеличении температуры до t_с = 120С?

Сделайте выводы.

4. 
   По виду теплоносителей различают теплообменники водо-водяные, газо-водяные, газо-газовые. В каких теплообменниках и со стороны какого теплоносителя выполняется оребрение?
   
5. 
   Поясните физический смысл коэффициента эффективности ребра. При каких условиях он растет?
   
6. 
   Батарея отопления – чугунная труба с поперечными круглыми ребрами. Длина трубы _тр=1м, наружный диаметр трубы d = 60 мм, число ребер n = 50, диаметр ребер D = 120 мм, толщина ребер δ = 2 мм.
   

---

Рассчитайте площадь оребренной поверхности (F_pc).

7. 
   Батарея отопления – чугунная труба с поперечными круглыми ребрами.
   

Дано: длина трубы ( _тр), наружный диаметр трубы (d), толщина ребер и их количество (δ_р, п), диаметр ребер (D), теплопроводность чугуна (λ), температура наружной поверхности трубы (t_с),температура окружающей среды (t_ж), коэффициенты теплоотдачи от межреберной поверхности (_с) и от ребер (_р).

Запишите все формулы, необходимые для расчета конвективной теплоотдачи (Q, Вт) от поверхности оребренной трубы.

Примеры решения задач

Задача №1. Рассчитать плотность теплового потока (q, Вт/м²), передаваемого через чугунную стенку трубы батареи отопления от горячей воды с температурой к спокойному окружающему воздуху с температурой , и температуры на поверхностях стенки (t₁ и t₂).

Толщина стенки трубы, коэффициент теплопроводности чугуна и степень черноты поверхности трубы равны соответственно δ_с=3мм,
λ = 63 Вт/м· К, _с= 0,9. Конвективный коэффициент теплоотдачи от воды к внутренней поверхности ₁ = 3500 Вт/м²· К, от наружной поверхности стенки трубы к воздуху ₂ = 6,5 Вт/м² К.
Решение

Для металлических труб, вследствие их высокой теплопроводности, пренебрегают кривизной стенки и расчет производят по формулам для плоской стенки. В этом случае расчетные уравнения для данной задачи обозначены номерами (5.5), (5.7), (5.9)-(5.12).

На наружной поверхности трубы – сложный теплообмен. Задаемся температурой этой поверхности. Пусть t₂ = 69°С.

Рассчитываем

,

---

,

.

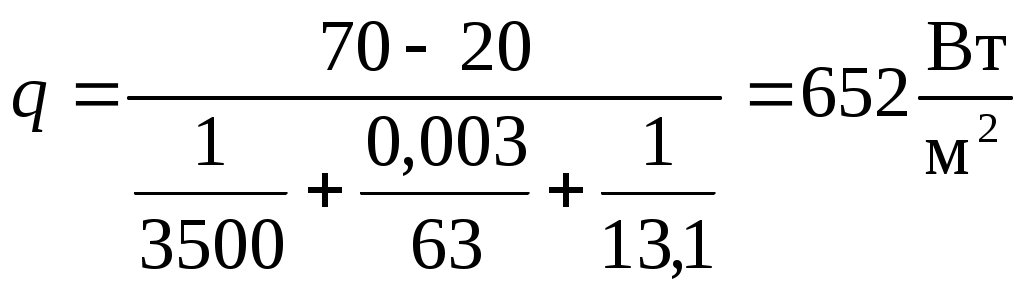Из уравнения (5.11) находим температуру t₂:

.

Отличие найденной температуры t₂от заданной составляет 0,77°С, т.е. меньше одного градуса, и повторение расчета при t₂ = 69,77°С практически не изменит величину q= 652 Вт/м².

Определим температуру на внутренней поверхности трубы по формуле (5.10):



Ответы: q = 652 Вт/м² , t₁ = 69,8°С, t₂ = 69,77°С.
Задача №2. Водяной экономайзер выполнен из круглых ребристых чугунных труб наружным диаметром d= 76 мм. Диаметр ребер D = 200 мм, толщина ребер δ_р=5 мм.

Определить количество теплоты, которое будет передаваться от горячих газов к наружной поверхности одной трубы, и температуру на торце ребра, если температура газов t_ж = 400°С, температура у основания ребер t₁ = 180°С, длина обогреваемой части трубы _тр= 3 м, количество ребер n= 150. Коэффициент теплоотдачи от газов к оребренной поверхности α=46,5 Вт/м² К, коэффициент теплопроводности чугуна λ =52,4 Вт/м К.

Решение

Для определения теплового потока, воспринимаемого круглым ребром (Q_p), необходимы следующие величины:

,

,

,

,

,

---