ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 639
Скачиваний: 3
СОДЕРЖАНИЕ
1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
1.2. Температурное поле. Градиент температуры. Тепловой поток
1.4. Дифференциальное уравнение теплопроводности
2. ТЕПЛОПРОВОДНОСТЬ И ТЕПЛОПЕРЕДАЧА ПРИ СТАЦИОНАРНОМ РЕЖИМЕ
2.1. Теплопроводность плоской стенки при граничных условиях первого рода
2.2. Теплопроводность цилиндрической стенки при граничных условиях первого рода
2.4. Критический диаметр тепловой изоляции
3. ТЕПЛОПРОВОДНОСТЬ ТЕЛ С ВНУТРЕННИМИ ИСТОЧНИКАМИ ТЕПЛАПРИ СТАЦИОНАРНОМ РЕЖИМЕ
3.1. Теплопроводность однородной пластины
3.2. Теплопроводность однородного цилиндрического стержня
3.3. Теплопроводность цилиндрической стенки
4.1. Теплообмен излучением между твердыми телами, разделенными диатермичной средой
4.2. Особенности излучения газов
5.1. Теплопередача через плоскую стенкусо сложным теплообменом
5.2. Теплопередача через цилиндрическую стенкусо сложным теплообменом
5.3. Интенсификация теплопередачи
6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ТЕПЛООБМЕНАИ ОСНОВЫ ТЕОРИИ ПОДОБИЯИ МОДЕЛИРОВАНИЯ ПРОЦЕССОВ
6.1. Дифференциальные уравнения теплообмена
6.3. Моделирование теплоотдачи
6.4. Физические особенности процесса теплоотдачи
7. ТЕПЛООТДАЧА В ОДНОФАЗНОЙ СРЕДЕ
7.1. Теплоотдача при свободном движении жидкости
7.2. Теплоотдача при продольном омывании поверхности вынужденным потоком жидкости
7.3. Теплоотдача при вынужденном течении жидкости в трубах и каналах
7.4. Теплоотдача при поперечном обтекании труб
8. ТЕПЛООТДАЧА ПРИ ФАЗОВЫХ ПРЕВРАЩЕНИЯХ
8.2. Теплоотдача при конденсации
9.1. Классификация теплообменников
Тогда
Площадь межреберной поверхности
Тепловой поток, воспринимаемый межреберной поверхностью,
Тепловой поток, передаваемый от горячих газов к оребренной трубе,
Для определения температуры торца ребра рассчитаем
Тогда
Ответы: Q= 53,8 кВт, tт = 311,8С.
6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ТЕПЛООБМЕНА
И ОСНОВЫ ТЕОРИИ ПОДОБИЯ
И МОДЕЛИРОВАНИЯ ПРОЦЕССОВ
6.1. Дифференциальные уравнения теплообмена
В общем случае теплообмен определяется не только тепловыми, но и гидродинамическими явлениями. Поэтому математическое описание задач теплообмена включает в себя дифференциальные уравнения:
-
энергии; -
теплоотдачи; -
движения; -
неразрывности,
а также условий однозначности, конкретизирующих ту или иную задачу.
Дифференциальное уравнение температурного поля движущейся жидкости – уравнение энергии(1.12) – приведено в разделе 1.
Уравнение теплоотдачи. При обтекании вязкой жидкостью твердой поверхности скорость жидкости на ней равна нулю. Это условие «прилипания» вязкой жидкости является следствием того, что между поверхностью твердого тела и жидкостью действуют силы молекулярного сцепления, в результате чего прилегающий к твердой стенке слой жидкости становится неподвижным и теплота через этой слой передается только теплопроводностью
С другой стороны, этот же тепловой поток определяется уравнением Ньютона-Рихмана
Приравняв правые части равенств, получим дифференциальное уравнение теплоотдачи
| | (6.1) |
из которого следует, что для определения коэффициента теплоотдачи необходимо найти температурный градиент среды вблизи поверхности. Температурный градиент может быть найден из дифференциального уравнения энергии (1.12). В уравнение (1.12) входят составляющие скорости (wx, wy , wz), которые требуют дифференциального уравнения, позволяющего найти поле скоростей, – уравнения движения.
Уравнение движения. В классической гидродинамике уравнение движения вязкой несжимаемой жидкости (уравнение Навье – Стокса) для стационарного режима в проекции на ось
ох имеет вид
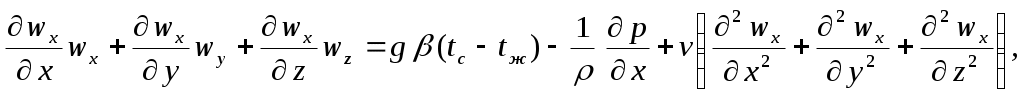 (6.2)
(6.2)где wx – проекция вектора скорости на ось ох; g=9,8 м/с2 ;
р, Па – давление; v, м2/с – кинематическая вязкость.
Левая часть уравнения (6.2) характеризует инерционные силы потока жидкости, первое слагаемое правой части определяет подъемную силу, возникающую вследствие разности плотностей холодных и нагретых объемов жидкости, второе слагаемое – действие сил давления, третье – сил вязкого трения.
Аналогичные уравнения в проекции на оси оy, оz обозначим номерами (6.3), (6.4).
Анализ уравнений (1.12), (6.1) – (6.4) показывает, что для решения задачи конвективного теплообмена к перечисленным выше уравнениям необходимо добавить еще одно – уравнение неразрывности потока.
Уравнение неразрывности. Применение закона сохранения массы к элементарному объему несжимаемой жидкости дает дифференциальное уравнение неразрывности
| | (6.5) |
Условия однозначности включают:
-
геометрические условия (форму и размеры поверхности соприкосновения с жидкостью); -
физические условия (теплопроводность, вязкость и др. свойства жидкости); -
граничные условия (распределение скоростей и температур на границах рассматриваемой системы).
Для некоторых задач теплообмена могут быть получены и более сложные системы дифференциальных уравнений и условий однозначности.
Решение системы дифференциальных уравнений конвективного теплообмена возможно при введении упрощающих предположений для некоторых случаев теплоотдачи. Однако принятые допущения требуют сопоставления аналитических решений с результатами эксперимента.
В ряде случаев система дифференциальных уравнений конвективного теплообмена решается численными методами с применением ЭВМ.
В большинстве же случаев единственным способом получения уравнения для расчета коэффициента теплоотдачи является физический эксперимент с обработкой данных на основе теории подобия физических явлений.
6.2. Основы теории подобия
Теория подобия – учение о подобных явлениях. Она позволяет на основе дифференциальных уравнений и условий однозначности создать теоретическую базу для постановки опытов и обработки их результатов.
Понятие подобия впервые было введено в геометрии, но оно распространяется и на физические явления. Последние считаются подобными, если они относятся к одному и тому же классу, протекают в геометрически подобных системах и подобны все однородные физические величины, характеризующие эти явления.
Для подобных физических явлений в сходственных точках и в сходственные моменты времени любая величина φ первого явления пропорциональна величине второго явления: φ=Сφ ∙ φ, где Сφ – константа подобия. Два промежутка времени τ′ и τ" называются сходственными, если они имеют общее начало отсчета и связаны равенством τ′ / τ"=Сτ=const. При геометрическом подобии выполняется равенство
| х′ / х"=у' / у"=z' / z"= |
При кинематическом подобии имеет место подобие скоростей w′/w′′=Cw, при динамическом – подобие сил давления р′ /р"=СР , при тепловом – подобие температурных полей t'/t"=Ct .
Для физических явлений, определяемых множеством параметров, константы подобия этих параметров связаны между собой и не могут быть выбраны произвольно.
Уравнения, описывающие подобные физические явления, после приведения их к безразмерному виду становятся тождественными, при этом в сходственных точках все одноименные безразмерные величины будут одинаковыми.
Приведение к безразмерному виду системы дифференциальных уравнений конвективного теплообмена (1.12), (6.1) – (6.5)