Файл: Учебное пособие Томск 2001 удк.doc

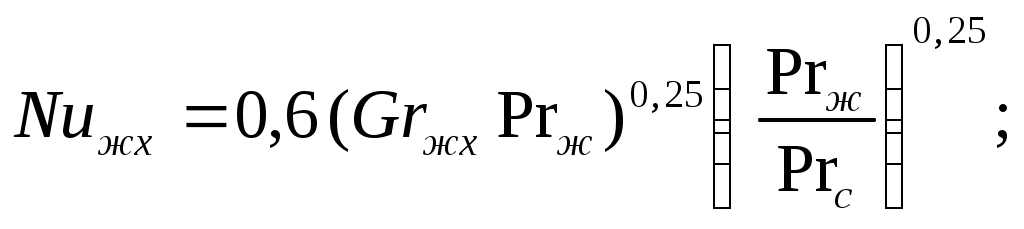(7.3)

средние коэффициенты теплоотдачи на участке поверхности высотой ℓ с ламинарным течением в пограничном слое – по уравнению

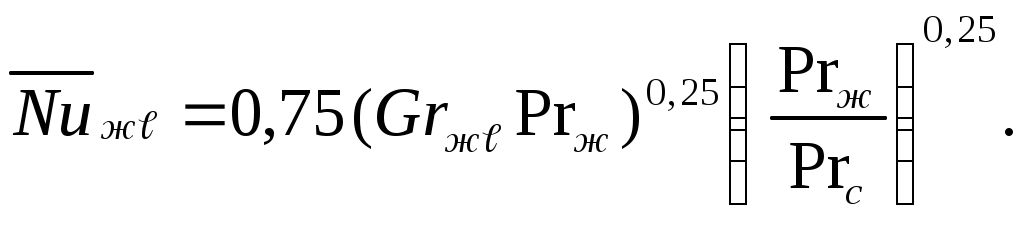(7.4)

• 
  При турбулентном режиме, (Gr_жх∙Pr_ж)>6 10¹⁰, коэффициенты теплоотдачи рассчитываются по уравнению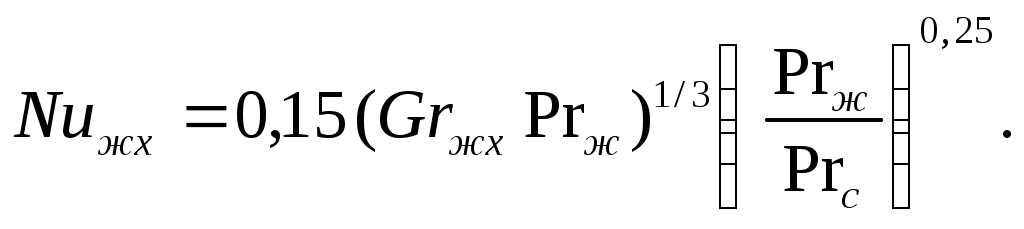
  

  (7.5)

• 
  При переходном режиме, 10⁹<(Gr_жх∙Pr_ж)<6∙10¹⁰, средний коэффициент теплоотдачи можно определить по формуле
  

(7.6)

где рассчитывается по уравнению (7.5), - по (7.3).

Коэффициент теплоотдачи зависит от направления теплового потока, и обусловлено это неодинаковыми средними температурами жидкости вблизи поверхности при нагреве жидкости (t_c>t_ж) и при охлаждении (t_cж), а также зависимостью теплофизических свойств жидкости от ее температуры. Как следствие этого, коэффициент теплоотдачи капельных жидкостей при нагреве больше, чем при охлаждении. Влияние указанного фактора учитывается в уравнениях подобия сомножителем (Pr_ж /Pr_c)^0,25.

При нагреве жидкости (t_c>t_ж) — (Pr_ж /Pr_c)^0,25>1, при охлаждении
(t_cж) — (Pr_ж /Pr_c)^0,25<1. Числа Pr_ж и Pr_c берутся из справочных таблиц для жидкости в первом случае – по t_ж, во втором — по t_с.

Для газов с достаточной точностью можно считать, что сомножитель
(Pr_ж /Pr_c)^0,25=1.

Форма поверхности при естественной конвекции жидкости играет второстепенную роль (важна ее протяженность), поэтому по вышеприведенным формулам рассчитывается теплоотдача от плоских, цилиндрических или иной формы вертикальных поверхностей.

Приведенные выше формулы применимы и для горизонтальных плит, но в этом случае вычисленный коэффициент теплоотдачи надо увеличить на 30%, если теплоотдающая поверхность плиты обращена вверх, и уменьшить на 30%, если теплоотдающая поверхность обращена вниз. В качестве определяющего размера берется меньшая сторона плиты.

Для горизонтальных труб, если10³<(Gr_жd∙Pr_ж) 10⁹, для расчета средних коэффициентов теплоотдачи рекомендуется следующее уравнение:

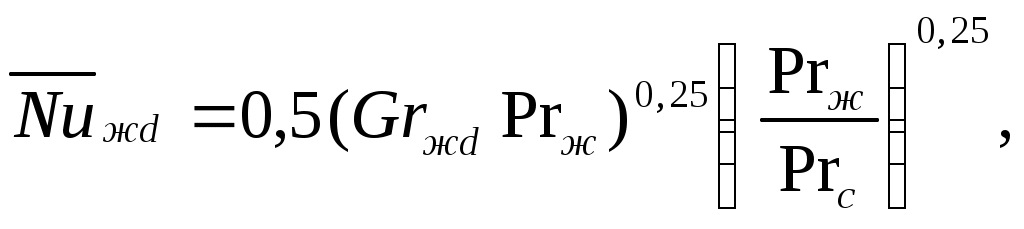(7.7)

определяющий размер – наружный диаметр трубы (d).

Рассмотренная картина движения жидкости относится к случаям, когда расположение и размеры поверхностей, замыкающих среду, на развитие свободного движения не влияют. Такое движение называется свободной конвекцией в большом объеме.

Естественная конвекция в ограниченном объеме характеризуется наличием восходящих и нисходящих потоков, когда условия свободного движения жидкости значительно отличаются от ее движения в неограниченном пространстве.

Примеры естественной конвекции жидкости в ограниченном объеме представлены на рис. 7.2

а
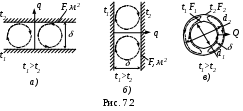
) горизонтальная прослойка жидкости или газа;

б) вертикальная прослойка;

в) цилиндрическая (или сферическая) прослойка
Через газовые прослойки передача теплоты между поверхностями осуществляется тремя способами: теплопроводностью, конвекцией и излучением,через прослойки капельной жидкости – двумя: теплопроводностью и конвекцией. Во всех случаях передачу теплоты рассчитывают по формулам теплопроводности, но коэффициент теплопроводности среды заменяют эквивалентным, учитывающим перенос теплоты другими способами.

Для плоских прослоек тепловой поток рассчитывают по уравнению

Вт,

(7.8)

для цилиндрических

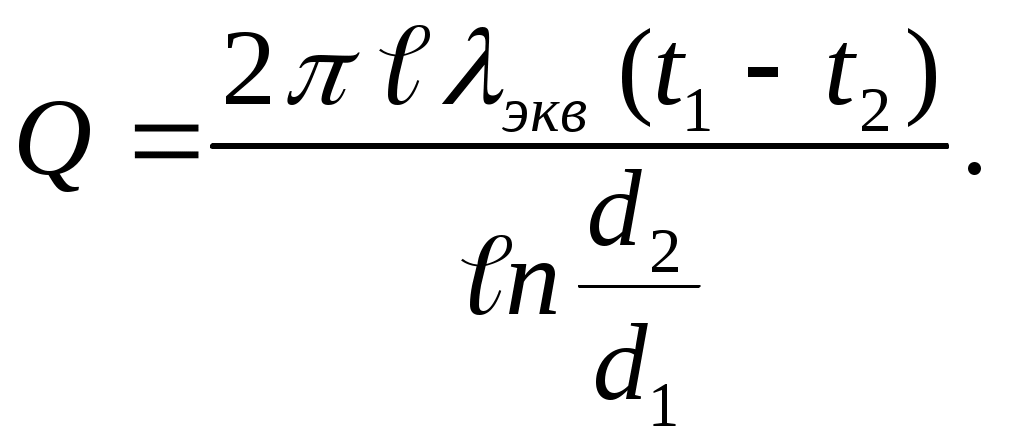(7.9)

Для прослоек капельной жидкости

(7.10)

где λ –коэффициент теплопроводности жидкости; ε_к – коэффициент, учитывающий перенос тепла конвекцией.

Для прослоек любой формы при (Gr_жδ ∙Pr_ж)>10³ коэффициент конвекции рассчитывается по формуле

(7.11)

где определяющая температура

При (Gr_жδ∙Pr_ж)<10³ принимают ε_к=1.

Для газовых плоских прослоек

(7.12)

где q_л, Вт/м² – плотность теплового потока, передаваемого излучением через газовую прослойку.

Для газовых цилиндрических прослоек

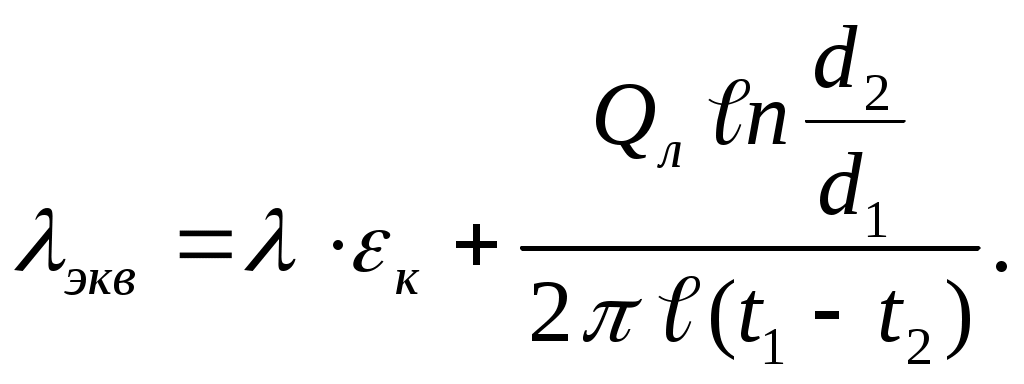(7.13)

1   ...   15   16   17   18   19   20   21   22   ...   28

---

7.2. Теплоотдача при продольном омывании поверхности
вынужденным потоком жидкости

Вынужденное течение жидкости (вынужденная конвекция) возникает под действием разности давлений, которая в совокупности с теплофизическими свойствами определяет скорость движения жидкости w₀. Таким образом, при вынужденном движении определяющими числами подобия являются число Рейнольдса (Re), включающее в себя скорость w₀, и число Прандтля (Pr), зависящее от теплофизических свойств жидкости,

В некоторых случаях при малых скоростях и больших температурных напорах (t_c-t_ж) на вынужденное течение жидкости могут накладываться токи естественной конвекции, и тогда

Nu=f(Re, Gr, Pr).

Рассмотрим участок поверхности, имеющий температуру t_c и омываемый потоком жидкости с температурой t_ж и скоростью w₀. Вблизи поверхности формируется гидродинамический пограничный слой (δ) с ламинарным, переходным и турбулентным режимами течения (рис. 7.3)

Р 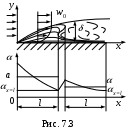ежим течения в гидродинамическом пограничном слое определяется числом Рейнольдса

При Re_жх<10⁴ – ламинарный режим;

при Re_жх>4∙10⁶ – турбулентный;

при 10⁴ <Re_жх<4∙10⁶ – переходный.

Для переходного режима из-за неустойчивого течения, характеризуемого частой сменой во времени ламинарного и турбулентного режимов, отсутствует методика расчета коэффициентов теплоотдачи, поэтому его исключают и считают, что

---

при Re_жх 5∙10⁵ – ламинарный режим в пограничном слое;

при Re_жх>5∙10⁵ – турбулентный режим.

В учебной литературе для вынужденного течения жидкости около поверхности приводится вывод интегральных уравнений для теплового и гидродинамического пограничных слоев:

	(7.14)
	(7.15)

Если воспользоваться этими уравнениями для ламинарного и турбулентного режимов течения в пограничном слое, то удается аналитически получить расчетные уравнения для коэффициентов теплоотдачи, которые хорошо согласуются с экспериментальными данными.

Вот эти уравнения для расчета локальных коэффициентов теплоотдачи:

– при ламинарном режиме течения жидкости в пограничном слое

Nuх=0,33 Reх0,5∙ Pr0,33,

(7.16)

– при турбулентном режиме

Nuх=0,0296 Reх0,8∙ Pr0,43.

(7.17)

Если подставить значения чисел подобия в (7.16),

и определить зависимость обозначив постоянной С все величины, кроме координаты х,

(7.18)

то можно найти средний коэффициент теплоотдачи для участка поверхности длиной с ламинарным течением в пограничном слое по формуле

(7.19)

---

Сравнивая (7.18) и (7.19), видим, что средний коэффициент теплоотдачи в
2 раза больше, чем локальный при х= , т.е.

Аналогичный анализ уравнения (7.17) дает, что



Графическое подтверждение см. на рис. 7.3. Коэффициент теплоотдачи при ламинарном режиме течения жидкости в пограничном слое с увеличением х убывает более резко, чем при турбулентном режиме.

Таким образом, теоретические и экспериментальные исследования позволили получить следующие уравнения для расчета средних коэффициентов теплоотдачи для участка поверхности длиной при наличии ламинарного пограничного слоя (Re_жℓ 5∙10⁵):

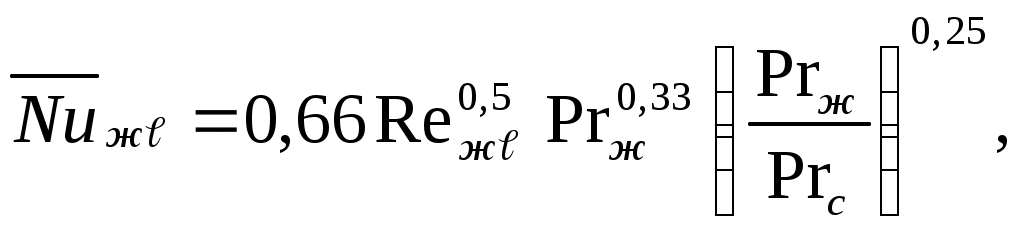(7.20)

турбулентного пограничного слоя (Re_жℓ >5∙10⁵):

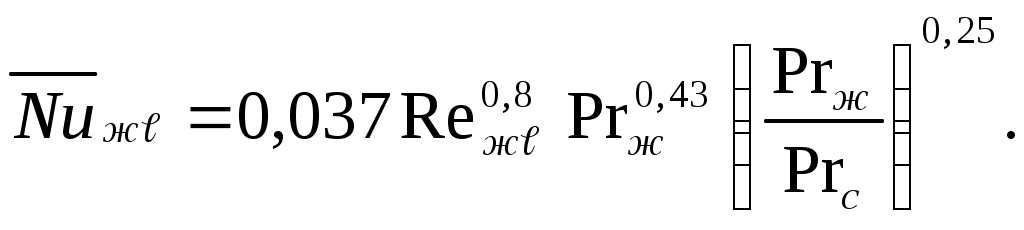(7.21)

Форма поверхности (плоская, цилиндрическая или иная) при продольном омывании её вынужденным потоком жидкости не влияет на коэффициент теплоотдачи.

---

7.3. Теплоотдача при вынужденном течении жидкости
в трубах и каналах

П
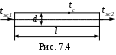
ри течении в трубе (рис. 7.4) жидкость может нагреваться или охлаждаться.

П
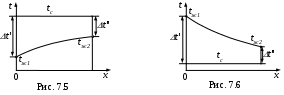
ри нагреве: где - средняя температура жидкости на участке трубы длиной (рис. 7.5). При охлаждении: (рис.7.6).

Уравнение теплового баланса для отрезка трубы длиной ℓ при нагреве жидкости

(7.22)

при охлаждении жидкости

(7.23)

Здесь расход жидкости; средняя по сечению трубы скорость; ρ, кг/м³, с_р, Дж/кг∙К – плотность и теплоемкость жидкости; f=πd²/4, м² – площадь поперечного сечения трубы; d, м – внутренний диаметр трубы;
Вт/м²∙К – коэффициент теплоотдачи между поверхностью трубы и жидкостью; F= πd , м² – площадь поверхности теплообмена между жидкостью и трубой.

Расчет средней температуры жидкости ( ).

Если через Δt΄и Δt" обозначить средние температурные напоры на входе и на выходе из трубы (рис.7.5 и 7.6), то

---