Файл: Учебное пособие Томск 2001 удк.doc

_ср в интервале температур t₁ - t₂, нетрудно получить, если решить совместно (1.6) и (1.7):

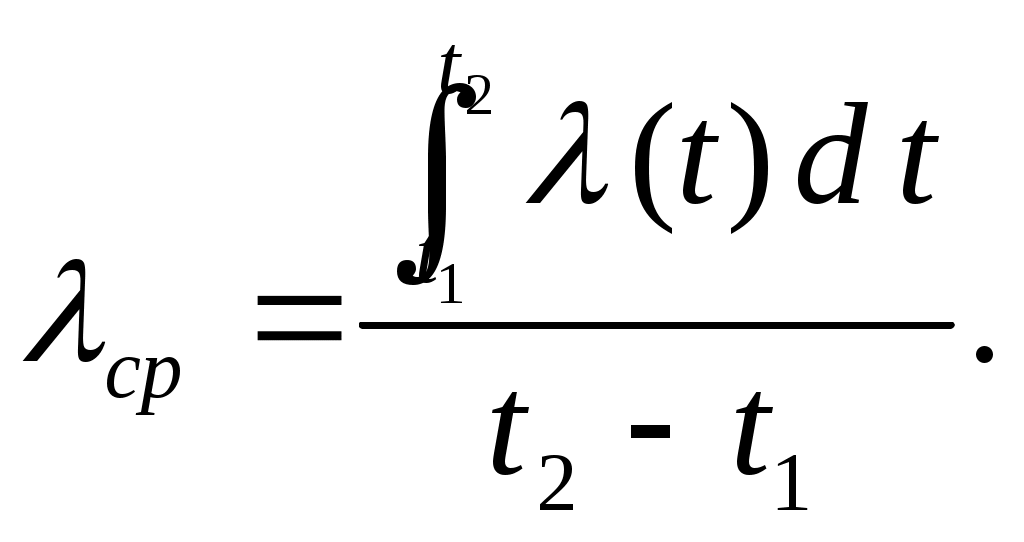	(1.7)
Тогда
	(1.8)

Такой прием можно применить для получения расчетных формул _ср при любой нелинейной зависимости (t).

Конвективную теплоотдачу между поверхностью с температурой t_c и омывающей ее средой с температурой t_ж описывает закон Ньютона-Рихмана, согласно которому плотность теплового потока q пропорциональна разности температур стенки и среды:

(1.9)

По формулам (1.4) и (1.5) можно вычислить Q и Q_ .

Коэффициент пропорциональности в уравнении (1.9) называется коэффициентом теплоотдачи и характеризует интенсивность процесса конвективного теплообмена между поверхностью и омывающей ее средой. Принято омывающую поверхность среду (газ, воду, любой теплоноситель) именовать "жидкость" и обозначать температуру среды - t_ж.

Коэффициент теплоотдачи зависит от температур t_c и t_ж, от скорости и от свойств жидкости, от формы, размеров, ориентации поверхности и т.д. Коэффициенты теплоотдачи для различных условий теплообмена рассчитываются по специальным уравнениям.

Интегральная плотность теплового потока при переносе теплоты излучением рассчитывается по формуле

(1.10)

В уравнении (1.10) коэффициентом пропорциональности является степень черноты излучающего тела (), которая характеризует его способность излучать и поглощать энергию. Для твердых тел значения  приводятся в справочниках, для излучающих газов - рассчитываются с помощью номограмм.

---

Выражение

(1.11)

известно как закон Стефана – Больцмана, описывающий связь плотности теплового потока и температуры абсолютно черного тела. Коэффициент излучения абсолютно черного тела с₀ = 5,67 Вт/(м² К⁴).

---

1.4. Дифференциальное уравнение теплопроводности

В учебниках по теплопередаче, в том числе и в [1], приводится вывод дифференциального уравнения температурного поля движущейся жидкости, уравнение энергии

(1.12)

где с_р, Дж/(кгК) – изобарная теплоемкость; , кг/м³ – плотность; , Вт/(мК) – коэффициент теплопроводности; _х, _y, _z – проекции вектора скорости движения жидкости; q_v , Вт/м³ – объемная плотность внутреннего тепловыделения жидкости.

Уравнение (1.12) записано для случая =const.

Дифференциальное уравнение температурного поля для твердых тел называется дифференциальным уравнением теплопроводности и может быть получено из (1.12) при условии _х= _y= _z=0, с_р= с_v=с:

,

где - коэффициент температуропроводности, характеризует скорость изменения температуры в теле. Значения а = f (t) для различных тел приводятся в справочниках.

Дифференциальное уравнение теплопроводности

(1.13)

описывает нестационарное температурное поле твердых тел с внутренним тепловыделением (с внутренними источниками тепла). Такими источниками тепла могут быть: джоулева теплота, выделяемая при прохождении электрического тока по проводникам; теплота, выделяемая ТВЭЛами ядерных реакторов и т.д.

Дифференциальное уравнение теплопроводности (1.13), записанное в декартовых координатах, можно представить в цилиндрических (r, z, φ) и сферических (r, φ, ψ).

В частности, в цилиндрических координатах (

---

r –радиус; φ – полярный угол; z - аппликата) дифференциальное уравнение теплопроводности имеет вид

(1.14)

1.5. Условия однозначности

Дифференциальное уравнение описывает множество процессов теплопроводности. Чтобы выделить из этого множества конкретный процесс, необходимо сформулировать особенности этого процесса, которые называются условиями однозначности и включают в себя:

• 
  геометрические условия, характеризующие форму и размеры тела;
  
• 
  физические условия, характеризующие свойства участвующих в теплообмене тел;
  
• 
  граничные условия, характеризующие условия протекания процесса на границе тела;
  
• 
  начальные условия, характеризующие начальное состояние системы при нестационарных процессах.
  

При решении задач теплопроводности различают:

• 
  граничные условия первого рода, когда задается распределение температуры на поверхности тела:
  

t_c = f (x, y, z, τ) или t_c =const;

• 
  граничные условия второго рода, когда задается плотность теплового потока на поверхности тела:
  

q_c = f (x, y, z, τ) или q_c =const;

• 
  граничные условия третьего рода, когда задается температура среды t_ж и коэффициент теплоотдачи между поверхностью и средой.
  

В соответствии с законом Ньютона-Рихмана тепловой поток, передаваемый с 1м² поверхности в среду с температурой t_ж,



В то же время этот тепловой поток подводится к 1м² поверхности из глубинных слоев тела теплопроводностью



Тогда уравнение теплового баланса для поверхности тела запишется в виде

(1.15)

Уравнение (1.15) является математической формулировкой граничных условий третьего рода.

---

Система дифференциальных уравнений совместно с условиями однозначности представляет собой математическую формулировку задачи. Решения дифференциальных уравнений содержат константы интегрирования, которые определяются с помощью условий однозначности.

Контрольные вопросы и задания

1. 
   Проанализируйте, какими способами передается теплота от горячей воды к воздуху через стенку батареи отопления: от воды к внутренней поверхности, через стенку, от наружной поверхности к воздуху.
   
2. 
   Почему в правой части уравнения (1.3) стоит минус?
   
3. 
   Проанализируйте с помощью справочной литературы зависимость λ(t) для металлов, сплавов, теплоизоляционных материалов, газов, жидкостей и ответьте на вопрос: как изменяется коэффициент теплопроводности с изменением температуры для этих материалов?
   
4. 
   Как определяется тепловой поток (Q, Вт) при конвективной теплоотдаче, теплопроводности, тепловом излучении?
   
5. 
   Запишите дифференциальное уравнение теплопроводности в декартовых координатах, описывающее трехмерное стационарное температурное поле без внутренних источников теплоты.
   
6. 
   Запишите дифференциальное уравнение температурного поля проволоки, которая длительное время находится под напряжением при постоянной электрической нагрузке.
   

---