ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 646
Скачиваний: 3
СОДЕРЖАНИЕ
1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
1.2. Температурное поле. Градиент температуры. Тепловой поток
1.4. Дифференциальное уравнение теплопроводности
2. ТЕПЛОПРОВОДНОСТЬ И ТЕПЛОПЕРЕДАЧА ПРИ СТАЦИОНАРНОМ РЕЖИМЕ
2.1. Теплопроводность плоской стенки при граничных условиях первого рода
2.2. Теплопроводность цилиндрической стенки при граничных условиях первого рода
2.4. Критический диаметр тепловой изоляции
3. ТЕПЛОПРОВОДНОСТЬ ТЕЛ С ВНУТРЕННИМИ ИСТОЧНИКАМИ ТЕПЛАПРИ СТАЦИОНАРНОМ РЕЖИМЕ
3.1. Теплопроводность однородной пластины
3.2. Теплопроводность однородного цилиндрического стержня
3.3. Теплопроводность цилиндрической стенки
4.1. Теплообмен излучением между твердыми телами, разделенными диатермичной средой
4.2. Особенности излучения газов
5.1. Теплопередача через плоскую стенкусо сложным теплообменом
5.2. Теплопередача через цилиндрическую стенкусо сложным теплообменом
5.3. Интенсификация теплопередачи
6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ТЕПЛООБМЕНАИ ОСНОВЫ ТЕОРИИ ПОДОБИЯИ МОДЕЛИРОВАНИЯ ПРОЦЕССОВ
6.1. Дифференциальные уравнения теплообмена
6.3. Моделирование теплоотдачи
6.4. Физические особенности процесса теплоотдачи
7. ТЕПЛООТДАЧА В ОДНОФАЗНОЙ СРЕДЕ
7.1. Теплоотдача при свободном движении жидкости
7.2. Теплоотдача при продольном омывании поверхности вынужденным потоком жидкости
7.3. Теплоотдача при вынужденном течении жидкости в трубах и каналах
7.4. Теплоотдача при поперечном обтекании труб
8. ТЕПЛООТДАЧА ПРИ ФАЗОВЫХ ПРЕВРАЩЕНИЯХ
8.2. Теплоотдача при конденсации
9.1. Классификация теплообменников
при tс=94,5; Prж с=1,845.
Теплоту парообразования берем из табл.9 приложения, при t=100оС r=2257,2 кДж/кг.
Рассчитываем
|
Режим течения пленки ламинарно-волновой, тогда
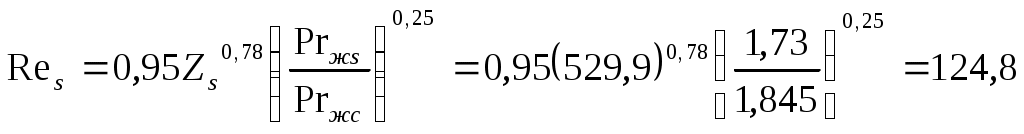 .
.Коэффициент теплоотдачи
Количество пара, которое конденсируется на поверхности трубы за 1с
за 1 час
Задание. Рассчитайте, как изменится и G, кг/ч, если труба будет горизонтальной? Сделайте практические выводы.
9. ТЕПЛООБМЕННЫЕ АППАРАТЫ
9.1. Классификация теплообменников
Теплообменными аппаратами,или теплообменниками называются устройства, предназначенные для передачи тепла от более нагретой жидкости – горячего теплоносителя – к менее нагретому – холодному теплоносителю.
По способу передачи теплоты различают смесительные и поверхностные теплообменники.
В смесительных теплообменниках теплообмен осуществляется путем непосредственного контакта и смешения горячего и холодного теплоносителей. Наиболее простыми и компактными являются смесительные теплообменники, в которых смешиваются теплоносители, не требующие дальнейшего разделения: вода смешивается с паром в подогревателе воды; вода из котельной смешивается с водой, возвращающейся от потребителя в радиаторах отопления.
Используются смесительные теплообменники для легко разделяющихся теплоносителей: газ – жидкость, вода – масло, газ – дисперсный твердый материал.
Поверхностные теплообменные аппараты делятся на регенеративные и рекуперативные. В первых теплота от горячих газов аккумулируется насадкой (металлические шары, листы стали, кирпич), а затем передается нагреваемому газу путем его продувания через горячую насадку (регенеративные воздухоподогреватели, теплообменники для охлаждения запыленных газов).
В рекуперативных аппаратах теплота от горячего теплоносителя передается к холодному через разделяющую их стенку. Наиболее распространены трубчатые теплообменники, в которых один теплоноситель движется в трубах, другой – в межтрубном пространстве (подогреватели, охладители, конденсаторы, испарители).
9.2. Основные уравнения для расчета теплообменников
Тепловой расчет теплообменника может быть конструкторским, целью которого является определение площади поверхности теплообмена, и поверочным, когда при известной поверхности нагрева определяется количество передаваемой теплоты и конечные температуры теплоносителей.
Основными уравнениями для расчета теплообменников являются:
-
уравнение теплового баланса; -
уравнение теплопередачи; -
уравнение массового расхода теплоносителей.
Уравнение теплового баланса при условии отсутствия тепловых потерь имеет вид
| | (9.1) |
где G, кг/с – массовый расход теплоносителя; h, Дж/кг – энтальпия. Здесь и далее индексы 1, 2 относятся соответственно к горячему и холодному теплоносителям, один штрих () и два штриха () – к параметрам на входе в теплообменник и на выходе из него.
При отсутствии кипения или конденсации теплоносителей уравнение теплового баланса можно записать в виде
| | (9.2) |
где
или
| | (9.3) |
где С=G
Из уравнения (9.3) следует, что отношение расходных теплоемкостей обратно пропорционально отношению их изменений температур:
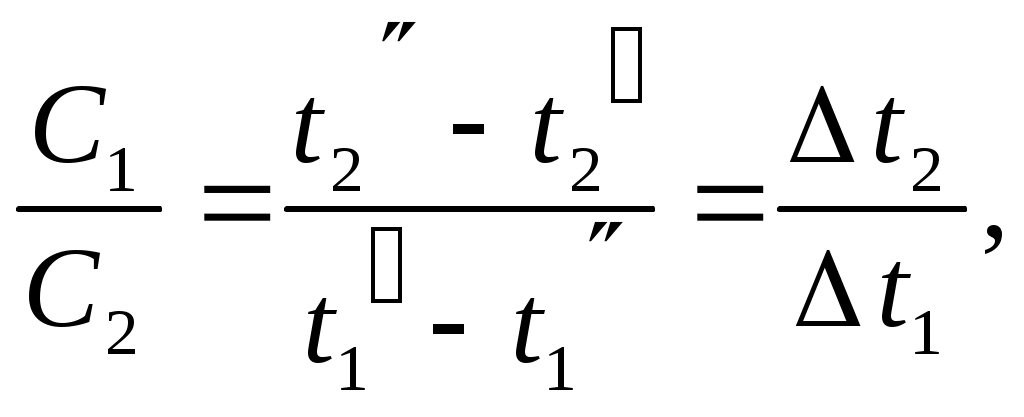 | (9.4) |
Уравнение теплового баланса с учетом тепловых потерь запишется в виде
| | |
где
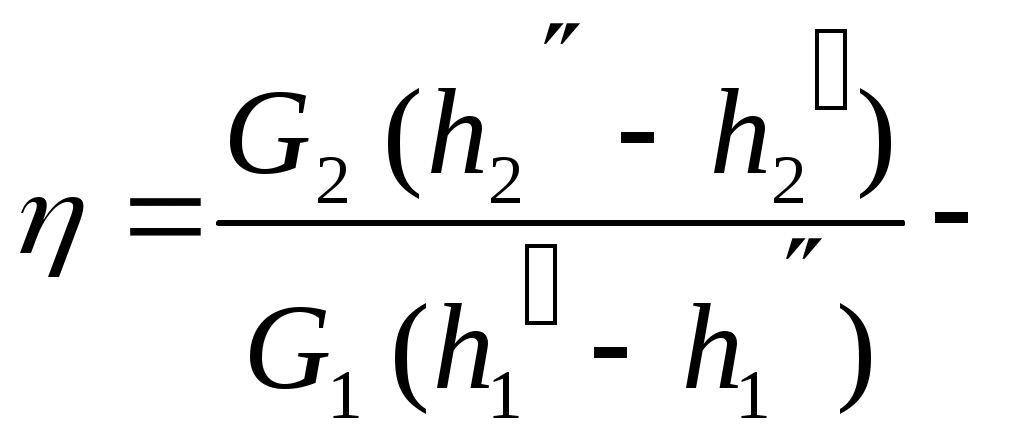 КПД теплообменника, учитывающий потери тепла в окружающую среду.
КПД теплообменника, учитывающий потери тепла в окружающую среду.Эксергетический КПД теплообменника
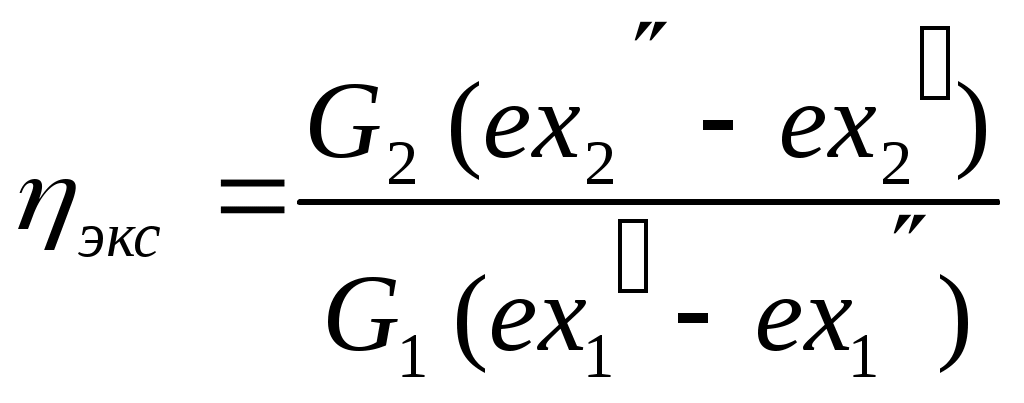 | |
учитывает потери эксергии в составе потерь тепла и потери эксергии от необратимого теплообмена между горячим и холодным теплоносителем при конечной разности средних температур (
Уравнение теплопередачи имеет вид
| | (9.5) |
где
к – коэффициент теплопередачи;
F, м2 – площадь поверхности;
и используется для нахождения площади поверхности теплообмена F.
Если обозначить
| | (9.6) |
где
| | (9.7) |
В рекуперативных теплообменниках для уменьшения термического сопротивления стенка выполняется из материала с хорошей теплопроводностью (меди, латуни, сплавов алюминия, стали), и в этом случае для стенок любой формы (например труб) коэффициент теплопередачи с достаточной точностью рассчитывается по формуле для плоской стенки
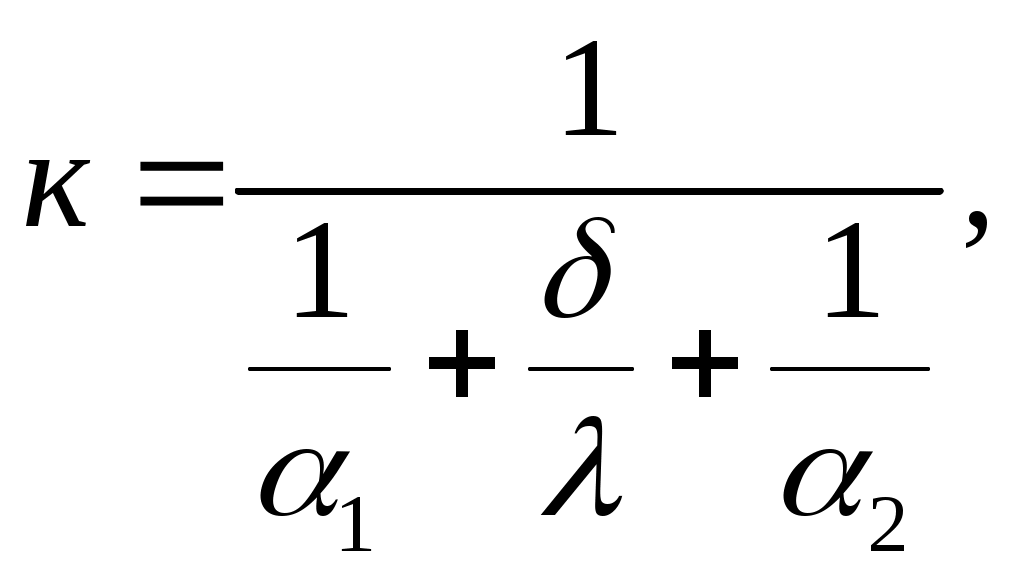 | (9.8) |
где 1, 2, Вт/м2К – средние коэффициенты теплоотдачи между стенкой и теплоносителями; , м, , Вт/мК – толщина и коэффициент теплопроводности стенки.
В рекуперативных теплообменниках в зависимости от направления потоков горячего и холодного теплоносителей различают три основные схемы движения:
1. Если оба теплоносителя движутся параллельно в одном направлении, то схема называется прямотоком.
2. Если теплоносители движутся параллельно, но в противоположных направлениях, то схема движения называется противотоком.
3. Если один теплоноситель движется в направлении, перпендикулярном к направлению движения другого теплоносителя, то схема движения называется перекрестным током.
Кроме указанных, существуют более сложные схемы движения, являющиеся различными комбинациями рассмотренных основных схем.
Н
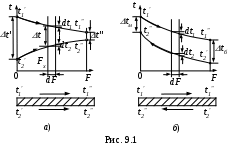
а рис. 9.1 представлены графики изменения температур теплоносителей вдоль поверхности теплообмена F для прямотока (а) и противотока (б).
При прямотоке t=t1-t2 - температурный напор на входе в теплообменник, t=t1-t2 - температурный напор на выходе из теплообменника, t – текущий температурный напор при Fх.
Обратите внимание, что при прямотоке температура холодного теплоносителя на выходе теплообменника (t2) всегда меньше температуры горячего теплоносителя (t1):
| t2< t1. | |
При противотоке t, tм – больший и меньший температурные напоры. Холодный теплоноситель может нагреваться до более высокой температуры, чем t1:
| t2> t1. |
Это дает основание заключить, что противоточная схема предпочтительнее прямоточной.
Получим формулу для расчета среднего температурного напора при прямотоке.
Запишем уравнение теплового баланса и уравнение теплопередачи для элемента поверхности dF (рис.9.1,а):
| d Q=-С1dt1=С2 dt2 , | (9.9) |
| d Q=к(t1- t2) dF. | (9.10) |
Из (9.9) имеем
| |
Разность
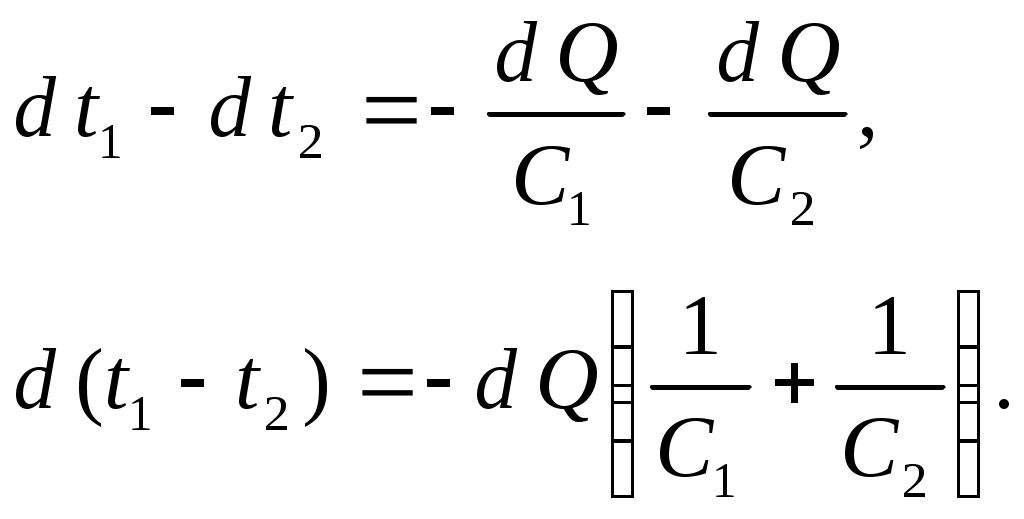 |
Обозначим
| |
тогда
| d (t1- t2)=-т dQ. |
Подставим
| |
в (9.10) и получим
| |
откуда
| | (9.11) |
Проинтегрируем (9.11) от t до текущего температурного напора t и от 0 до Fx (рис. 9.1, а), получим
| | |
| | |
| | (9.12) |
Последняя формула описывает закон изменения текущего температурного напора вдоль поверхности теплообмена.
Проинтегрируем (9.11) от t до t и от 0 до F, где F – площадь поверхности теплообменника.
Получим
| | (9.13) |
| | (9.14) |
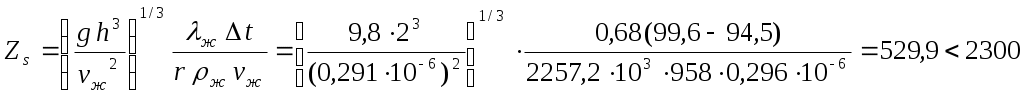 .
.