Файл: Учебное пособие Томск 2001 удк.doc

. Известны: q_v , =const, (рис. 3.2).

Определить: уравнение температурного поля t=f(x), потоки теплоты (Q₁, Q₂), координату максимальной температуры (х₀).

Математическая формулировка задачи включает в себя дифференциальное уравнение температурного поля пластины (3.1), граничные условия третьего рода для поверхностей пластины (3.12), (3.13) и условие максимума температуры при х=х₀ (3.14):

	(3.12)
	(3.13)
	(3.14)

Три уравнения (3.12) – (3.14) необходимы для определения постоянных интегрирования с₁ и с₂ и координаты максимальной температуры х₀.

Решение системы дифференциальных уравнений (3.1), (3.12) – (3.14) дает уравнение температурного поля пластины t=f(x) при несимметричных условиях охлаждения

(3.15)

где



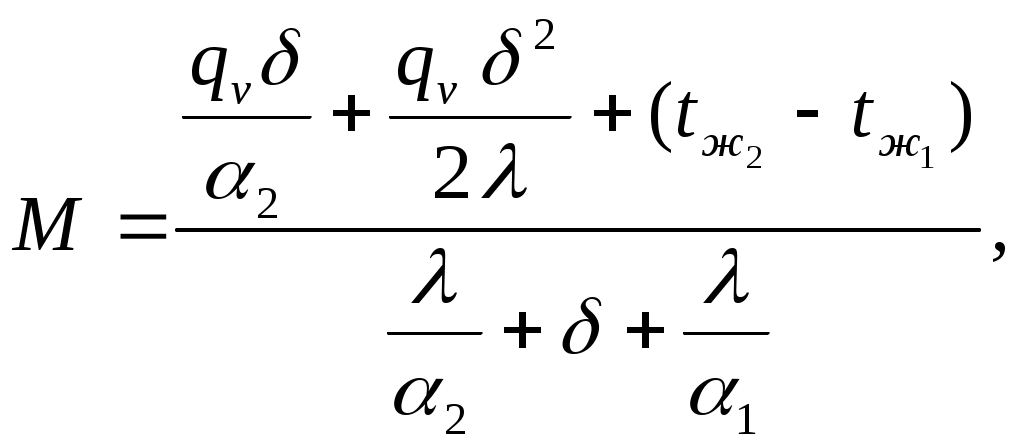
и формулу для расчета координаты максимальной температуры

(3.16)

Уравнение (3.15) – несимметричная парабола (рис. 3.2). Формулы для вычисления температур на поверхностях пластины и максимальной температуры (t_тах) можно получить, если в (3.15) подставить значения х=0, х=, х=х₀ соответственно.

Потоки тепла, рассеиваемые поверхностями пластины

---

, рассчитываются по формулам

(3.17)

,

(3.18)

где F, м² – площадь поверхности пластины; V₁, V₂, м³ – тепловыделяющие объемы.
Несимметричные условия охлаждения (граничные условия первого рода)

Дано: тонкая пластина толщиной . Известны: q_v, =const, (рис. 3.2).

Определить: уравнение температурного поля t=f(x), координату максимальной температуры (х₀).
Математическая формулировка задачи включает в себя дифференциальное уравнение температурного поля пластины (3.1), граничные условия первого рода для поверхностей пластины:

при х=0	(3.19)
при х=δ	(3.20)

и условие максимума температуры (3.14).

Решение системы уравнений (3.1), (3.19), (3.20), (3.14) дает уравнение температурного поля t=f(x) в виде

(3.21)

и формулу для расчета координаты максимальной температуры

(3.22)

Потоки тепла, рассеиваемые поверхностями пластины, рассчитываются по уравнениям (3.17), (3.18).

---

3.2. Теплопроводность однородного цилиндрического стержня

Дано: длинный цилиндрический стержень радиусом r₀ с коэффициентом теплопроводности =const, с объемным тепловыделением q_v находится в среде с температурой t_ж, задан коэффициент теплоотдачи = const (рис. 3.3).

У 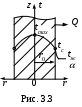словие "длинного" стержня предполагает пренебрежимо малый отток тепла в среду с торцов стержня. Вся теплота отдается в среду только цилиндрической поверхностью стержня. При этом температура цилиндрической поверхности будет одинаковой (t_c) и температура в стержне будет изменяться только по радиусу.

Определить: уравнение температурного поля t=f(x); тепловой поток (Q, Вт), рассеиваемый цилиндрической поверхностью стержня.
Температурное поле цилиндрического стержня описывается дифференциальным уравнением теплопроводности в цилиндрических координатах (1.14). При условиях стационарного режима и постоянства температур t_с и t_ж уравнение (1.14) запишется в виде

(3.23)

Граничные условия третьего рода для цилиндрической поверхности стержня

(3.24)

Условие максимума температуры в центре стержня

(3.25)

Решением уравнения (3.23) является общий интеграл

(3.26)

---

После нахождения постоянных интегрирования с₁и с₂ с помощью условий (3.24) и (3.25) получим уравнение температурного поля цилиндрического стержня t=f(r) в виде

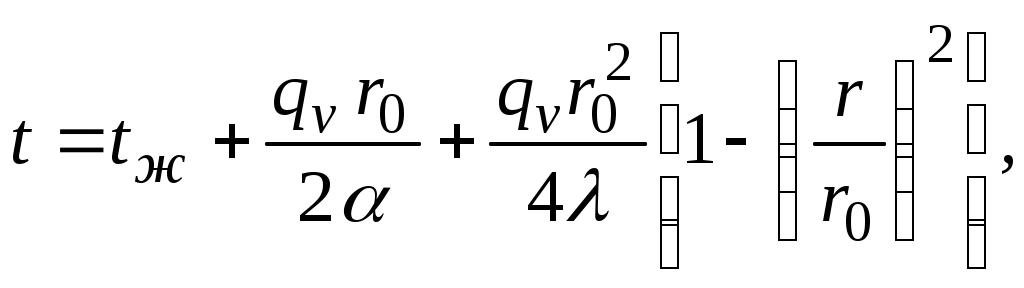(3.27)

где r – текущий радиус.

Уравнение (3.27) – симметричная парабола (рис. 3.3).

Подстановка в (3.27) r = 0, r = r₀ дает расчетные формулы для t_max , t_c:

	(3.28)
	(3.29)

При подстановке (3.29) в (3.27) получим уравнение температурного поля цилиндрического стержня при граничных условиях первого рода

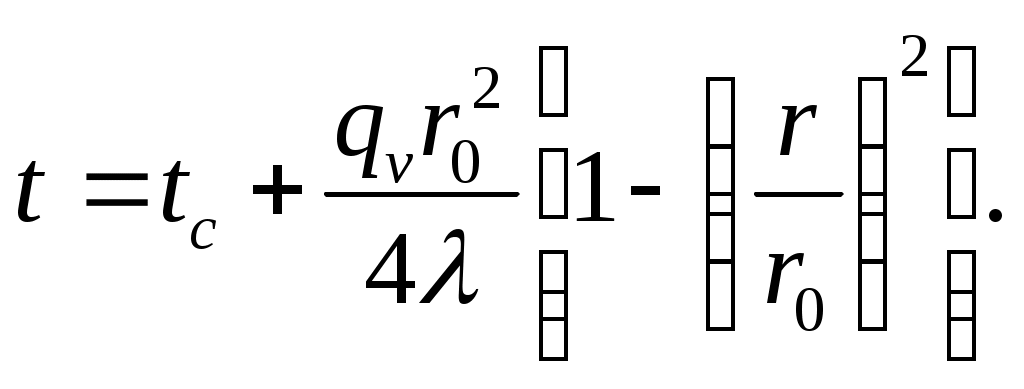(3.30)

Тепловой поток,рассеиваемый цилиндрической поверхностью, можно определить двумя способами:

где F=2 r₀ , м³ – площадь цилиндрической поверхности стержня;
V= r₀² , м³ – объем стержня; , м – длина стержня.

---

3.3. Теплопроводность цилиндрической стенки

Рассматривается цилиндрическая стенка с внутренним тепловыделением q_v при отсутствии теплоотдачи с торцов. Температурное поле такой стенки описывается уравнением (3.23) с общим интегралом (3.26).

Рассмотрим случаи, когда теплоотдающей поверхностью являются:

1. 
   наружная поверхность;
   
2. 
   внутренняя поверхность;
   
3. 
   обе поверхности.
   

Охлаждение только по наружной поверхности (рис. 3.4)




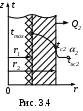
Дано: r₁ ,r₂, , q_v, λ, t_{ж 2}, α₂.

Определить: уравнение температурного поля t=f(r), тепловой поток (Q₂, Вт), рассеиваемый наружной поверхностью.
Для нахождения постоянных интегрирования с₁и с₂ в уравнении (3.26) потребуется два дополнительных условия: граничное условие третьего рода для наружной поверхности стенки

(3.31)

и условие максимума температуры на внутренней поверхности стенки

(3.32)

Решением системы уравнений (3.23), (3.31), (3.32) является уравнение температурного поля t=f(r) в виде

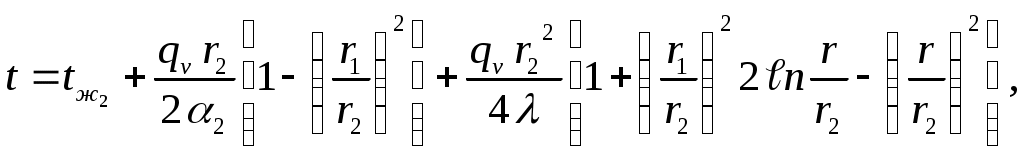(3.33)

где r – текущий радиус.

Расчетные формулы для вычисления максимальной температуры (t_max), температуры наружной поверхности стенки (t_c2) можно получить, если в (3.33) подставить r=r₁, r=r₂ соответственно.

Тепловой поток, рассеиваемый наружной поверхностью стенки,

(3.34)

---