ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 119
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
32. причины нарушения устойчивости массивов грунта
Анализ устойчивости массивов грунта имеет очень большое практическое значение при проектировании земляных сооружений: насыпей, выемок, дамб, земляных плотин, современных больших вскрышных котлованов, имеющих иногда глубину 100м и более, и других подобных сооружений. Главнейшими причинами нарушения устойчивости земляных масс будут: 1 – эрозионные процессы и 2 – нарушение равновесия.
Эрозионные процессы протекают весьма медленно, незаметно; зависят они от внешних метеорологических и физико-геологических условий, а также от свойств поверхности массива грунта и обычно не рассматриваются в механике грунтов.
Нарушение равновесия массивов грунта может происходить внезапно со сползанием значительных масс грунта – такие нарушения равновесия называют оползнями. Это вид нарушений равновесия является наиболее частым и происходит вразличного рода откосах и природных склонах как при увеличении действующих на массив нагрузок, так и при уменьшении внутренних сопротивлений. Оползни бывают: 1)Оползни скольжения 2) оползни вращения 3) оползни разжижения.
36. Динамический модуль упругости
Динамический модуль упругости отражает только упругие свойства материала без влияния ползучести, поскольку при колебаниях образца в нем появляются напряжения, весьма незначительные по величине. По этой причине динамический модуль упругости приблизительно равен начальному модулю упругости, определенному при статических испытаниях, и значительно выше статического модуля деформаций. Разница в величинах динамического и статического модуля обусловлена также тем, что гетерогенность бетона влияет на эти модули по различному механизму. Динамический модуль упругости может быть также определен по скорости распространения импульса ультразвуковой частоты. Значение динамического модуля упругости, определенного по этому методу, зависит от величины коэффициента поперечной деформации, которая обычно точно неизвестна, а изменение величины коэффициента Пуассона от 0,16 до 0,25 приводит к уменьшению величины динамического модуля упругости на 11%. Поэтому определение динамического модуля упругости этим методом обычно не рекомендуется.
37. Распределения напряжений от собственного веса грунта
Мы рассмотрели напряжения, возникающие в массиве грунта от действия внешней нагрузки, приложенной на поверхности. К этим напряжениям прибавятся напряжения от собственного веса грунта, которые принято называть природным давлением. Для однородных грунтов напряжение от собственного веса возрастает по линейному закону и на глубине z от поверхности составит
, где
– удельный вес грунта; z – глубина рассматриваемой точки, а эпюра природных напряжений будет иметь вид треугольника (рис. 3.15, а).
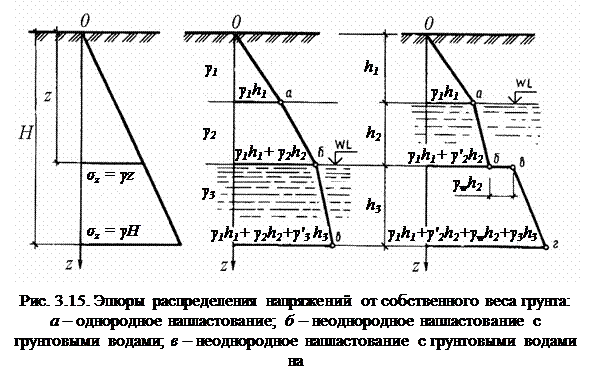
При неоднородном напластовании с горизонтальным залеганием слоев эта эпюра имеет вид ломаной линии (рис. 3.15, б). Наличие уровня грунтовых вод также существенно влияет на вид эпюр напряжений от собственного веса грунта. В этом случае необходимо учитывать взвешивающее действие воды. Для грунтов, находящихся во взвешенном состоянии, удельный вес грунта определяется по формуле
, где
– удельный вес частиц грунта; 
– удельный вес воды; e – коэффициент пористости грунта.В водонепроницаемых грунтах, находящихся ниже уровня грунтовых вод, необходимо дополнительно учитывать гидростатическое давление от столба воды, расположенного над данным слоем (рис. 3.15, в). В связи с этим эпюра давления собственного веса грунта на кровле водоупора имеет скачок, равный
.38. Определения напряжения от собственного веса грунта
Напряжения от собственного веса грунта имеют значение для свеженасыпанных земляных, сооружений, оценки природной уплотненности грунтов и в расчетах осадок оснований фундаментов. При горизонтальной поверхности грунта напряжения от собственного веса будут увеличиваться с глубиной.
Вертикальное напряжение от собственного веса грунта σzg представляет собой вес столба грунта над рассматриваемой точкой с площадью поперечного сечения, равной единице.
При постоянном удельном весе грунта γ по глубине по оси z напряжения σzg определяются по формуле
. (1.1)При слоистом залегании грунтов, обладающих различным удельным весом, или наличии грунтовых вод (рис. 1.1) величина σzg определяется суммированием:
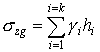. (1.2)Горизонтальные напряжения σyg и σxg также увеличиваются с глубиной и определяются по формуле
, (1.3)где
– коэффициент бокового давления грунта; 
– коэффициент относительных поперечных деформаций, аналогичный коэффициенту Пуассона упругих тел.Коэффициент Пуассона
принимается равным для грунтов: крупнообломочных – 0,27; песков и супесей – 0,30; суглинков – 0,35; глин – 0,42.Вариант задания принимается по последней цифре шифра зачетной книжки студента и соответствующей специальности.
С использованием исходных данных для конкретного варианта строится эпюра напряжений σzg от собственного веса грунта.
39.Принцип линейной деформируемости и деформативные характеристики грунтов
Осадка фундамента есть интегральный эффект напряжений и деформаций, действующих в каждой точке основания от передаваемой фундаментом нагрузки. Иначе говоря, осадка определяется напряженно-деформированным состоянием грунта (НДС), описание которого – важная задача механики грунтов.
Поскольку грунт в основании или в массиве находится в пространственном НДС, для его моделирования применяются приборы трехосного сжатия – стабилометры. По конструкции стабилометры разнообразны, но в общем они позволяют управлять одной группой параметров НДС (например, создавать заданные напряжения
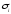и управлять ими) и определять как «отклик» грунта другую (например, замерять деформации 
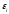).Наиболее распространен гидравлический стабилометр. При испытании цилиндрический образец грунта первоначально подвергается всестороннему (гидростатическому) сжатию напряжениями
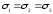. Затем боковые (радиальные) напряжения остаются постоянными 
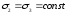, а образец сжимается увеличивающимся вертикальным напряжением 
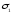с фиксацией вертикальных и горизонтальных деформаци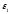й 
и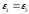 
.При некотором значении
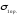грунт разрушается. Зависимость 
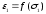и разрушающее напряжение 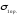зависят от зафиксированного значения 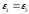, но во всех случаях график зависимости 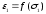имеет тот же вид, что и показанный на рис. 2.1. Таким образом, для образца грунта справедлива та же самая стадийность деформирования.В стадии уплотнения и даже в начале стадии сдвигов зависимость деформаций от напряжений близка к линейной. Это позволяет в указанном интервале связь деформаций и напряжений принять в виде закона Гука:
;
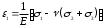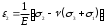; (2.1)
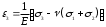.Параметры зависимостей (2.1) в механике грунтов называются: Е – модуль деформации;
– коэффициент поперечной деформации, или коэффициент Пуассона. Это деформативные характеристики грунта. Их смысл выявляется из простого испытания на одноосное сжатие, когда
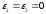и образец грунта сжимается вертикальным напряжением на простейшем прессе. Конечно, так можно испытывать только достаточно прочные связные грунты. При этом из (2.1) получаем: 
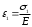и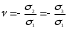 
.Отсюда ясно, чтоЕ характеризует жесткость грунта и измеряется в единицах напряжения (Па, кПа и т.д.), а
– меру деформирования в направлении, перпендикулярном действующему напряжению.Интервал значений
для грунтов составляет обычно 0,1…0,5. Значения модуля деформации оказывают определяющее влияние на рассчитываемую осадку сооружений. Поэтому их определение имеет большее значение, а значения ν на практике часто принимают по справочным данным в зависимости от вида и состояния грунта.Положение о применимости зависимостей (2.1) в механике грунтов характеризуется как «Принцип линейной деформируемости грунтов». При этом напряжения в грунте должны быть достаточно далеки от разрушающих, т.е. грунт должен работать в стадии уплотнения – начале стадии сдвигов.
40. динамические воздействия на грунт.
Всякое изменение нагрузки действующей на сооружения и основания, сообщает им ускорения, приводящие к появлению колебаний. Последние распространяются от точки приложения нагрузки в виде волн, уносящих с собой от источника колебаний энергию, и передают её от точки к точке среды, в которой волны движутся. При поглощении или отражении телом волн они оказывают на него динамическое воздействие - передают ему силовые импульсы. Амплитуды и частоты колебаний, скорости их распространения и затухания со временем и с расстоянием от источника воздействия зависят не только от характера нагружения, но и от физико-механических свойств среды.
Перемещения при колебаниях и волновых воздействиях сооружений и их оснований и возникающие в них динамические силы и напряжения могут вызывать деформации и повреждения, приводить к значительным и неравномерным осадкам и кренам фундаментов. Удары и колебания, особенно при сильных взрывах и землетрясениях, могут настолько понижать прочность грунтов, что значительные их массы теряют устойчивость и обрушиваются, а водонасыщенные пески могут переходить в разжиженное состояние и растекаться.